
- •Элементы векторной алгебры и аналитической геометрии
- •Введение
- •1. Элементы векторной алгебры в трехмерном пространстве
- •1.1. Векторы. Основные определения и линейные операции
- •1.2. Скалярное произведение векторов
- •1.3. Векторное произведение векторов
- •1.4. Смешанное произведение векторов
- •2. Элементы аналитической геометрии
- •2.1. Плоскость в пространстве
- •2.2. Прямая в пространстве
- •2.3. Взаимное расположение плоскостей и прямых в пространстве
- •2.4 Кривые на плоскости и в пространстве
- •2.5 Поверхности второго порядка
- •Литература
2.3. Взаимное расположение плоскостей и прямых в пространстве
Две плоскости могут быть параллельны, могут совпадать или пересекаться. Положение плоскостей по отношению друг к другу в первую очередь определяется их нормалями. Если нормали параллельны, то плоскости параллельны или совпадают. В противном случае плоскости пересекаются и можно определить угол между плоскостями. Углом между плоскостями называется острый угол, образованный в сечении, перпендикулярном линии пересечения плоскостей. Этот угол равен "острому углу" между нормалями3 (рис. 11), который можно определить, используя формулу (17).
|
Рис. 11
Пример 19. Даны две плоскости:
 и
и
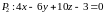 .
.
Доказать, что плоскости параллельны и найти расстояние между ними.
Решение.
Нормали к плоскостям
 и
и
 ,
соответственно,
,
соответственно,
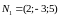 и
и
 Для них верна
пропорциональность координат:
Для них верна
пропорциональность координат:

следовательно, плоскости параллельны или совпадают. Система

не имеет решений [4], то есть плоскости не имеют общих точек, и значит, они параллельны.
Расстояние между двумя
плоскостями равно длине отрезка между
ними, перпендикулярного этим плоскостям.
Достаточно взять на одной из плоскостей
точку и найти расстояние от этой точки
до другой плоскости. Точка
 .
Применив формулу (31), получаем
.
Применив формулу (31), получаем
|
|
◄ |
Пример 20. Даны две плоскости:
и
 .
.
Проверить, что плоскости совпадают.
Решение. Проверив, как и в примере 19, параллельность нормалей, переходим к системе

Эта система имеет множество решений [4], следовательно, плоскости совпадают.
Пример 21. Даны две плоскости:
и
 .
.
Убедиться, что плоскости пересекаются и найти угол между ними.
Решение.
Нормали к плоскостям
 .
Так как
.
Так как
 ,
то плоскости не параллельны. Найдем
угол между плоскостями. С учетом того,
что нас интересует "острый угол"
в числителе формулы (17) необходимо
поставить модуль (см. сноску на стр.21).
Итак,
,
то плоскости не параллельны. Найдем
угол между плоскостями. С учетом того,
что нас интересует "острый угол"
в числителе формулы (17) необходимо
поставить модуль (см. сноску на стр.21).
Итак,
|
|
◄ |
Две прямые могут быть параллельны (рис. 12а), могут совпадать, пересекаться (рис. 12б), или скрещиваться (рис. 12в). Углом между непараллельными прямыми называется "острый угол", образованный их направляющими векторами. Две непараллельные прямые называются скрещивающимися (рис. 12в), если у них нет общих точек. Для параллельных или скрещивающихся прямых можно найти расстояние между прямыми.
|
|
|
12а |
12б |
12в |
Рис. 12
Пример 22. Проверить, что прямые
|
и |
|
совпадают.
Решение. Для прямой
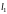 в примере 18 мы получили уравнения в
параметрической форме
в примере 18 мы получили уравнения в
параметрической форме 
Направляющие векторы прямых
 и
и
 :
:
 ,
,
 ,
соответственно. Координаты этих векторов,
очевидно, пропорциональны.
,
соответственно. Координаты этих векторов,
очевидно, пропорциональны.
Следовательно, прямые
параллельны или совпадают. Для
окончательного решения достаточно
взять точку на одной прямой и подставить
ее координаты в уравнения другой прямой.
Проверим точку
 ,
подставив ее координаты в уравнения
прямой
,
подставив ее координаты в уравнения
прямой
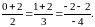
Все равенства выполнены, следовательно, прямые совпадают. |
◄ |
Пример 23. Проверить, что прямые
|
и |
|
параллельны и найти расстояние между ними.
Решение.
Прямые параллельны, если их направляющие
векторы коллинеарны, и прямые не имеют
общих точек. Направляющий вектор прямой
:
(пример
22), для
:
.
Координаты этих векторов пропорциональны.
Подставим координаты точки
 в
уравнения прямой
:
в
уравнения прямой
:

Равенства не выполнены, следовательно, прямые не имеют общих точек, значит, параллельны.
Определим расстояние между ними. Расстояние между двумя параллельными прямыми равно длине перпендикуляра, заключенного между ними (рис. 13).
D
C
B
H
A |
Рис. 13
 перпендикуляра равна высоте параллелограмма,
построенного на векторах
перпендикуляра равна высоте параллелограмма,
построенного на векторах и
и
 вне зависимости от того, как взяты точки
вне зависимости от того, как взяты точки
 на
прямых (см. рис.13). Возьмем точки:
на
прямых (см. рис.13). Возьмем точки:
 ,
,
 .
.
Площадь параллелограмма
 вычислим через векторное произведение
(см. пример 7). Найдем векторы:
вычислим через векторное произведение
(см. пример 7). Найдем векторы:
 ,
,
 ,
,
тогда

Следовательно, |
|
◄ |
Пример 24. Проверить, что прямые
|
и |
|
пересекаются. Найти угол между прямыми.
Решение. Прямые пересекаются, если имеют одну общую точку. Это можно выяснить, решив систему уравнений

Подобное изложение методов решения
таких систем приведено в
методических указаниях по линейной
алгебре [5]. Например, запрограммировав
в EXCEL метод Гаусса, получим,
что эта система имеет единственное
решение
 .
Следовательно, прямые пересекаются.
Листинг вычислений представлен на рис.
14.
.
Следовательно, прямые пересекаются.
Листинг вычислений представлен на рис.
14.

Рис. 14
Направляющие векторы вычислим как в примере 18.

Вычислим косинус "острого угла" между направляющими векторами (17)

Теперь вычисляем угол:
|
|
◄ |
Пример 25. Проверить, что прямые
|
и |
|
пересекаются и найти точку пересечения. Написать уравнение плоскости, где они лежат.
Решение. Прямые
и
проходят через точки
 и
и
 соответственно
и имеют направляющие векторы
соответственно
и имеют направляющие векторы
 и
и
 Прямые не параллельны, так как векторы
Прямые не параллельны, так как векторы
 и
и
 не коллинеарны. Они лежат в одной
плоскости и, следовательно, пересекаются,
если смешанное произведение
не коллинеарны. Они лежат в одной
плоскости и, следовательно, пересекаются,
если смешанное произведение
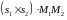 равно нулю, т.е. выполняется условие
(25). Здесь вектор
имеет начало и конец в точках
и
равно нулю, т.е. выполняется условие
(25). Здесь вектор
имеет начало и конец в точках
и
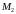 .
По формуле (24)
.
По формуле (24)
 .
.
Вычисляя определитель (см.[5] ), получим, что он равен нулю.
Перепишем уравнения прямой в параметрической форме:
 .
.
Подставим их в уравнения
прямой
и найдем значения параметра
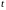 ,
соответствующее точке пересечения.
Получим, что
,
соответствующее точке пересечения.
Получим, что
 .
.
Отсюда
 ,
и координаты точки пересечения
:
,
и координаты точки пересечения
:

Приведем идею другого решения. Переписав уравнения прямых и в параметрической форме, получим систему из 6 линейных уравнений с пятью неизвестными. Оказывается, ранг этой системы равен 5 (см.[5] ), и методом Гаусса можно найти ее единственное решение. Рекомендуем сделать это самостоятельно.
Уравнение плоскости получим, используя формулу (30):
 .
.
Окончательно,
|
|
◄ |
Пример 26. Написать уравнение плоскости, проходящей через две пересекающиеся прямые из примера 24:
|
и |
|
Решение. В примере 24 доказано пересечение
прямых и найдена точка пересечения
 .
Для написания уравнения плоскости
найдем еще по точке на каждой прямой.
Для этого решим две системы, задающие
прямые. Каждая из систем имеет множество
решений. Нас устраивает любое решение
(кроме точки
).
Решая системы, одному из неизвестных
придаем произвольное значение. Решаем
первую систему
.
Для написания уравнения плоскости
найдем еще по точке на каждой прямой.
Для этого решим две системы, задающие
прямые. Каждая из систем имеет множество
решений. Нас устраивает любое решение
(кроме точки
).
Решая системы, одному из неизвестных
придаем произвольное значение. Решаем
первую систему

Пусть
.
Тогда из системы
 получаем
получаем
 .
То есть, точка
.
То есть, точка
 .
Аналогично, положив, например,
.
Аналогично, положив, например, и, решая вторую систему, получаем
и, решая вторую систему, получаем
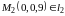 .
.
В результате имеем три точки, не лежащие на одной прямой, и можем записать уравнение плоскости, проходящей через три точки по формуле (29):


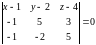 .
.
Раскрывая определитель по первой строке, получаем
 .
.
Раскрывая скобки, получаем уравнение плоскости
|
|
◄ |
Пример 27. Проверить, что прямые
|
и |
|
являются скрещивающимися. Найти угол и расстояние между прямыми.
Решение. Направляющие
векторы прямых
(пример
22) и
 – не коллинеарны. Значит, прямые либо
пересекаются, либо скрещиваются. Общая
точка, если она существует, должна
удовлетворять системе уравнений
– не коллинеарны. Значит, прямые либо
пересекаются, либо скрещиваются. Общая
точка, если она существует, должна
удовлетворять системе уравнений

Записав прямую в параметрической форме
 ,
,
подставим
 в первые два уравнения системы:
в первые два уравнения системы:
|
|
|
Система не имеет решений, следовательно, данные прямые скрещиваются.
|
|
Рис. 15 |
Рис. 16 |
Углом между двумя скрещивающимися прямыми называется острый угол, который получается при параллельном перемещении одной из прямых до пересечения с другой прямой (рис. 15). Следовательно, он равен "острому углу" между направляющими векторами, косинус которого находим по формуле (17), а затем сам угол
 или
или
 .
.
Расстояние
между двумя скрещивающимися прямыми
равно длине перпендикуляра,
проведенного к обеим прямым. На рисунке
16 концы перпендикуляра обозначены
буквами
 и
и
 .
.
Возьмем по одной точке на
каждой прямой. Длина перпендикуляра
равна модулю проекции вектора
 ,
на любой вектор, параллельный вектору
,
на любой вектор, параллельный вектору
 при
произвольном выборе точек
при
произвольном выборе точек
 и
и на прямых (рис. 16). Так как
на прямых (рис. 16). Так как
 ,
то
,
то
 коллинеарен векторному произведению
коллинеарен векторному произведению
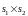 ,
,

Для определения длины перпендикуляра
найдем вектор
и модуль его проекции на вектор
 .
.
Точка
 (пример 18),
(пример 18),
 ,
вектор
,
вектор
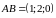 .
Расстояние вычисляем по формуле (18):
.
Расстояние вычисляем по формуле (18):
|
|
◄ |
Плоскость и прямая могут быть параллельны (рис. 17а), могут пересекаться (рис. 17б). Прямая может также лежать в плоскости (рис. 17в). Это определяется, в первую очередь, взаимным расположением нормали плоскости и направляющего вектора прямой. Если эти векторы перпендикулярны, то плоскость и прямая параллельны или прямая лежит в плоскости. В противном случае прямая и плоскость пересекаются и можно определить угол между прямой и плоскостью. Углом между прямой и плоскостью называется острый угол между прямой и ее проекцией на плоскость (угол на рисунке 17б).
|
|
|
17а |
17б |
17в |
Рис. 17
Пример 28. Заданы
плоскость
 и прямая
и прямая
 .
Доказать, что прямая принадлежит
плоскости.
.
Доказать, что прямая принадлежит
плоскости.
Решение. Если две точки прямой принадлежат плоскости, то прямая принадлежит плоскости. Возьмем две точки на прямой. Для этого уравнения прямой удобнее записать в параметрическом виде:
 .
.
Взяв
 и
и
 ,
получаем две точки, принадлежащие
прямой:
,
получаем две точки, принадлежащие
прямой:
 и
и
 соответственно. Проверим, принадлежат
ли точки плоскости:
соответственно. Проверим, принадлежат
ли точки плоскости:
 ,
,

Следовательно, прямая принадлежит плоскости. |
◄ |
Пример 29. Заданы
плоскость
и прямая
 .
Доказать, что прямая параллельна
плоскости. Найти расстояние от прямой
до плоскости.
.
Доказать, что прямая параллельна
плоскости. Найти расстояние от прямой
до плоскости.
Решение.
Вектор нормали
 ,
направляющий вектор прямой
,
направляющий вектор прямой
 .
Вычисляем скалярное произведение (19)
.
Вычисляем скалярное произведение (19)
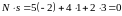 .
.
Следовательно, прямая либо принадлежит плоскости, либо параллельна ей.
Возьмем на прямой точку
 .
Подставив ее координаты в уравнение
плоскости, получаем
.
Подставив ее координаты в уравнение
плоскости, получаем

Следовательно, прямая параллельна плоскости.
Найдем расстояние от прямой до плоскости. Так как прямая параллельна плоскости, то все точки прямой равноудалены от плоскости, и достаточно найти расстояние любой точки прямой до плоскости. Возьмем на прямой точку , и вычислим расстояние по формуле (31)
|
|
◄ |
Пример 30. Показать,
что прямая
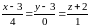 пересекает плоскость
пересекает плоскость Найти точку пересечения и определить
угол между прямой и плоскостью.
Найти точку пересечения и определить
угол между прямой и плоскостью.
Решение.
Вычислим скалярное произведение вектора
нормали к плоскости
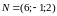 и направляющего вектора прямой
и направляющего вектора прямой
 :
:

Следовательно, прямая пересекает плоскость. Для нахождения точки пересечения запишем уравнения прямой в параметрической форме и подставим их в уравнение плоскости:

Получив значение
 ,
находим координаты точки пересечения
,
находим координаты точки пересечения

Напомним, что угол между прямой и плоскостью – острый угол между прямой и ее проекцией на плоскость (рис. 18)
|
Рис. 18 |
Так как прямая, ее проекция
и перпендикуляр к плоскости, опущенный
из какой-либо точки прямой на плоскость,
образуют прямоугольный треугольник,
то угол
между прямой и плоскостью равен
 , где
– угол между прямой и перпендикуляром
к плоскости, а
, где
– угол между прямой и перпендикуляром
к плоскости, а
 .
.
Угол – это "острый угол" между направляющим вектором прямой и нормалью к плоскости . Нормаль к плоскости , направляющий вектор прямой . Окончательно из формулы (17) получаем
 ,
,
|
◄ |
Пример 31. Написать уравнение плоскости, проходящей через две параллельные прямые:
|
и |
|
Решение. Через две параллельные прямые можно провести плоскость, и при том только одну. Для этого можно взять две точки на одной прямой, одну на другой и записать уравнение плоскости, проходящей через три точки (29). Параллельность прямых доказана в примере 23. Выбрав три точки:
 ,
,
запишем уравнение плоскости, проходящей через три точки


|
|
◄ |
Пример 32. Написать уравнение плоскости, проходящей через пересекающиеся прямые:
|
и |
|
Решение. В примере 24 показано, что заданные прямые пересекаются. Через пересекающиеся прямые можно провести плоскость, и при том только одну. Сведем решение к решению примера 13. Направляющие векторы прямых, параллельные искомой плоскости, найдены в примере 24. Точку, принадлежащую плоскости, можно взять на любой прямой, в том числе и точку пересечения (пример 24). Получаем


|
|
◄ |
Решить пример можно и другим способом. Надо взять на одной прямой две точки, на другой одну точку и записать уравнение плоскости, проходящей через три точки (29). Рекомендуем это проделать самостоятельно и сравнить ответы.
Пример 33. Написать уравнения
двух параллельных плоскостей, одна из
которых проходит через прямую

а другая – через прямую 
Решение.
Заданные прямые являются скрещивающимися
(пример 27). Следовательно, существует
единственная пара параллельных
плоскостей, в которых лежат эти прямые.
Направляющие векторы прямых параллельны
каждой из плоскостей. Вектор нормали к
плоскостям
 .
Осталось на каждой прямой взять по точке
и воспользоваться формулой (27).
.
Осталось на каждой прямой взять по точке
и воспользоваться формулой (27).
Возьмем точку , получим уравнение первой плоскости:

Взяв точку , аналогично получаем уравнение для другой плоскости
|
|
◄ |
Пример 34.
Найти точку
 симметричную
точке
симметричную
точке
 относительно
плоскости
относительно
плоскости
 .
.
Решение. Две точки симметричны относительно плоскости, если они лежат на одной прямой, перпендикулярной плоскости, и находятся на одинаковом расстоянии от плоскости. Нормаль к плоскости является направляющим вектором прямой, перпендикулярной плоскости. Уравнения
 ,
,
задают прямую, перпендикулярную плоскости, и проходящую через точку . Найдем значение параметра для точки – точки пересечения этой прямой с плоскостью:

Для точки значение параметра . Так как точки и находятся на одинаковом расстоянии от точки , то для искомой точки Значение параметра .
Откуда находим координаты
искомой точки:
|
◄ |
Пример 35.
Проверить, что точка
 не лежит на прямой
не лежит на прямой
 .
Написать уравнение плоскости, какой
принадлежат эти прямая и точка.
.
Написать уравнение плоскости, какой
принадлежат эти прямая и точка.
Решение. Подставляя
координаты заданной точки в уравнения
прямой, получаем
 .
Следовательно, точка
не
лежит на прямой. По аксиоме стереометрии
через прямую и точку, не лежащую на
прямой, можно провести плоскость и
только одну (рис. 19).
.
Следовательно, точка
не
лежит на прямой. По аксиоме стереометрии
через прямую и точку, не лежащую на
прямой, можно провести плоскость и
только одну (рис. 19).
. |
Рис. 19 |
Возьмем на прямой точку
 и, соединив ее с точкой
,
получим вектор
и, соединив ее с точкой
,
получим вектор .
Направляющий вектор прямой
.
Направляющий вектор прямой
 .
.
Векторы
 параллельны плоскости. По формуле (30)
записываем
параллельны плоскости. По формуле (30)
записываем
 .
.
Вычисляя определитель, окончательно получаем
|
|
◄ |
Другой вариант решения задачи: взять на прямой две точки и воспользоваться формулой 29. Рекомендуем читателям проделать вычисления самостоятельно.




















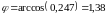 ,
или
,
или  .
.





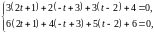









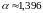 радиан или, переводя в
градусную меру,
радиан или, переводя в
градусную меру,
 .
.


 .
.

