
- •Элементы векторной алгебры и аналитической геометрии
- •Введение
- •1. Элементы векторной алгебры в трехмерном пространстве
- •1.1. Векторы. Основные определения и линейные операции
- •1.2. Скалярное произведение векторов
- •1.3. Векторное произведение векторов
- •1.4. Смешанное произведение векторов
- •2. Элементы аналитической геометрии
- •2.1. Плоскость в пространстве
- •2.2. Прямая в пространстве
- •2.3. Взаимное расположение плоскостей и прямых в пространстве
- •2.4 Кривые на плоскости и в пространстве
- •2.5 Поверхности второго порядка
- •Литература
2.2. Прямая в пространстве
Пусть заданы вектор
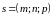 ,
параллельный прямой, и точка
,
принадлежащая этой прямой. Для любой
точки
,
лежащей на прямой, вектор
параллелен вектору
.
По условию параллельности двух векторов
(11)
,
параллельный прямой, и точка
,
принадлежащая этой прямой. Для любой
точки
,
лежащей на прямой, вектор
параллелен вектору
.
По условию параллельности двух векторов
(11)
|
|
(32) |
Уравнения (32) называются
каноническими
уравнениями прямой,
а вектор
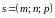 – направляющим
вектором прямой.
– направляющим
вектором прямой.
В канонических уравнениях
одно или два из чисел
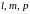 могут оказаться равными нулю. Обращение
в нуль знаменателя означает обращение
в нуль и соответствующего числителя.
могут оказаться равными нулю. Обращение
в нуль знаменателя означает обращение
в нуль и соответствующего числителя.
Вводя параметр
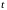 ,
систему уравнений (32) можно переписать
в виде
,
систему уравнений (32) можно переписать
в виде
|
|
(33) |
Уравнения (33) называются параметрическими уравнениями прямой. Из параметрических уравнений прямой при необходимости можно получать, задавая разные значения параметра, любое количество точек, принадлежащих прямой.
Для получения уравнений
прямой, проходящей через две заданные
точки
 и
и
 достаточно в качестве направляющего
вектора взять вектор
достаточно в качестве направляющего
вектора взять вектор
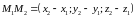 :
:
|
|
(34) |
Прямую в пространстве можно определить и как пересечение двух различных и не параллельных плоскостей
|
|
(35) |
Так как плоскости не параллельны и не совпадают, то нормали к плоскостям не коллинеарны, и нарушается хотя бы одна из пропорций
 .
.
Уравнения (35) называются общими уравнениями прямой в пространстве.
Пример 15. Написать
уравнения прямой, проходящей через
точку
 и параллельной вектору
и параллельной вектору
 .
Проверить проходит ли эта прямая через
точку
.
Проверить проходит ли эта прямая через
точку
 .
.
Решение. По формуле (32) записываем уравнения прямой
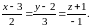
Для проверки, принадлежит ли
точка
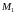 прямой,
подставим ее координаты в полученные
уравнения
прямой,
подставим ее координаты в полученные
уравнения

Равенства верны, следовательно,
точка
|
◄ |
Пример 16.
Написать уравнения прямой, проходящей
через точку
и середину отрезка
,
где
 .
.
Решение.
Определим координаты точки
 – середины отрезка
по формулам (13)
– середины отрезка
по формулам (13)

и запишем уравнения прямой,
проходящей через две точки
и
 (34)
(34)
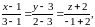
|
|
◄ |
Пример 17. Написать
уравнения прямой, проходящей через
начало координат и параллельной прямой
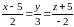 .
.
Решение.
Если две прямые параллельны, то они
имеют одинаковые направляющие векторы.
По формуле (32), с учетом того, что точка
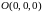 принадлежит
искомой прямой, записываем уравнения
прямой в канонической форме
принадлежит
искомой прямой, записываем уравнения
прямой в канонической форме
|
|
◄ |
Пример 18. Прямая задана как пересечение двух плоскостей
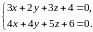
Записать уравнения прямой в канонической и параметрической формах.
Решение.
Отметим, что нормали плоскостей:
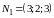 и
и
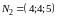 – не коллинеарны, следовательно, такая
прямая существует. Для записи прямой в
канонической (или параметрической)
форме необходимо иметь направляющий
вектор
– не коллинеарны, следовательно, такая
прямая существует. Для записи прямой в
канонической (или параметрической)
форме необходимо иметь направляющий
вектор
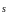 и какую-либо точку
на прямой. Так как линия пересечения
принадлежит каждой из плоскостей, то
она перпендикулярна их нормалям.
Следовательно, за направляющий вектор
прямой можно взять векторное произведение
нормалей
и какую-либо точку
на прямой. Так как линия пересечения
принадлежит каждой из плоскостей, то
она перпендикулярна их нормалям.
Следовательно, за направляющий вектор
прямой можно взять векторное произведение
нормалей
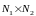 .
.
Определим этот вектор по формуле (22)

Точку на прямой найдем, получив какое-нибудь решение системы
Система имеет множество
решений [4], но нам подходит любое из них.
Положим
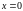 .
Для определения других координат
получаем систему
.
Для определения других координат
получаем систему
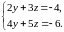 Откуда следует, что
Откуда следует, что
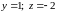 .
Следовательно, точка
.
Следовательно, точка
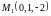 лежит
на прямой.
лежит
на прямой.
Записываем уравнения прямой в канонической (32) и параметрической (33) формах:
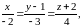
|
|
◄ |



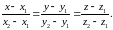

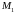 принадлежит прямой.
принадлежит прямой.

