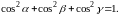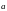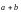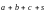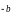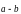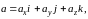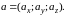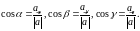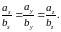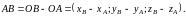А. Б. Алексеев, А.Ф. Филиппова
Элементы векторной алгебры и аналитической геометрии
Методические указания
СПбГУТ
2018
Рецензент
Рекомендовано к печати
редакционно-издательским советом СПбГУТ
Алексеев А. Б.
Элементы векторной алгебры и аналитической геометрии : методические указания / А. Б. Алексеев, А.Ф. Филиппова, – СПб,: Издательство СПбГУТ,2018. – 42 с.
Даны основные положения векторной алгебры в применении к аналитической геометрии, необходимые для успешного освоения других разделов математики и ее приложения к техническим дисциплинам.
Приведена необходимая литература.
Предназначено для студентов I курса всех специальностей.
© А. Б. Алексеев, А.Ф. Филиппова.,2018
©Федеральное государственное
образовательное
бюджетное учреждение высшего
профессионального
образования «Санкт-Петербургский
государственный
университет телекоммуникаций
им. проф. М.А. Бонч-Бруевича», 2018
Введение
Данное пособие дает возможность студентам ознакомиться с основами векторной алгебры и аналитической геометрии в трехмерном пространстве и состоит из двух соответствующих разделов. Оно предназначено студентам 1-го курса, помогает научиться решать задачи и может быть полезно всем, кого интересует достаточно компактное изложение материала.
В каждом параграфе изложены теоретические сведения и приведены формулы, необходимые для решения задач, а также разобраны примеры, иллюстрирующие применение этих формул.
Решение многих задач можно (и рекомендуется) проводить различными способами. Ряд задач требует вычислений, и студентам предлагается обращаться к использованию цифрового процессора EXCEL, для чего указаны стандартные функции EXCEL [4,6].
Нумерация формул и рисунков в пособии сквозная. Ключевые слова в определениях и формулировках утверждений выделены курсивом.
В качестве дополнительных задачников и учебников с подробным изложением материала рекомендуем [1-3].
Авторы выражают благодарность А.О. Жарановой за помощь в оформлении рисунков
1. Элементы векторной алгебры в трехмерном пространстве
1.1. Векторы. Основные определения и линейные операции
Вектором в трехмерном пространстве называется направленный отрезок.
|
Рис. 1
Вектор обозначается либо
двумя буквами – своим началом и концом
–
,
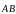либо одной малой буквой
со стрелкой.
Длина этого отрезка называется
модулем
(длиной) вектора и
обозначается
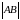или, соответственно,
.
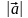В векторной алгебре рассматриваются
свободные векторы, то есть два вектора
равны, если их можно совместить благодаря
параллельному переносу.
Направление
вектора рассматривается
либо относительно других векторов, либо
относительно системы координат. Углы,
которые образует вектор с осями декартовой
системы координат, будем обозначать
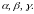Так как эти углы могут меняться только
в пределах от 0 до
(углы измерены в радианах, что и будем
считать в дальнейшем), то между углами
и их косинусами есть взаимно однозначное
соответствие. Поэтому
называются направляющими
косинусами вектора.
Для них выполняется тождество
|
|
(1) |
Если начало и конец вектора
совпадают, то такой вектор называется
нулевым,
его обозначают
.
Длина нулевого вектора равна нулю, а
направление считается произвольным.
Вектор, длина которого равна
единице, а направление совпадает с
направлением числовой оси, называется
единичным
вектором или ортом
этой оси и обозначается
.
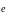Орты
осей декартовой системы координат
обозначаются
.
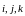Векторы называются коллинеарными
или параллельными
(обозначение: ||),
если они лежат либо на одной прямой,
либо на параллельных прямых, при этом,
если их направления одинаковые, то они
называются сонаправленными
(обозначение:
),
в противном случае – противоположно
направленными(обозначение:
)1.
Векторы называются компланарными, если они параллельны одной плоскости. Два вектора всегда компланарны.
Пусть
заданы два произвольных ненулевых
вектора
и
.
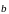Приведем их к общему началу, для этого
отложим от некоторой точки
векторы
и
,
равные, соответственно, заданным векторам
и
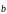(рис.
2).
|
Рис. 2
Углом
между векторами
и
называется
угол
.
Угол между сонаправленными векторами равен 0 радиан, между противоположно направленными – π.
Если
угол между векторами равен
,
то такие векторы называются перпендикулярными
или
ортогональными
(обозначение:
).
Линейными операциями над векторами называются следующие действия: сложение векторов, вычитание векторов и умножение вектора на число.
Суммой
векторов
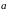и
называется вектор
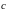(обозначение:
),
построенный с помощью "правила
параллелограмма"
или "правила
треугольника".
Для нескольких векторов используют
"правило
многоугольника".
|
|
|
3а |
3б |
3в |
Рис. 3
По "правилу параллелограмма" совмещаем начальные точки векторов и и достраиваем фигуру до параллелограмма. Вектор, исходящий из общего начала и совпадающий с диагональю, является суммой векторов (рис. 3а). По "правилу треугольника" начало второго вектора совмещаем с концом первого. Суммой векторов является вектор, начало которого совпадает с началом первого, а конец – с концом второго (рис. 3б). На рисунках видно, что результат одинаков. Из "правила треугольника" вытекает "правило многоугольника" для нескольких векторов (рис. 3в).
Произведением
вектора
на число
называется вектор
,
(обозначение:
),
коллинеарный вектору
,
имеющий длину
,
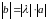то же направление, что и
,
если
,
и противоположное, если
.
Если
,
то вектор
– нулевой вектор.
Вычитание
двух векторов
определяется как операция, обратная
сложению. А именно, вектор
называется
разностью двух векторов
и
(обозначение:
),
если
.
Из "правила треугольника" получаем
вектор, совпадающий с другой диагональю
параллелограмма, (см. рис. 4а).
Вычитание двух векторов
равносильно сложению первого вектора
со вторым, умноженным на минус единицу
(рис. 4б),
.
|
|
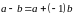4а |
4б |
Рис. 4
Свойства линейных операций:
1)
,
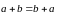2)
,
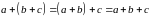3)
,
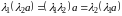4)
,
5)
.
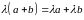Равенство
|
|
(2) |
является условием коллинеарности векторов и .
Проекцией
вектора
на
ось
(обозначение:
)
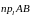называется длина отрезка
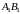(рис. 5), взятая со знаком "+", если
направление вектора
совпадает
с направлением орта оси
(угол
между векторами
и
острый ), и со знаком "-", если эти
направления противоположны (угол между
векторами
и
тупой).
Рис. 5
Для проекции вектора на ось верно соотношение
|
|
(3) |
Также верны свойства:
1)
;
2)
;
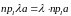3) если вектор
перпендикулярен оси
,
то
;
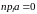4) если вектор
параллелен оси
,
то
,
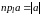если вектор и ось одинаково направлены,
и
,
если они противоположно направлены.
Если направление оси
совпадает с направлением вектора
,
то
,
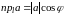где
– угол между векторами
и
.
В этом случае проекция
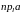называется проекцией
вектора
на
вектор
и обозначается
.
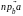Проекции вектора
на оси декартовой системы координат
называются координатами
вектора и обозначаются, соответственно,
.
Любой вектор единственным образом выражается через свои проекции (раскладывается по координатам) и записывается так:
|
|
(4) |
или так:
|
|
(5) |
Нулевой вектор имеет все
координаты, равными нулю:
.
Длина вектора вычисляется по формуле
|
|
(6) |
а направляющие косинусы вектора – по формулам:
|
|
(7) |
На основании единственности представления вектора через координаты справедливы формулы:
|
(8) |
|
(9) |
|
(10) |
Из формул (2), (8), (10) получаем условие коллинеарности векторов и
|
|
(11) |
Вектор, начало которого
совпадает с началом координат, а конец
находится в точке
,
называется радиус-вектором
этой точки (обозначение:
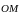или просто
)
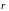и записывается
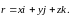
Любой вектор выражается через радиус-векторы, проведенные в точки начала и конца этого вектора:
|
|
(12) |
Пример 1. Даны
точк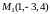и
и
.
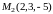Найти координаты вектора
,
его модуль и направляющие косинусы.
Решение. На основании формул (12), (6), (7) записываем:
,
,
|
|
◄ |
Пример 2. Даны
векторы:
,
,
.
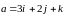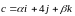Найти
и
,
при которых вектор
и вектор
коллинеарны.
Решение. По формулам (9), (10) и условию коллинеарности (11) получаем
,
.
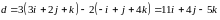Откуда |
|
◄ |
Пример 3. Найти
координаты точки
,
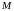делящей отрезок
в
отношении
,
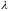считая от конца
.
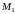Решение. Обозначим
координаты
точки
.
По условию
,
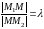а векторы
и
коллинеарны, так как точки
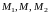лежат на одной прямой. Тогда
=
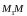и по формуле (10) получаем
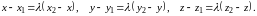
Отсюда находим координаты точки :
|
|
(13) ◄ |
Замечание. Выведенные при решении задачи формулы используются при делении отрезка в заданном отношении.