§9. Индивидуальные задания
Задание 1. Выполнить ортогонализацию в пространстве - квадратично интегрируемых функций на промежутке с весом с помощью процесса Грамма-Шмидта.
1.1.
.
1.2.
.
1.3.
.
1.4.
.
1.5.
.
1.6.
.
1.7.
.
1.8.
.
1.9.
.
1.10.
.
1.11.
.
1.12.
.
1.13.
.
1.14.
.
1.15.
.
1.16.
.
1.17.
.
1.18.
.
1.19.
.
1.20.
.
1.21.
.
1.22.
.
1.23.
.
1.24.
.
1.25.
.
1.26.
.
1.27.
.
1.28.
.
1.29.
.
1.30.
.
Задание
2. В условиях задачи 1, найти расстояние
от функции
до линейной оболочки функций
.
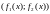Задание 3. Дана функция на промежутке , и заданы точки , , на этом промежутке. Требуется:
а) выписать ряд Фурье для функции в комплексной форме,
б) выписать вещественную форму ряда Фурье функции ,
в) построить график функции и суммы ее ряда Фурье,
г) вычислить значение суммы ряда Фурье в заданных точках,
д) выписать ряд Фурье в амплитудно-фазовой форме,
е) построить амплитудный спектр ряда Фурье, вычислить , , , , ,
ж) выписать равенство Парсеваля.
Задание 4. Для функции из задания №3:
а) выписать ряд Фурье по ортогональной системе функций , , …, ;
б) построить график суммы этого ряда Фурье;
в) выписать равенство Парсеваля.
Задание 5. Для функции из задания №3:
а) выписать ряд Фурье по ортогональной системе функций , , … , , …;
б) построить график суммы этого ряда Фурье.
Задание 6. Требуется написать ряд Фурье и формулу Парсеваля для заданной функции по ортогональной системе собственных функций задачи Штурма-Лиувилля
,
удовлетворяющих краевым условиям:
или периодическим условиям
.
Исходными
данными для индивидуальных заданий
являются: длина промежутка
(полагаем
),
функции
;
числа
.
1.
2.
3.
периодические краевые условия,
4.
5.
6.
периодические краевые условия,
7.
8.
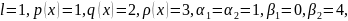
9.
периодические краевые условия,
10.
11.
12.
13.
периодические краевые условия,
14.
15.
периодические краевые условия,
16.
17.
18.
19.
20.
21.
периодические краевые условия,
22.
периодические краевые условия,
23.
24.
периодические краевые условия,
25.
26.
27.
28.
периодические краевые условия,
29.
30.
периодические краевые условия,
