13

9. Несобственные интегралы.

9.1. Несобственный интеграл 1-го рода.

Напомним, что определённый интеграл в основном рассматривался при условии непрерывности функции на замкнутом конечном интервале Здесь мы рассмотрим вопрос определения интеграла для неограниченных интервалов. Такие интегралы называются несобственными интегралами 1-го рода.

Пусть функция непрерывна на интервале Тогда несобственный интеграл определяется равенством

. (9.1)

Если предел (9.1) существует и конечен, то говорят, что интеграл сходится, и предел берется за значение интеграла, а если предел не существует или бесконечен, то говорят, что интеграл расходится.

Аналогично строится определение несобственного интеграла и для других видов неограниченных интервалов. А именно, пусть функция непрерывна на интервале , тогда несобственный интеграл определяется равенством

. (9.2)

Если функция непрерывна на всей оси 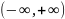, то несобственный интеграл определяется как двойной предел:

(9.3)

где – произвольное число.

Пример 1. Интеграл сходится при и расходится при .

Решение. Для 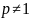найдем первообразную, используя интеграл 1 из таблицы 2, и подставим в формулу Ньютона-Лейбница, тогда

.

Если , то предел конечен и , если , то предел бесконечен и интеграл расходится.

Для первообразная стремится к при . Следовательно, предел бесконечен и интеграл расходится. ◄

Пример 2. Интеграл .

Решение. Воспользуемся первообразной подынтегральной функции, найденной в примере 4 п.7.5. Тогда

. ◄

Замечание. Для несобственного интеграла (9.3) вводится характеристика, которая называется главным значением интеграла. А именно, по определению главным значением интеграла (9.3) называется предел

. (9.4)

Здесь при нахождении предела концы промежутка симметрично уходят на бесконечность. Очевидно, если интеграл (9.3) сходится, то его значение совпадает с главным значением (9.4). Но возможны ситуации, когда интеграл (9.3) расходится, а главное значение (9.4) - конечно.

Пример 3. Интеграл расходится из-за того, что первообразная стремится к при и каждый из интегралов и расходится, но , т.к. для нечетной подынтегральной функции интеграл по симметричному промежутку равен нулю (см. лемму 2 п.8.5). ◄

Для сходящихся несобственных интегралов справедливы все свойства определённого интеграла.

В дальнейшем утверждения будем формулировать для интегралов вида (9.1), подобные утверждения верны и для интегралов (9.2) и (9.3).

Теорема 1. Если функция непрерывна на интервале , то интегралы и сходятся или расходятся одновременно для любого

Доказательство очевидно в силу непрерывности функции на интервале и равенства

■

Теорема 2. Если функция непрерывна на интервале , – ее первообразная, причем существует конечный предел , то интеграл (9.1) сходится и равен .

Доказательство следует из формулы Ньютона-Лейбница. ■

Рассмотрим несобственный интеграл с положительной подынтегральной функцией. В этом случае (см.п.8.2) интеграл с переменным верхним пределом является возрастающей функцией аргумента . Тогда из теоремы о пределе монотонной функции (п.2.3) следует

Лемма. Если существует постоянная такая, что для любого значения 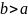выполнено неравенство

,

то интеграл сходится, причем

.

В противном случае интеграл расходится. ■

На эту лемму опирается доказательство теорем, которые называются признаками сходимости.

Теорема 3. Пусть функции и непрерывны на интервале [ . Пусть существует интервал [ , , на котором выполнено неравенство . Тогда:

1) если расходится интеграл , то расходится и интеграл ;

2) если сходится интеграл , то сходится и интеграл .

Доказательство. Докажем второе утверждение, доказательство первого из него следует методом «от противного».

Пусть сходится интеграл . Тогда из теоремы 1 следует, что сходится интеграл , и для любого интеграл . Из условия и (8.10) следует, что

.

Остается сослаться на лемму и теорему 1. ■

Теорема 4. Пусть функции и непрерывны на интервале [ , и

,

где . Тогда интегралы и сходятся или расходятся одновременно.

Доказательство. Зададим число . Для этого числа существует число такое, что из неравенства следует неравенство . Последнее неравенство равносильно системе неравенств:

.

Остается сослаться на теоремы 1 и 3. ■

На практике в качестве функции сравнения удобно использовать степенную функцию. Это следует из примера 1.

Пример 4. Выяснить сходится или расходится интеграл .

Решение. Для очевидна оценка подынтегральной функции:

.

Так как сходится, то сходится и заданный интеграл. ◄

Для произвольной (знакопеременной) непрерывной функции доказано (см. [2]) утверждение: если сходится интеграл , то сходится и интеграл . ■

Это утверждение позволяет ввести два новых понятия для интегралов от функций, которые принимают значения любого знака.

Несобственный интеграл называется абсолютно сходящимся, если сходится интеграл .

Несобственный интеграл называется неабсолютно или условно сходящимся, если он сходится, а интеграл расходится.

Для абсолютно сходящихся интегралов верна теорема, которая является следствием теоремы 3.

Теорема 5. Пусть функции и ( ) непрерывны на интервале [ . Пусть . Тогда, если сходится интеграл , то абсолютно сходится интеграл , причем

. ■

Пример 5. Исследовать на сходимость интеграл .

Решение. Очевидна оценка подынтегральной функции: . Интеграл

.

Следовательно, интеграл сходится абсолютно, причем

. ◄