1. ФУНКЦИИ НЕСКОЛЬКИХ ВЕЩЕСТВЕННЫХ ПЕРЕМЕННЫХ. ОСНОВНЫЕ ПОНЯТИЯ
1.1.
Говорят, что задана функция
двух независимых переменных
,
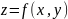если задан закон,
т. е. правило соответствия
между парами чисел
и числами
.
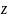При этом независимые переменные
и
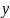называются аргументами,
а зависимая переменная
– значением
этой
функции
.
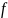Каждой паре аргументов
и
соответствует
определенная точка
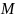на координатной плоскости с координатами
,
и вместо того, чтобы говорить о значении
функции при значениях аргументов
и
,
можно
говорить о значении функции
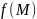в точке
.
Функция может быть определена на всей
плоскости или только в какой-то ее части,
в некоторой области
,
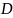которая называется областью
определения функции.
Множество
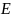возможных значений чисел
для функции
называется областью
ее значений.
Если
функция
задана аналитически,
то есть переменные
,
и
связаны некоторым уравнением, то область
определения функции
получается из возможности выполнить
указанные действия. В частности, если
функция
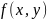есть многочлен от
и
,
например,
,
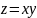то можно считать, что эта функция
определена на всей плоскости. Формула
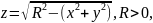задает функцию при условии:
.
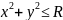Это условие означает, что область
определения функции
- круг с центром в начале координат и
радиусом, равным
.
Графически
функция двух переменных может быть
изображена в виде поверхности в трехмерном
пространстве с декартовой системой
координат
.
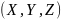В частности, график функции
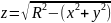– полусфера, расположенная над областью
определения
,
а график
функции
– гиперболическая поверхность, имеющая
седловую точку с координатами (0, 0).
Окрестностью
точки
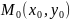(обозначение:
)
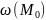называется множество точек
,
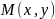удовлетворяющих строгому неравенству:
,
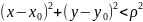т.е. внутренность круга с центром в точке
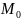любого радиуса
.
Если требуется указать радиус круга,
например,
,
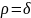то такая окрестность называется
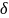-окрестностью
и
обозначается
.
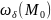Точка
называется внутренней
точкой множества
,
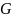если существует окрестность
целиком принадлежащая этому множеству
(
).
Точка
называется граничной
точкой множества
,
если любая окрестность
содержит точки, как принадлежащие
множеству
,
так и не принадлежащие множеству
.
Все множество граничных точек образует
границу
множества
.
Если множество содержит свою границу,
то оно называется замкнутым,
если множество не содержит границу, то
оно называется открытым.
Примером
замкнутого множества является область,
описываемая неравенствами:
,
.
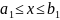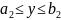Это
- прямоугольник со сторонами, параллельными
осям координат, причем граница этого
прямоугольника, состоящая из отрезков,
лежащих на прямых:
,
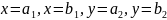также включается в область. Неравенства
,
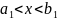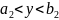определяют только внутренние
точки
прямоугольника и, следовательно, -
открытую область. Любая окрестность
также является открытым множеством.
Аналогично
определяются функция
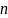независимых
переменных
,
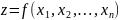ее область определения и область
значений.
Все множество последовательностей вида
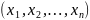называется
–мерным
пространством
и обозначается
,
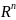сами последовательности
– точками
пространства
,
а числа
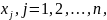– координатами
этой точки.
Аналогично
окрестностью
точки
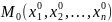называется множество точек
,
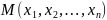удовлетворяющих
неравенству:
,
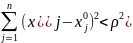вводятся понятия внутренней
и граничной
точки,
замкнутого
и
открытого
множества
в пространстве
.
В основном дальше рассматриваются функции двух переменных, сформулированные утверждения нетрудно перенести на функции переменных.
1.2. Введем понятие предела для функции двух переменных.
Пусть
функция
определена во всех точках
,
достаточно близких к точке
,
за исключением, может быть, ее самой.
Число
называется пределом
функции
при
стремлении точки
к точке
,
обозначение:
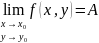или
,
если
для любого заданного положительного
числа
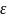существует такое положительное число
,
что выполняется неравенство
.
(1.1)
Заметим,
что неравенства
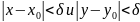в (1.1) могут быть заменены на условие:
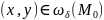(точки
принадлежат
-окрестности точки
).
Обращаем
внимание, что
и
стремятся к своим предельным значениям
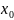и
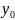независимо друг от друга.
При
этом предполагается, что исключена пара
значени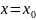й
и
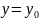(точка
не совпадает с
).
Если точка
лежит на границе той области, в которой
определена
,
то
,
стремящаяся к
,
должна принадлежать области, в которой
определена функция
.
Пусть
имеется какая-либо пронумерованная
последовательность точек
,
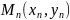стремящаяся к
,
т. е. такая, что последовательность
имеет предел
,
а последовательность
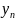имеет предел
.
Доказано, что если последовательность
чисел
для любой такой последовательности
точек
имеет один и тот же предел
,
то число
есть предел функции
при стремлении
к
в смысле сформулированного выше
определения.
Так как определение (1.1) практически совпадает с определением предела функции одного вещественного переменного, теоремы о пределах сохраняются для функций двух переменных.
Кроме предельного перехода (1.1), можно рассматривать повторные пределы, соответствующие предельному переходу сначала по при постоянном , отличном от , а затем по , или наоборот:
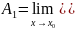или
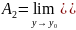(1.2)
Из
существования предела в смысле двух
переменных (1.1) следует существование
и совпадение повторных пределов:
.
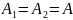Обратное – неверно.
1.3. Пусть функция определена в точке и во всех точках , достаточно близких к . Функция называется непрерывной в точке , если
,
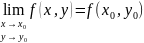или
.
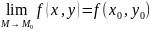(1.3)
Определение (1.3) также совпадает с определением непрерывности функции одного вещественного переменного, поэтому теоремы о свойствах непрерывных функций сохраняются для функций двух переменных.
Приведем
очевидное следствие,
которое вытекает из определения
непрерывности функции. Если функция
двух переменных
непрерывна в точке
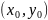и, если мы положим
,
то функция
одной переменной
непрерывна в точке
.
Аналогично,
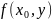непрерывна в точке
.
Функция называется непрерывной в некоторой открытой области, если она непрерывна в каждой точке этой области (внутренней точке).
Функция
называется непрерывной
в замкнутой области,
если она непрерывна в каждой внутренней
точке
этой области, а в граничных
точках
соотношение (1.3) выполняется при любом
стремлении точек
изнутри области.
Пусть - ограниченная замкнутая область на плоскости и непрерывная в функция. Такая функция обладает свойствами, аналогичными свойствам функции одной независимой переменной, непрерывной в конечном замкнутом промежутке. Доказательства этих свойств, по существу, те же, что и доказательства для функции одной независимой переменной. Сформулируем лишь результаты.
1.
Функция
ограничена в
,
т. е. существует такое положительное
число
,
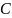что
для всех
.
2. Функция достигает в наибольшего и наименьшего значений (теорема Вейерштрасса).
1.4.
Допустим, что у функции
переменная
сохраняет постоянное значение
и меняется только
,
то есть функция
становится функцией одного переменного
и можно вычислить ее приращение и
производную в точке
.
Обозначим это приращение
функции
через
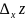(такое приращение называется частным
приращением):
.
Частной
производной первого порядка
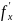или
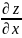функции
по переменной
в
точке
называется предел
,
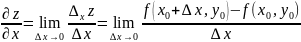(1.4)
если он существует и конечен.
Если имеет частную производную по , то она, как известно, является непрерывной функцией аргумента при фиксированном .
Точно так же определяется частное приращение
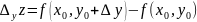
и
частная
производная первого порядка
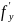или
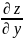функции
по переменной
в точке
,
вычисленная в предположении, что
не меняется.
То есть
.
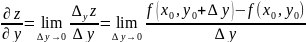(1.5)
Так как определения (1.4) и (1.5) совпадают с определением производной функции одной переменной, то при вычислении частных производных используются обычные правила и приемы дифференцирования.
Аналогично через частные приращения определяются частные производные функции независимых переменных .