ИСиТ / 09.03.02 Интеллектуальные информационные системы и технологии / 2 курс 2 семестр / Алексеев Александр Борисович / Высшая математика / Высшая математика / 2семестр / MA2dvoinoiintegralvdekartovih

2. ДВОЙНОЙ ИНТЕГРАЛ

2.1. Пусть в ограниченной плоской области определена функция точки . Разобьем область на подобластей (см. рис. 3). Обозначим через площадь подобласти , через – ее диаметр (наибольшее расстояние между двумя любыми точками ). Введем ранг разбиения . В каждой подобласти выберем точку и составим интегральную сумму

. (2.1)

Двойным интегралом от функции по области называется предел интегральной суммы при

, (2.2)

если этот предел существует и конечен независимо от разбиения области и выбора точек . Функция точки в этом случае называется интегрируемой в области .

Рис. 3.

Так как алгоритм определения двойного интеграла повторяет соответствующий алгоритм для определенного интеграла, то свойства двойного интеграла аналогичны свойствам определенного интеграла. А именно, имеют место свойства линейности, аддитивности и т.п. В частности, если , то равен площади области , то есть

. (2.3)

Можно доказать, что, если функция непрерывна в области , то она в ней интегрируема. Верны также теорема о «среднем», теорема об интегрировании неравенств и т.д.

2.2. Пусть функция непрерывна в области и принимает положительные значения. Доказано, что равен объёму тела, ограниченного сверху графиком функции , с боков – цилиндрической поверхностью, вырезающей на плоскости область , и снизу – плоскостью (рис. 4), то есть

. (2.4)

Рис. 4.

2.3. Введем на плоскости декартову систему координат. Пусть в области задана интегрируемая функция , которую теперь можно рассматривать как функцию двух переменных , где – декартовы координаты точки . Так как интеграл – это предел интегральной суммы, независящий от способа разбиения области , разобьем область на подобласти (здесь удобнее подобласти нумеровать двумя индексами, а не одним) линиями, параллельными осям координат. В этом случае большинство подобластей разбиения (кроме приграничных) будут прямоугольниками площади, равной произведению , где – длина стороны участка разбиения, параллельной оси , а – длина стороны участка разбиения, параллельной оси . Двойной интеграл, полученный в результате такого разбиения, называется двойным интегралом в декартовых координатах и обозначается символом

. (2.5)

Пусть область – прямоугольник со сторонами, параллельными осям координат: , . Тогда подобное разбиение будет содержать только прямоугольники площади , где – длина участка разбиения интервала на оси , а – длина участка разбиения интервала на оси , и можно доказать, что вычисление двойного интеграла в декартовых координатах сводится к вычислению двух определенных интегралов. Верны следующие формулы:

, (2.6)

. (2.7)

Если область – выпукла (см. рис. 5), то формулы (2.6) и (2.7) принимают вид:

, (2.8)

. (2.9)

Рис. 5.

Здесь 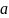и ( и ) – пределы, в которых зажата область по оси (по оси ), ( 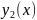) – функция, графиком которой является нижняя (верхняя) часть границы, а ( ) – функция, графиком которой является левая (правая) часть границы.

Интегралы в правой части формул (2.6) - (2.9) дают способ вычисления двойного интеграла в декартовых координатах и называются повторными. Доказательства формул (2.8) и (2.9) получаются из (2.6) и (2.7), соответственно, если поместить область в прямоугольник (см. рис. 5), продолжить на него функцию нулем и применить свойство аддитивности.

Для вычисления двойного интеграла по любой области следует разбить ее на удобные для формулы (2.7) (или (2.8)) подобласти и применить свойство аддитивности.

Пример 2.1. Найти объем пирамиды (см. рис. 6), ограниченной плоскостями: .

Рис. 6.

Решение. Область в двойном интеграле (2.3) для нашей пирамиды – треугольник с границами: , функция: . Тогда формула (2.7) принимает вид:

. ◄

2.4. Кроме вычисления объема (2.4) и площади (2.3) двойной интеграл можно применять для вычисления площади поверхности.

Пусть поверхность является графиком однозначной функции , определенной в области , причем частные производные

,

– непрерывные функции в этой области. В этом случае поверхность является гладкой, и ее площадь вычисляется с помощью интеграла вида (2.5), где роль подынтегральной функции играет . То есть площадь такой поверхности

. (2.10)