6. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
6.1. Обыкновенным дифференциальным уравнением называется уравнение, в которое, кроме независимой переменной и неизвестной функции, входят производные этой функции или ее дифференциалы.
Общий вид обыкновенного дифференциального уравнения:
,
(6.1)
где
– независимая переменная и
– искомая функция этой переменной.
Число
-
наивысший
порядок производных
неизвестной функции, входящих в уравнение,
называется порядком
дифференциального уравнения.
В частности, обыкновенным дифференциальным уравнением первого порядка называется уравнение вида
.
(6.2)
Решением
(частным решением) дифференциального
уравнения
называется любая функция
,
которая при подстановке в уравнение
обращает его в тождество.
Частные случаи уравнений (6.1) и (6.2):
,
(6.3)
(6.4)
называются дифференциальными уравнениями, разрешенными относительно старшей производной.
В простейшем случае, уравнение (6.4) имеет вид
.
(6.5)
Нахождение его решений есть основная задача интегрального исчисления, и все множество этих решений дается формулой
,
(6.6)
где
–
какая-то первообразная функции
,
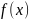– произвольная постоянная. Таким
образом, уравнение (6.5) имеет семейство
решений, зависящее от произвольной
постоянной, при этом любое частное
решение получается из формулы (6.6) при
конкретных значениях постоянной
.
Аналогично,
уравнение (6.2) (или (6.4)) имеет семейство
решений
,
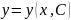зависящее
от произвольной постоянной, из которого
получаются частные решения при конкретных
значениях постоянной
.
Такое решение называется общим
решением
уравнения (6.2) (или (6.4)).
Общим
решением
уравнения (6.1) (или (6.3)) является семейство
решений
,
зависящее
от произвольных постоянных
,
из которого получаются частные решения
при конкретных значениях постоянных
.
Задача, в которой требуется найти решение дифференциального уравнения (6.4), удовлетворяющее начальному условию
,
(6.7)
где
,
–
заданные числа, называется задачей
Коши.
Доказана Теорема существования и единственности решения задачи Коши для уравнения 1-го порядка (6.4).
Пусть
функция
непрерывна и имеет непрерывную частную
производную
в окрестности точки с координатами (
,
).
Тогда задача Коши для уравнения (6.4)
с условием (6.7)
имеет
в этой окрестности единственное решение.
Если известно общее решение уравнения (6.4), то, используя условие (6.7), получим уравнение
для отыскания значения постоянной , соответствующего решению заданной задачи Коши.
Уравнение
(6.4)
может иметь решения, которые не получаются
из общего решения
ни при каком значении постоянной
.
Такие решения называются особыми
решениями.
Они
могут существовать только в окрестности
тех точек
,
где не выполнены условия теоремы
существования и единственности решения
задачи Коши. То же самое верно и для
уравнения
- го
порядка
(6.3).
(Подробнее (см.[.]).
Здесь мы особые решения рассматривать
не будем.)
Задача Коши для уравнения - го порядка (6.3) формулируется с помощью условий:
,
,
(6.8)
где
,
–
заданные числа. Для этой задачи Коши
также доказана теорема
существования и единственности.
Пусть
функция
переменных
непрерывна и имеет непрерывные частные
производные
в окрестности точки с координатами (
,
).
Тогда задача Коши для уравнения (6.3)
с условиями (6.8)
имеет
в этой окрестности единственное решение.
Если известно общее решение уравнения (6.3), зависящее от произвольных постоянных, то значения этих постоянных, соответствующие решению заданной задачи Коши, находятся из системы (6.8) уравнений с неизвестными.
6.2. Дифференциальным уравнением 1-го порядка с разделенными переменными называется уравнение вида
,
(6.9)
где
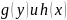– непрерывные функции. Из равенства
дифференциалов (6.9)
следует равенство неопределенных
интегралов
,
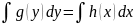(6.10)
которое равносильно равенству
.
(6.11)
Здесь
–
первообразные функций
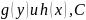- произвольная постоянная. Равенство
(6.11) описывает
(в неявной форме) общее решение уравнения
(6.9).
Уравнение
1-го порядка, которое с помощью
арифметических действий и выражения
производной через дифференциалы
можно представить в виде (6.9) называется
дифференциальным
уравнением
с
разделяющимися переменными.
Пример
6.1.
Решить уравнение:
.
Решение.
Приведем уравнение к виду (6.9). Получим
.
Тогда
,
и,
следовательно,
(здесь
произвольную постоянную удобнее
обозначить через
).
Окончательно получаем общее
решение в виде (модуль можно убрать в
силу произвольности постоянной
):
.
6.3. Однородным дифференциальным уравнением 1-го порядка называется уравнение (6.4), если функция обладает свойством однородности, то есть
1
(6.12)
для
любого допустимого числа
.
В этом случае
.
Введем
вместо
новую искомую функцию
,
откуда
и
.
Поставляя в уравнение (6.4), получим
уравнение с разделяющимися переменными
.
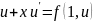Следовательно,
если
,
то
.
Тогда общее решение уравнения (6.4) можно написать в виде
,
где
– первообразная функции
,
– произвольная постоянная.
Заметим,
что случай равенства
разобран в примере
6.1.
Пример
6.2.
Решить уравнение:
.
Решение. Перепишем уравнение для переменной , тогда
.
После преобразований и разделения переменных получим
Следовательно,
.
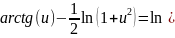Окончательно, общее решение в неявном
виде:
.
6.4. Линейным дифференциальным уравнением 1-го порядка называется уравнение вида
,
(6.13)
где
и
– заданные
непрерывные функции. При
этом, если функция
,
то
уравнение называется
однородным,
в противном случае – неоднородным.
Однородное уравнение
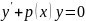(6.14)
является уравнением с разделяющимися переменными и легко решается по схеме п. 6.2.
Неоднородное уравнение (6.13) может быть решено, например, методом Бернулли. А именно, ищем решение в виде произведения двух неизвестных функций
.
(6.15)
Подставляя
(см. (6.15)) и производную
в уравнение (6.13), получим
.
(6.16)
Выбирая
вспомогательную функцию (частное
решение)
так, чтобы она удовлетворяла однородному
уравнению
,
для функции
из уравнения (5.16)
получим уравнение
,
(6.17)
которое
является уравнением вида (6.5). Для него
находим общее решение и, подставив
найденные функции
в (6.15), получим общее решение уравнения
(6.13).
Пример
6.3.
Решить уравнение:
.
Решение. В нашем случае уравнение (6.16) принимает вид
.
Выбираем вспомогательную функцию так, чтобы она удовлетворяла однородному уравнению
.
Переменные делятся, тогда
.
Частное
решение
подставляем в уравнение (6.17),
получим
.
Тогда
,
где
–
произвольная постоянная, следовательно,
– общее решение исходного уравнения.