
ИСиТ / 09.03.02 Интеллектуальные информационные системы и технологии / 2 курс 2 семестр / Алексеев Александр Борисович / Высшая математика / Высшая математика / 2семестр / Krivolineinieintegrali
.docx
4. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4.1. Определение криволинейного интеграла первого рода подобно определениям определенного, двойного и тройного интегралов, только областью интегрирования здесь является кривая линия.
А
именно, пусть в трехмерном пространстве
задана некоторая кривая
 .
Пусть точка
.
Пусть точка
 -
начало и точка
-
начало и точка
 –
конец
этой кривой. Положим, что на
задана непрерывная функция точки
–
конец
этой кривой. Положим, что на
задана непрерывная функция точки
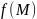 .
Разделим кривую
на
.
Разделим кривую
на
 частей точками:
частей точками:
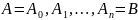 (см.рис.16).
(см.рис.16).
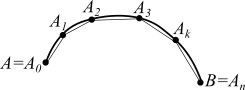
Рис.16.
На
каждом участке разбиения
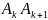
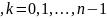 ,
возьмем какую-нибудь точку
,
возьмем какую-нибудь точку
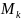 и
составим интегральную сумму
и
составим интегральную сумму

где
 длина дуги
кривой
.
Введем ранг разбиения
длина дуги
кривой
.
Введем ранг разбиения
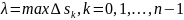 .
Предел интегральной суммы при
.
Предел интегральной суммы при
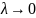 ,
не зависящий ни от способа разбиения,
ни от выбора точек
,
называется криволинейным
интегралом первого рода
(другое название: «по длине») от функции
по
и обозначается так:
,
не зависящий ни от способа разбиения,
ни от выбора точек
,
называется криволинейным
интегралом первого рода
(другое название: «по длине») от функции
по
и обозначается так:
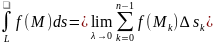 .
(4.1)
.
(4.1)
Положение
переменной точки
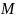 кривой
определяется длиною дуги, сосчитанной
от точки
:
кривой
определяется длиною дуги, сосчитанной
от точки
:
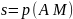 ,
так что функцию
можно
считать функцией независимой переменной
,
так что функцию
можно
считать функцией независимой переменной
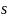 ,
т. е.
,
т. е.
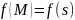 ,
и интеграл
(4.1)
вычисляется
с помощью обычного определенного
интеграла
,
и интеграл
(4.1)
вычисляется
с помощью обычного определенного
интеграла
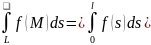 ,
(4.2)
,
(4.2)
где
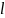 –
длина дуги кривой
.
Заметим, что кривая
может быть и замкнутой, т. е. точка
может совпадать с точкой
.
–
длина дуги кривой
.
Заметим, что кривая
может быть и замкнутой, т. е. точка
может совпадать с точкой
.
Так
как определение криволинейного интеграла
первого рода (4.1) и формула вычисления
(4.2) аналогичны соответствующим формулам
для определенного интеграла, свойства
криволинейного интеграла первого рода
аналогичны свойствам определенного
интеграла. В частности, если подынтегральная
функция
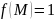 ,
то криволинейный интеграл (4.2)
вычисляет длину всей кривой
:
,
то криволинейный интеграл (4.2)
вычисляет длину всей кривой
:
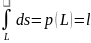 .
(4.3)
.
(4.3)
4.2.
Введем
в трехмерном пространстве декартову
систему координат. Положение точки
определяется координатами
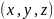 и
функцию точки
теперь
можно рассматривать как функцию трех
переменных
и
функцию точки
теперь
можно рассматривать как функцию трех
переменных
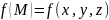 .
Пусть кривая
задана параметрически,
то есть координаты точки на кривой
вычисляются как значения функций,
зависящих
от дополнительной переменной (параметра)
.
Пусть кривая
задана параметрически,
то есть координаты точки на кривой
вычисляются как значения функций,
зависящих
от дополнительной переменной (параметра)
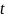 ,
,

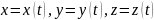 ,
где
,
где
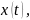
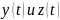 имеют непрерывные производные для
имеют непрерывные производные для
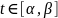 ,
причем точка
соответствует значению
,
причем точка
соответствует значению
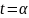 ,
а точка
- значению
,
а точка
- значению
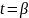 .
Тогда интеграл
(4.1)
вычисляется
по формуле
.
Тогда интеграл
(4.1)
вычисляется
по формуле
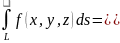
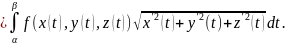 (4.4)
(4.4)
Если
кривая лежит в плоскости
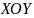 ,
то
,
то
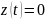 и формула (4.4) принимает вид
и формула (4.4) принимает вид
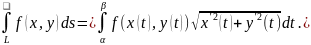 (4.5)
(4.5)
Если
дуга
является графиком однозначной функции
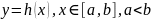 ,
то за параметр
можно взять переменную
,
то за параметр
можно взять переменную
 .
Тогда
.
Тогда
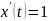 ,
и формула (4.5) принимает вид
,
и формула (4.5) принимает вид
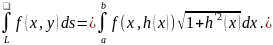 (4.6)
(4.6)
Аналогично
строится формула,
если дуга
является графиком однозначной функции
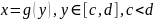 .
.
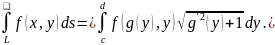 (4.7)
(4.7)
Пример
4.1. Вычислить
криволинейный интеграл
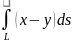 ,
где
– окружность, задаваемая уравнением
,
где
– окружность, задаваемая уравнением
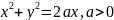 .
.
Решение.
Уравнение
заданной окружности преобразуется к
виду
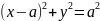 ,
для которого
удобно
параметрическое описание:
,
для которого
удобно
параметрическое описание:
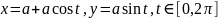 .
.
Тогда
 ,
и
,
и
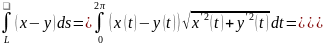
 .
◄
.
◄
4.3.
Пусть в трехмерном пространстве введена
декартова система координат. Зададим
на кривой
направление, кривая
с направлением называется путем.
Пусть точка
-
начало и точка
-
конец
этого пути. Пусть на кривой
заданы три непрерывные функции:
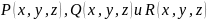 .
Разделим, как и в п.1
(см.рис.16),
кривую
на
частей точками:
.
На
каждом участке разбиения
,
возьмем какую-нибудь точку
с координатами
.
Разделим, как и в п.1
(см.рис.16),
кривую
на
частей точками:
.
На
каждом участке разбиения
,
возьмем какую-нибудь точку
с координатами
 .
Обозначим через
.
Обозначим через
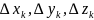 проекции вектора (направленного в
соответствии с направлением на кривой
)
проекции вектора (направленного в
соответствии с направлением на кривой
)
 на оси
на оси
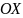 ,
,
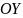 и
и
 .
Очевидно, что при
одновременно и
.
Очевидно, что при
одновременно и
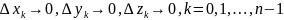 .
Составим интегральную сумму вида:
.
Составим интегральную сумму вида:
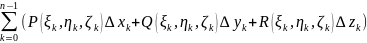 .
(4.8)
.
(4.8)
Предел этой суммы при , не зависящий ни от способа разбиения, ни от выбора точек называется криволинейным интегралом второго рода (другое название: «по координатам») и обозначается так:
 .
(4.9)
.
(4.9)
Связь между интегралами (4.9) и (4.1) устанавливается формулой:

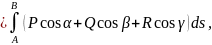 (4.10)
(4.10)
где
 направляющие косинусы вектора
направляющие косинусы вектора
 –
единичного (
–
единичного (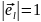 )
вектора касательной в каждой точке к
кривой
,
направление которого совпадает с
направлением, заданным на кривой. И эти
направляющие косинусы, и функции
)
вектора касательной в каждой точке к
кривой
,
направление которого совпадает с
направлением, заданным на кривой. И эти
направляющие косинусы, и функции
 можно считать функциями аргумента
вдоль кривой
.
можно считать функциями аргумента
вдоль кривой
.
Следовательно, свойства интеграла (4.9) аналогичны свойствам интеграла (4.1), причем можно заметить, что в силу (4.10) интеграл (4.9) меняет знак при смене направления на кривой .
Если функции рассматривать как координаты некоторой вектор-функции в трехмерном пространстве:
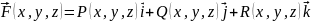 ,
,
где
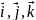 – орты координатных осей
– орты координатных осей
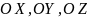 соответственно,
то подынтегральное выражение в интеграле
(4.10) представляет собой скалярное
произведение этой вектор-функции
соответственно,
то подынтегральное выражение в интеграле
(4.10) представляет собой скалярное
произведение этой вектор-функции
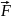 и вектора
.
и вектора
.
Способ вычисления криволинейного интеграла второго рода также связан с параметрическим заданием кривой. А именно, пусть координаты точки на кривой вычисляются как значения функций, зависящих от параметра , , где имеют непрерывные производные для , причем точка соответствует значению , а точка - значению . Тогда интеграл (4.9) вычисляется по формуле
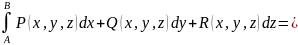
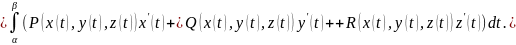 (4.11)
(4.11)
Если кривая лежит в плоскости , то вычисление криволинейного интеграла второго рода упрощается. В этом случае в параметрическом задании кривой , и формула (4.11) принимает вид

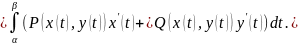 (4.12)
(4.12)
В частности, если кривая является графиком однозначной функции , и направление на ней совпадает с направлением оси , то за параметр можно взять переменную . Тогда , и формула (4.12) принимает вид
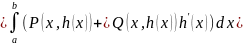 .
(4.13)
.
(4.13)
Аналогична формула и в случае, когда кривая является графиком однозначной функции , и направление на ней совпадает с направлением оси :
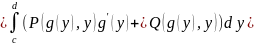 .
(4.14)
.
(4.14)
Пример 4.2. Вычислить криволинейный интеграл
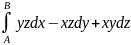
по кривой, которая является витком винтовой линии:
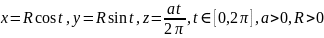 .
.
Решение.
Производные:
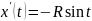 ,
,
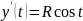 ,
,
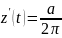 .
Тогда по формуле (4.11)
.
Тогда по формуле (4.11)
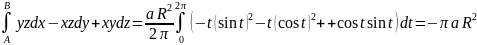 .
◄
.
◄
4.4.
Формула
Грина устанавливает связь между двойным
интегралом по плоской области
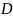 и интегралом по ее границе
.
и интегралом по ее границе
.
Пусть
область
выпуклая, т.е. граница области
любой прямой пересекается только в двух
точках. Пусть в области
заданы две непрерывные функции
 ,
имеющие непрерывные производные. Тогда
верна формула
,
имеющие непрерывные производные. Тогда
верна формула
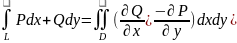 ,
(4.15)
,
(4.15)
которая носит имя Грина, причем кривую нужно обходить против часовой стрелки.
Области более общего вида надо разбить на удобные подобласти, к каждой применить формулу (4.15), а затем - свойство аддитивности для интегралов.
Подобные рассуждения применимы и к тому случаю, когда область ограничена несколькими кривыми (область с «дырками» называется многосвязной областью). При этом в левой части (4.15) надо интегрировать по всем граничным кривым, причем по внешнему контуру надо интегрировать против часовой стрелки, а по внутренним контурам по часовой стрелке, т. е. по всем контурам так, чтобы область оставалась слева.
4.5.
Из
формулы (4.15) следует, что, если функции
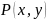 и
и
 таковы,
что
таковы,
что
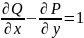 ,
(4.16)
,
(4.16)
то
криволинейный интеграл в (4.15) численно
равен площади области
.
Например, можно взять
 ,
,
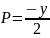 .
Тогда
.
Тогда
 (4.17)
(4.17)
Пример 4.3. С помощью криволинейного интеграла найти площадь фигуры, ограниченной эллипсом. (Сравните с вычислением по формуле (2.16)).
Решение. Используем параметрическое описание эллипса:
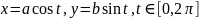 .
.
Тогда
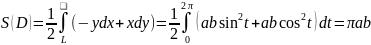 .
◄
.
◄
4.6. В некоторых случаях величина криволинейного интеграла
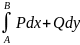 (4.18)
(4.18)
не зависит от пути интегрирования, но лишь от начальной и конечной точек интегрирования, а в других случаях вид самого пути влияет на величину интеграла. Из формулы Грина получаются условия, при которых интеграл (4.18) не зависит от пути интегрирования.
Пусть в односвязной (без «дырок») области заданы непрерывные функции и , имеющие непрерывные производные. Легко доказать, что интеграл (4.18) не зависит от пути интегрирования в области , если
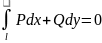 (4.19)
(4.19)
для любого замкнутого контура , лежащего в области . Из формулы Грина следует, что необходимым и достаточным условием для выполнения равенства (4.19) является условие
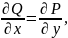 (4.20)
(4.20)
которое должно выполняться в любой точке области .
Пусть
в односвязной области
выполнено условие (4.20). Рассмотрим
интеграл (4.18), в котором закреплена точка
 ,
а точку
,
а точку
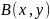 будем считать переменной. Тогда интеграл
(4.18) будет функцией переменных
будем считать переменной. Тогда интеграл
(4.18) будет функцией переменных
 или, как говорят, функцией точки
с координатами
:
или, как говорят, функцией точки
с координатами
:
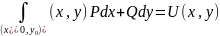 .
(4.21)
.
(4.21)
Верны следующие свойства этой функции.
1.
У
функции
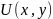 существуют
частные производные,
причем
существуют
частные производные,
причем
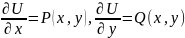 .
(4.22)
.
(4.22)
2. Из (4.22) следует, что подынтегральное выражение в (4.21) является полным дифференциалом функции :
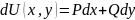 .
.
3.
Если
выражение
 является
полным дифференциалом некоторой функции
является
полным дифференциалом некоторой функции
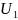 ,
то
,
то
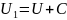 ,
где
,
где
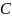 –
некоторая постоянная.
–
некоторая постоянная.
То
есть условие (4.20) является необходимым
и достаточным для того, чтобы выражение
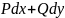 было
полным дифференциалом некоторой функции.
было
полным дифференциалом некоторой функции.
Заметим,
что интеграл (4.21) можно
вычислять по любому пути, соединяющему
точки
и
.
Оказывается, что самый простой путь
интегрирования – ломаная, состоящая
из двух отрезков, параллельных осям
координат. Тогда, если первый отрезок
параллелен оси
,
т.е. переменная
 не
меняется, а второй – оси
(не меняется переменная
),
то мы получаем следующий способ
вычисления
интеграла (4.21):
не
меняется, а второй – оси
(не меняется переменная
),
то мы получаем следующий способ
вычисления
интеграла (4.21):
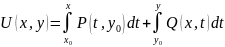 .
(4.23)
.
(4.23)
Пример 4.4. Вычислить криволинейный интеграл
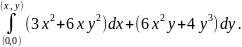
Решение. Проверим условие (4.20):
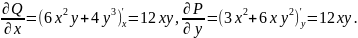
То
есть
и интеграл не зависит от пути интегрирования.
Будем вычислять его по ломаной, состоящей
из двух отрезков, параллельных осям
координат, где первый отрезок (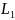 )
параллелен оси
,
а второй (
)
параллелен оси
,
а второй (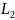 )
– оси
:
)
– оси
:
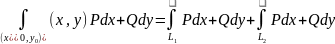 .
.
Здесь
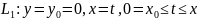 ,
,
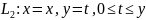 .
.
Тогда (см. формулу (4.23))
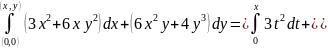
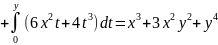 .
◄
.
◄
