МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Математические основы защиты информации

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №3

Обычный и бинарный алгоритмы Евклида

10.03.01 Информационная безопасность

ФИО:

Группа:

Преподаватель: Кушнир Д.В.

Санкт-Петербург

Содержание

Алгоритм Евклида 3

Бинарный алгоритм Евклида 4

Теоретическая часть по исследуемому вопросу

Нахождение наибольшего общего делителя числе a и b: НОД(a,b). Один из путей решения – разложить каждое из чисел на множители и найти в двух разложениях максимальный совпадающий, однако такой подход является неэффективным (имеет экспоненциальную сложность).

Алгоритм Евклида

Алгоритм в общем виде: Найти: НОД(a,b) a =b *q₁ + r₁ 0≤ri<b //q1-целое,r1-остаток от деления a на b * b =r₁ *q₂ + r₂ 0≤r2<r1

r_n-3=r_n-2 *q_n-1 +r_n-1 r_n-2=r_n-1 *q_n +0 rn=0

Ответ: НОД(a,b)=rn-1 //ответ – последний ненулевой остаток.

Пример НОД(1234,54) 1234 = 54*22+46 54=46*1+8 46=8*5+6 8=6*1+2 6=2*3+0 Последний ненулевой остаток 2, т.е. НОД(1234,54)=2

Формализованное описание алгоритма Эвклида: Алгоритм НОД(a,b) a>b Начальные присвоения A=a; R=B=b;

В цикле выполняем: a) R=остаток от деления A на B; IF(R=0) B – ответ b) A=B; c) B=R;

Пример НОД(24;15)

A B q R 24 15 24 = 15 * 1 + 9 15 = 9 * 1 + 6 9 = 6 * 1 + 3 6 = 3 * 2 + 0

Бинарный алгоритм Евклида

Бинарный алгоритм Евклида вычисления НОД оказывается более быстрым при реализации этого алгоритма на компьютере, поскольку использует двоичное представление чисел а и b.

Бинарный алгоритм Евклида основан на следующих свойствах наибольшего общего делителя (считаем, что 0 < b ≤ а): 1) если оба числа а и b четные, то НОД(a,b) = 2 · НОД(a/2 , b/2) 2) если число а нечетное, число b четное, то НОД(a, b) = НОД(а, b/2); 3) если оба числа а и b нечетные, а > b, то НОД(а, b) = НОД(а – b, b); 4) если а = b, то НОД(а, b) = а.

Формализованное описание алгоритма Бинарного алгоритма Евклида. Вход: Целые числа a, b; 0 < b ≤ а. Выход. d = HOД(a,b). 1. Положить g ← 1. 2. Пока оба числа а и b четные, выполнять а← a/2 , b ← b/2, g ← 2g до получения хотя бы одного нечетного значения а или b. 3. Положить u ← a, v ← b. 4. Пока u ≠ 0, выполнять следующие действия. 4.1. Пока u четное, полагать u ← u/2. 4.2. Пока v четное, полагать v ← v/2. 4.3. При u ≥ v положить: u ← u–v, в противном случае: v ← v–u. 5. Положить d ← gv. 6. Результат: d. Р

Задание

1. Выполнить «вручную» вычисление НОД(a,b) алгоритмом Евклида.

2. Выполнить вычисление НОД(a,b) алгоритмом Евклида в среде Excel (в ячейках таблицы) или в любой другой программной среде, которая позволяет выводить промежуточные шаги выполнения алгоритма.

3. Выполнить «вручную» вычисление НОД(a,b) бинарным алгоритмом Евклида.

4. Выполнить вычисление НОД(a,b) бинарным алгоритмом Евклида в среде Excel или в любой другой программной среде, которая позволяет выводить промежуточные шаги выполнения алгоритма.

Вариант 22. НОД(a,b) для ручного выполнения: a=20 b=24 НОД(a,b) для программного выполнения: a= 3198268 b= 4859598

Ход работы

1. НОД(24,20) «вручную» алгоритмом Евклида

24 = 20*1+4 20 = 4*5+0 Последний остаток перед делением нацело = 4, значит НОД(24,20) = 4 ИЛИ представляем числа в таком виде и ищем общие множители. 24 = 2*2*2*3 20 = 2*2*5 Так как у нас есть общие множители, то они перемножаются 2*2=4, значит НОД(24,20)=4

2. НОД(4859598, 3198268) в языке программирования Python алгоритмом Евклида.

Код программы:

# Алгоритм Евклида и бинарный алгоритм Евклида

def evklid_algoritm(a, b):

while a != 0 and b != 0:

if a >= b:

a %= b

else:

b %= a

return a or b

def evlkid_bin_algoritm(a, b):

k = 1

if a == b:

return (a)

# Пока а и б не равны нулю выполняется цикл

while (a != 0) and (b != 0):

# Если а и б четные

while (a % 2 == 0) and (b % 2 == 0):

a /= 2

b /= 2

k *= 2

# Если а четное то a/2, если б четное то b/2

while a % 2 == 0:

a /= 2

while b % 2 == 0:

b /= 2

# Если оба числа нечетные, то а-б или б-а

if a >= b:

a -= b

else:

b -= a

return b * k

print("Введите номер необходимого алгоритма")

print("1 - Алгоритм Евклида (НОД)")

print("2 - Бинарный алгоритм Евклида (НОД)")

vibor = int(input())

if vibor == 1:

print("\nВыбран обычный алгоритм")

a = int(input("Введите число a:"))

b = int(input("Введите число b:"))

print(evklid_algoritm(a, b))

elif vibor == 2:

print("\nВыбран бинарный алгоритм")

a = int(input("Введите число a:"))

b = int(input("Введите число b:"))

c = evlkid_bin_algoritm(a, b)

if c != 'Error':

print(c)

else:

print("\nВведен некорректный номер алгоритма")

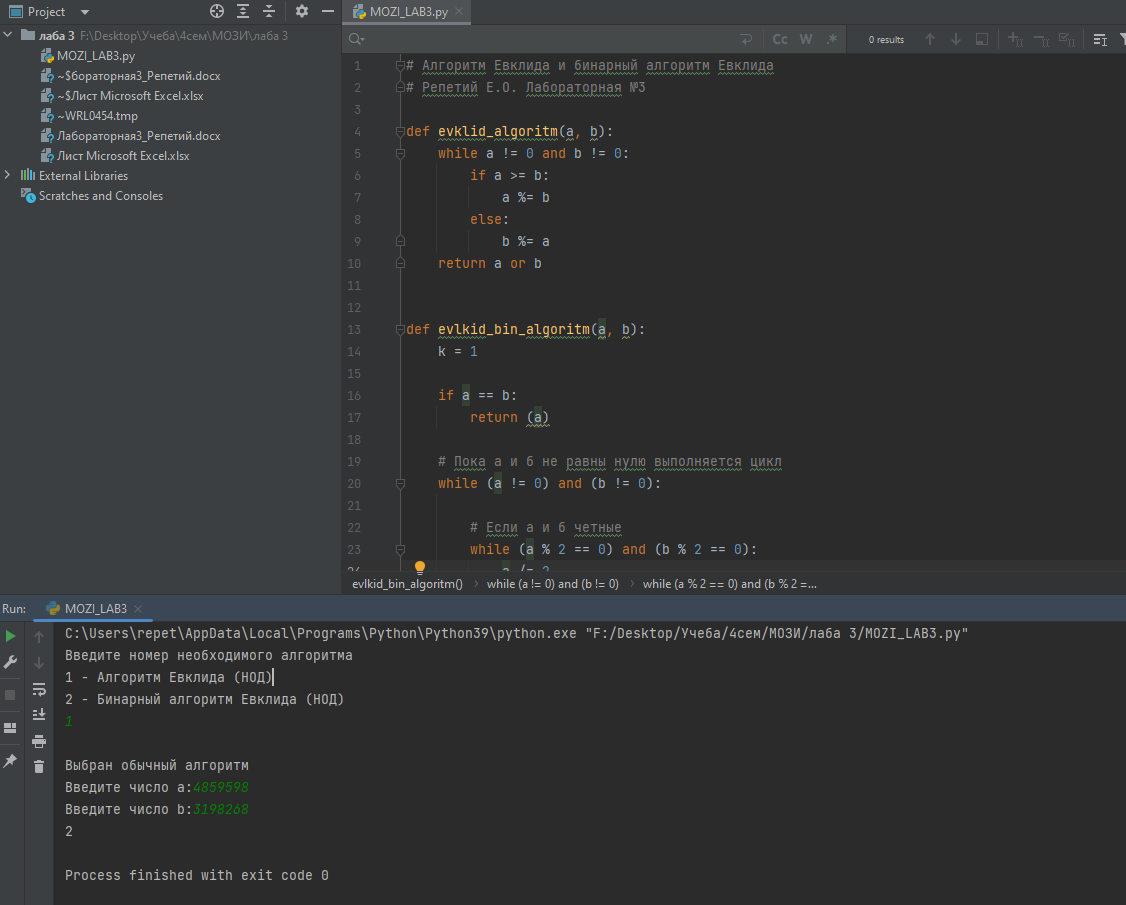
Результат работы программы:

3. НОД(24,20) «вручную» бинарным алгоритмом Евклида

НОД(24,20) = 2*НОД(12,10)=2*2*НОД(6,5)=4*НОД(6/2,5)=4*НОД(3,5)=4*НОД(3,5-3)=4*НОД(3,2)=4*НОД(3-2,2)=4*НОД(1,2)=4*НОД(1,2-1)=4*НОД(1,1)

4. НОД(4859598, 3198268) в языке программирования Python бинарным алгоритмом Евклида.

(См. код в п.2)

Результат выполнения программы: