
- •Расчет пусковых и тормозных сопротивлений
- •Графоаналитический расчет ступеней пусковых сопротивлений
- •Расчет переходных процессов при пуске в семь ступеней
- •Динамическое торможение
- •Расчет сопротивления динамического торможения
- •Расчет переходных процессов при динамическом торможении
- •Расчет переходных процессов при торможении противовключением
- •Расчет уставок реле
- •Дополнительное задание:
- •Расчет сопротивления динамического торможения
- •Расчет переходных процессов при динамическом торможении
МИНОБРНАУКИ РОССИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
«НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ им. Р.Е. АЛЕКСЕЕВА»
(НГТУ)
Кафедра «Электрооборудование, электропривод и автоматика»
Отчет по лабораторной работе №4
«КОНТАКТОРНАЯ СИСТЕМА УПРАВЛЕНИЯ ДВИГАТЕЛЕМ ПЕРЕМЕННОГО ТОКА С ФАЗНЫМ РОТОРОМ»
Дисциплина: СУЭМО
Выполнили:
Муравьев Владислав
Мукин Иван
Петухов Николай
Федоров Кирилл
Симагин Максим
Плешаков Максим
Проверил:
Соколов В.В.
Нижний Новгород
2022 г.
ЦЕЛЬ РАБОТЫ: изучение принципов контакторного управления двигателем переменного тока с фазным ротором. В качестве управляемого взят двигатель МТО11-6.
ТЕХНИЧЕСКИЕ ДАННЫЕ АСИНХРОННОГО ДВИГАТЕЛЯ МТО11-6
Номинальная мощность - РН = 1,4 кВт;
Номинальная скорость вращения - nН = 885 об/мин;
Перегрузочная способность - = ММАКС/МН = 2,3;
Номинальный момент - MН = 15 Нм;
Номинальный ток статора при соединении звездой - ICН= 5,3 А;
Ток холостого хода - ICХ = 3,9 А;
Активное сопротивление обмотки фазы статора - RС = 5,98 Ом;
Индуктивное сопротивление обмотки фазы статора - хС= 3,93 Ом;
Номинальная ЭДС ротора - ЕРН= 112 В;
Номинальный ток ротора - IРН = 9,3 А;
Активное сопротивление фазы ротора - RР = 0,695 Ом;
Индуктивное сопротивление фазы ротора - хР= 0,5 Ом;
Коэффициент трансформации напряжения - КЕ= 3,14;
Момент инерции ротора - J= 0,0212 кг· м2,
Пусковой момент двигателя - М1= 4 Нм,
Момент сопротивления на валу -Мс = 0, 6 Нм.
Число пусковых (тормозных) ступеней - m =7
Расчет пусковых и тормозных сопротивлений
Особенностью
данной лабораторной установки является
то, что статор двигателя подключается
на пониженное напряжение питания (в
 раз
меньше номинального). Обмотки статора
двигателя соединены в звезду и на них
подано линейное напряжение UЛ
= 220 В, а не 380 В, поэтому при завершении
реостатного пуска двигатель работает
на искусственной механической
характеристике. Кроме того, максимальный
момент двигателя при пуске и торможении
принимается значительно меньше
допустимого (М1=4 Нм). Это сделано для
растягивания исследуемых переходных
процессов во времени и получения
наглядных осциллограмм пуска,
торможения и реверса.
раз
меньше номинального). Обмотки статора
двигателя соединены в звезду и на них
подано линейное напряжение UЛ
= 220 В, а не 380 В, поэтому при завершении
реостатного пуска двигатель работает
на искусственной механической
характеристике. Кроме того, максимальный
момент двигателя при пуске и торможении
принимается значительно меньше
допустимого (М1=4 Нм). Это сделано для
растягивания исследуемых переходных
процессов во времени и получения
наглядных осциллограмм пуска,
торможения и реверса.
Завершается разгон на искусственной механической характеристике. Построим естественную и искусственную (из за пониженного напряжения) характеристики двигателя.
Определим критический момент на естественной характеристике:

Определим
критический момент на искусственной
характеристике. Так как критический
момент асинхронного двигателя
пропорционален квадрату приложенного
напряжения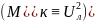 ,
то:
,
то:

Критическое скольжение двигателя в общем случае определяется из выражения:

Видно, что критическое скольжение зависит только от сопротивлений статора и ротора и не зависит от приложенного напряжения, поэтому при
отсутствии добавочных сопротивлений в цепи ротора:
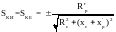
Рассчитаем активное сопротивление ротора, приведенное к статору:

Рассчитаем индуктивное сопротивление фазы ротора, приведенное к статору:

Определим критическое скольжение на естественной и искусственной характеристиках при отсутствии добавочных сопротивлений в цепи ротора:

Механические характеристики при отсутствии добавочных сопротивлений в цепи ротора строятся по формуле Клосса:

где

Скорость идеального холостого хода равна:
 ;
;
 104,719.
104,719.
На рис.1 приведены механические характеристики двигателя (естественная и искусственная при пониженном напряжении на статоре и отсутствии в цепи ротора добавочных сопротивлений).
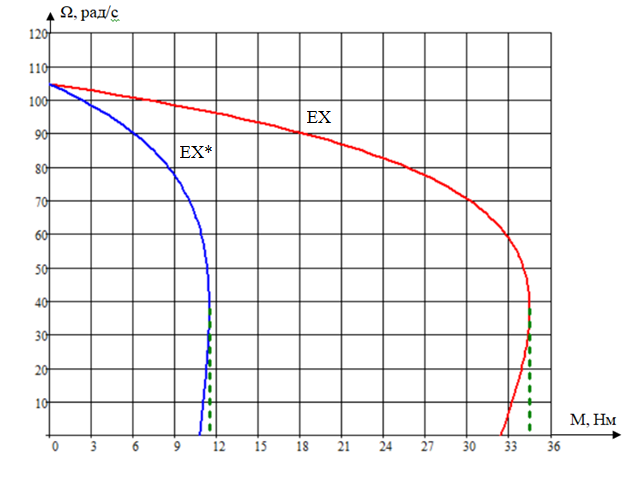
Рис.1 - Механические характеристики асинхронного электродвигателя (естественная механическая характеристика (ЕХ) и искусственная при пониженном напряжении и без добавочных сопротивлений в цепи ротора, которую в дальнейшем будем считать (ЕХ*))
Графоаналитический расчет ступеней пусковых сопротивлений
При использовании этого метода необходимо построить пусковые механические характеристики двигателя. Из рис. 1 видно, при М ≤ 4 Нм пусковые характеристики можно считать линейными. Для определения момента переключения М2 (М1/М2= λ1) необходимо рассчитать коэффициент λ1:

m=7 – число ступеней пуска
 – относительное
значение пускового момента в долях от
базисного;
– относительное
значение пускового момента в долях от
базисного;
 - базисные значения
скольжения и момента.
- базисные значения
скольжения и момента.
За
базисное значение момента примем
пусковой момент
 .
.
За
базисное значение скольжения примем
 ( S1
- это
скольжение на искусственной характеристике
без добавочных сопротивлений в цепи
ротора, при котором момент двигателя
равен пусковому М1=4
Нм).
( S1
- это
скольжение на искусственной характеристике
без добавочных сопротивлений в цепи
ротора, при котором момент двигателя
равен пусковому М1=4
Нм).
Для определения S1 подставим в формулу Клосса значения моментов (М1 и Мки), критического скольжения Sки и параметра а и получим:

После преобразований имеем:




 .
.
Получили
квадратное уравнение, решение которого
дает два действительных корня
 и
и

Выбираем

Тогда коэффициент λ1 при пуске в семь ступеней равен:

Рассчитаем
момент переключения М2,
который должен удовлетворять условию

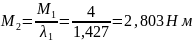
Значение
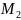 удовлетворяет
условию
,
где
удовлетворяет
условию
,
где
 =0.6
=0.6

На рис. 2 приведены линейные аппроксимации механических характеристик двигателя при пуске в семь ступеней. Сначала были построены лучи, выходящие из точки Ω0 (скорости идеального холостого хода) и проходящие при М=М1=4 Нм через точки с S=S1 и S=0 - т.е. были построены искусственные механические характеристики, на которых начинается (ИХ1) и заканчивается (ИХ3) пуск двигателя. Положение ИХ2 легко определяется при рассчитанном значении момента М2.
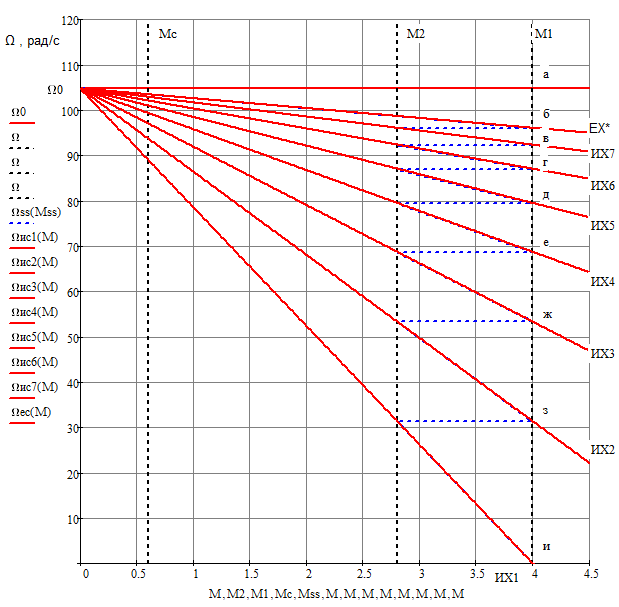
Рисунок 2- Механические характеристики двигателя при пуске в семь ступеней
Вывод: при М1=4 Нм характеристики двигателя можно считать линейными, поэтому графики строим в виде прямых линий.
По построенным пусковым характеристикам можно определить как величины добавочных сопротивлений, включаемых в ротор на каждой ступени пуска, так и величины полных сопротивлений в роторе на каждой ступени. Так добавочные сопротивления при семиступенчатом пуске определяются из соотношений:






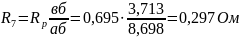
а полные сопротивления в фазе ротора равны:
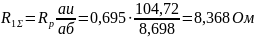
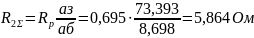
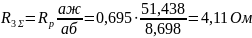




Аналитический расчет пусковых ступеней
В общем случае
ступени пусковых сопротивлений и полные
активные сопротивления фаз ротора
определяются из выражений:
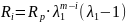 и
и
 соответственно.
соответственно.
При пуске в семь ступеней величины добавочных пусковых сопротивлений соответственно равны:
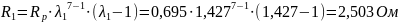






Величины полных активных сопротивлений фазы ротора равны:







