1.4. Движение тела в жидкости

Воздействие жидкой или газообразной среды на тело, движущееся в ней с постоянной скоростью v, будет таким же, каким было бы действие на неподвижное тело набегающего на него со скоростью v однородного потока жидкости или газа. Следовательно, при выяснении действующих на тело сил безразлично, что считать движущимся – тело или среду. Удобно предполагать тело неподвижным, а среду движущейся.

Силу F, с которой набегающий поток действует на тело, можно разложить на две составляющие: направленную вдоль скорости v невозмущенного потока силу X, называемую лобовым сопротивлением, и перпендикулярную к v силу Y, называемую подъемной силой. Лобовое сопротивление складывается из сил давления и сил внутреннего трения. Очевидно, что на тело, симметричное относительно направления скорости потока v, может действовать только лобовое сопротивление, подъемная сила в этом случае будет отсутствовать.

Покажем отсутствие лобового сопротивления на примере обтекания идеальной жидкостью очень длинного (бесконечного) цилиндра (Рисунок 1.2).

Рис. 1.2. Обтекание идеальной жидкостью очень длинного (бесконечного) цилиндра

Т.к. идеальная жидкость не обладает вязкостью, то она должна скользить по поверхности цилиндра, полностью обтекая его. Поэтому линии тока должны быть симметричными как относительно прямой, проходящей через точки 1 и 3, так и относительно прямой, проходящей через точки 2 и 4. Теорема Бернулли позволяет по картине линий тока судить о давлении в разных точках потока. Вблизи точек 1 и 3 давление одинаково (больше, чем в невозмущенном потоке, так как скорость вблизи этих точек меньше). Вблизи точек 2 и 4 давление тоже одинаково (меньше, чем в невозмущенном потоке, так как скорость вблизи этих точек больше). Следовательно, результирующая сил давления будет равна нулю. Такой же результат получается для тел любой (в том числе и несимметричной) формы. Этот вывод касается только лобового сопротивления. Подъемная сила, равная нулю для симметричных тел, для несимметричных тел отлична от нуля.

На рисунке 1.3 показаны линии тока при обтекании идеальной жидкостью полуцилиндра. Вследствие полного обтекания линии тока симметричны относительно прямой, проходящей через точки 2 и 4. Но относительно прямой, проходящей через точки 1 и 3, картина линий тока несимметрична.

Рис. 1.3. Линии тока при обтекании идеальной жидкостью полуцилиндра

Вблизи точки 2, где линии гуще, давление меньше, чем вблизи точки 4, в результате чего возникает подъемная сила.

Иначе обстоит дело при движении тела в вязкой жидкости. В этом случае очень тонкий слой жидкости прилипает к поверхности тела и движется с ним как одно целое, увлекая за собой из-за внутреннего трения последующие слои. По мере удаления от поверхности тела скорость слоев становится все меньше и, наконец, на некотором расстоянии от поверхности жидкость будет не возмущенной движением тела. Таким образом, тело оказывается окруженным слоем жидкости с быстро изменяющейся внутри него скоростью. Этот слой называется пограничным. В нем действуют силы вязкого трения, которые, в конечном счете, приложены к телу и приводят к возникновению лобового сопротивления.

Но влияние вязкости не исчерпывается возникновением сил трения. Наличие пограничного слоя изменяет характер обтекания тела жидкостью. Полное обтекание становится невозможным. Действие сил трения в пограничном слое приводит к тому, что поток отрывается от поверхности тела, в результате чего позади тела возникают вихри (Рис. 1.4).

Рис. 1.4. Появление вихрей

Вихри уносятся потоком и постепенно затухают вследствие трения. При этом энергия вихрей расходуется на нагревание жидкости. Давление, в образующейся за телом вихревой области оказывается пониженным, вследствие чего результирующая сил давления отлична от нуля. Это обуславливает лобовое сопротивление.

Таким образом, лобовое сопротивление складывается из сопротивления трения и сопротивления давления. При данных поперечных размерах тела сопротивление давления сильно зависит от формы тела. Наименьшим сопротивлением давления обладают тела хорошо обтекаемой каплевидной формы.

Рис. 1.5. Обтекание жидкостью тела каплевидной формы

Соотношение между сопротивлением трения и сопротивлением давления определяется значением числа Рейнольдса.

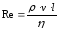_(1.10)

В данном случае v – скорость тела относительно жидкости, l – характерный размер тела (радиус для тела шаровой формы). При малых Re (т.е. при малых v и l) основную роль играет сопротивление трения, так что сопротивлением давления можно пренебречь. С ростом вязкости относительная роль сил трения возрастает. По мере увеличения Re роль сопротивления давления все больше возрастает. При больших значениях Re в лобовом сопротивлении преобладают силы давления.

Число Рейнольдса служит и здесь критерием подобия. Оно определяет характер сил, действующих на тело в потоке жидкости. Это используется в моделировании. Например, модель самолета ведет себя в потоке газа так же, как и её прообраз, если кроме геометрического подобия модели и самолета будет соблюдено равенство для них значений числа Рейнольдса. [4]

Стокс установил, что при небольших скоростях и размерах тел (т.е. при малых Re, когда сопротивление среды обусловлено только силами трения), модуль силы сопротивления определяется формулой

. (1.11)

Здесь η – динамическая вязкость среды, v – скорость движения тела, l – характерный размер тела, k – коэффициент пропорциональности, который зависит от формы тела. Для шара, если взять в качестве l его радиус r, коэффициент пропорциональности равен 6π. Следовательно, сила сопротивления движению в жидкостях небольших шариков при малых скоростях равна

(1.12)

Нужно иметь в виду, что формула Стокса справедлива при условии, что расстояние от тела до границ жидкости (до стенок сосуда) намного больше размеров тела. [5]