1. Вязкость и реология

Ньютон пришел к изучению течения жидкостей, когда пытался моделировать движение планет Солнечной системы посредством вращения цилиндра, изображавшего Солнце, в воде. В своих наблюдениях он установил, что если поддерживать вращение цилиндра, то оно постепенно передастся всей массе жидкости. Результаты своих наблюдений он подробно отразил в трактате «О круговом движении в жидкостях» (1687 г.). Рассматривая эти явления, доступные непосредственному наблюдению, Ньютон приписывал их «недостатку скольжения» между частицами жидкости и использовал термин трение. Впоследствии для описания подобных свойств жидкостей стали использовать термины «внутреннее трение» и «вязкость», получившие одинаковое распространение. Исторически, эти работы Ньютона положили начало изучению вязкости и реологии.

Дальнейшее развитие реология получила в работах Пуазейля, выполненных в середине XIX века с целью изучения закономерностей течения крови в сосудах. Для упрощения экспериментов Пуазейль моделировал течение воды в стеклянных трубках. Эти работы и привели его к открытию закона, впоследствии названного его именем. Он установил, что количество воды, протекающей по трубке, прямо пропорционально четвертой степени диаметра трубки и первой степени давления. В том же XIX веке благодаря Бернулли, Дарси, Кулону, Навье, Стоксу, Шведову были выполнены важные работы по изучению вязкости. С тех пор все большее число исследователей занимается проблемами вязкости и реологии, в связи с их большой значимостью для практики. В нашей стране труды в области вязкости и реологии связаны с М.П. Волоровичем, М.М. Кусаковым, П.А. Ребиндером, Г.И. Фуксом и многими другими исследователями.

В настоящее время структурно-механические свойства тел и сред исследуют методами реологии – науки о деформациях и течении материальных систем. Сам термин «реология» появился в середине тридцатых годов ХХ века. Собственно, реология изучает механические свойства систем по проявлению деформации под действием внешних напряжений. Методы реологии широко используются для исследования молекулярной структуры и описания вязких свойств самых различных систем.

1.1. Вязкость жидкости по теории Френкеля

В 1925 г. Я.И. Френкель на основе молекулярно-кинетических представлений предложил объединить такие свойства тел, как текучесть и твердость. Результаты его работы подробно представлены в монографии «Кинетическая теория жидкостей», впервые вышедшей в 1945 г.

Рассмотрим несколько упрощенный вывод формулы вязкости для жидкостей на основе представлений молекулярно-кинетической теории Френкеля. В жидкостях расстояния между молекулами значительно меньше, чем в газах, поэтому на движение молекул в жидкости в первую очередь влияет межмолекулярное взаимодействие, ограничивая их подвижность. Рассмотрим отдельную молекулу жидкости и будем считать, что она находится в силовом поле, которое создано окружающими ее молекулами. Это поле представим как совокупность большого числа потенциальных «ямок» - минимумов потенциальной энергии, - расположенных друг от друга на расстоянии того же порядка, что и размеры молекулы. Такой потенциальный рельеф, в котором движется молекула жидкости, в одномерном случае можно аппроксимировать зубчатой линией (см. рисунок 1.1).

Рис. 1.1. Схема потенциального поля, в котором движется молекула жидкости.

Высота зубцов рельефа определяет кинетическую энергию, которая требуется частице для «перескока» из своей потенциальной ямки в одну из соседних. Будем считать, что эту энергию она приобретает за весьма короткое время t₀, в течение которого частица перескакивает расстояние δ₂, отделяющее соседние «ямки». После перескока частица отдает эту энергию и застревает в новой «ямке» в среднем на время t. Времена t и t₀ можно связать между собой. Время пребывания частицы в каком-либо состоянии пропорционально вероятности этого состояния, определяемой значением потенциальной энергии Е_р по формуле Больцмана. Отсюда для отношения времен t и t₀ имеем

(1.1)

где Т – температура жидкости; k – постоянная Больцмана; ∆Е_р = Е_р2 - Е_р1; ∆V₁ и ∆V₂ – элементы объема, соответствующие участкам δ₁ и δ₂ на рис 1. Если считать их равными, то

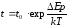(1.2)

Установить точное значение t₀ оказывается невозможным. Приближенные оценки показывают, что время t₀ имеет порядок 10^-13с и приблизительно совпадает с периодом колебаний молекулы жидкости в стационарном состоянии.

Обсудим в рамках рассматриваемой нами модели зависимость вязкости от температуры. Будем считать, что перескок частицы из одного состояния в другое совершается со средней тепловой скоростью частицы, определяемой соотношением:

<v> = , (1.3)

где m – масса частицы. Тогда, по аналогии с газом, по (1.2) и (1.3), средняя «длина свободного пробега» молекул жидкости

λ= <v> t = t₀ exp. (1.4)

Воспользуемся теперь рассуждениями, которые используют при выводе выражения для динамической вязкости η газов, тогда

η=(1/3) nm<v>λ , (1.5)

где n – число молекул в единичном объеме. Подстановка (1.4) в (1.5) приводит к следующему выражению для вязкости жидкости:

(1.6)

Формула (1.6) находится в удовлетворительном согласии с экспериментальными данными и в настоящее время является самой используемой. При kT < ∆Е_р из (1.6) следует, что вязкость жидкости уменьшается при повышении температуры (в противоположность газам). Однако при достаточно больших температурах, когда kT > ∆Е_р (при kT = ∆Е_р вязкость, как это видно из (1.6), имеет минимум), вязкость начинает возрастать с температурой, так же как и в случае газов [1].