Панков Пособие по АСП

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждениевысшего образования

Московский технический университет связи и информатики

К.Н. Панков

АНАЛИЗ СЛУЧАЙНЫХ ПРОЦЕССОВ

Учебное пособие

для обучающихся в бакалавриате по направлении. 11.03.02 - Инфокоммуникационные технологии и системы связи

Москва 2021

Панков К.Н. Анализ случайных процессов. Учебное пособие / МТУСИ. – М., 2021. - 77 с.

В данном учебном пособии рассмотрены основные понятия, теоремы и методы теории случайных процессов и их применение. Дана классификация случайных процессов, теория цепей Маркова с непрерывным и дискретным временем. Значительную часть курса занимает изложение теории систем массового обслуживания (СМО). Приведена классификация СМО, рассмотрены показатели качества обслуживания и эффективности работы СМО, разобраны примеры анализа работы различных СМО. Теоретический материал изложен с многочисленными примерами.

Учебное пособие ориентировано на обучающихся в бакалавриате по направлению подготовки 11.03.02 - Инфокоммуникационные технологии и системы связи.

Ил. __, табл. __, список лит.__ назв.

Издание утверждено Методическим советом университета в качестве учебного пособия. Протокол No __от __.__.____г.

Рецензенты:

© Московский технический университет связи и информатики, 2021

2

Введение

Теория случайных процессов – бурно развивающаяся область теории вероятностей, изучающая изменение во времени состояния стохастической системы. Случайные процессы находят широчайшее применение в таких областях науки и техники, как автоматизированные системы управления, автоматизация технологических процессов и производств, радио- и электротехника, кибернетика, биология, химия, экономика, транспорт, связь и т.п. Программы все большего числа специальностей и направлений подготовки инженеров включают курс случайных процессов. Для успешного освоения дисциплины необходимы базовые знания курсов «Высшая математика» и «Теория вероятностей и математическая статистика», а также некоторые элементы курсов «Математический анализ», «Дифференциальные уравнения», «Функциональный анализ». Данное издание предназначено для методического обеспечения направления подготовки 11.03.02 – Инфокоммуникационные технологии и системы связи, но также может быть использовано студентами других специальностей, предусматривающих изложение данного предмета

3

Тема № 1 Элементы теории множеств, комбинаторики и теории меры

Тема № 1 Основные понятия. Стационарные процессы

Рассмотрим произвольное вероятностное пространство ,A, . Вспомним

определение из курса теории вероятностей, призванное формально определить величины, подлежащие «измерению» в случайных экспериментах.

Определение. Случайной величиной называется функция w : ,

заданная на пространстве элементарных событий , принимающая значения в

и удовлетворяющая условию, что для любого вещественного х множество

w : w x является событием, т.е. w : w x A.

Часто при исследовании различных явлений в области телекоммуникаций приходится иметь дело со случайными величинами, изменяющимися во времени.

Основным понятием теории случайных процессов является следующее.

Определение. Случайным процессом (или случайной функцией) t ,t T

называется семейство случайных величин t , зависящих от параметра t, пробегающего некоторое множество значений T . Таким образом, любому фиксированному t0 однозначно ставится в соответствие случайная величина t0 ,

называемая сечением случайного процесса. При этом считается, что все случайные величины t , которые образуют это семейство, заданы на одном

вероятностном пространстве ,A,P .

Обычно параметр t играет роль времени (так сложилось исторически, из практических потребностей прикладных наук). В пособиях по теории случайных процессов, связанных с их инженерными приложениями, вместоt ,t T или просто t часто используется обозначение X(t).

Определение. Реализацией, выборочной функцией или траекторией

.

На практике считается, что в результате некоторого эксперимента происходит элементарное событие 0 и наблюдается значение t t в

точке 0 . Поэтому траектория случайного процесса зависит от наблюдений при эксперименте. Иначе говоря, реализацией случайного процесса X(t) называется неслучайная функция x(t), в которую превращается случайный процесс X(t) в результате опыта; другими словами, конкретный вид, принятый случайным процессом X(t), который наблюдался на каком-то отрезке времени от 0 до τ.

4

полной и исчерпывающей характеристикой случайной величины t . Эта

процесса t ,t T .

Пример. Пусть T . По определению зададим t t t0 b, где t0,b

- некоторые фиксированные числа, - некоторая случайная величина, заданная на некотором вероятностном пространстве ,A,P , не зависящая от

Тангенс угла наклона этой линии равен значению 0 . Так как случайная величина может принимать разные значения то все реализации (траектории) случайного процесса t будут принадлежать пучку прямых на плоскости. Каждая прямая этого пучка проходит через точку плоскости с координатамиt0,b . Эта точка в аналитической геометрии носит название центра пучка прямых на плоскости.

5

Случайный процесс t в данном примере носит называние веерного случайного процесса.

Является ли одномерный закон распределения полной и исчерпывающей характеристикой случайного процесса? Очевидно, нет. Эта функция характеризует только свойства одного отдельно взятого сечения случайного процесса, но не дает понятия о совместном распределении двух (или более) сечений процесса. Иначе говоря, зная поведение случайного процесса в момент времени t, мы не можем предсказать поведение значений t в другие моменты времени. Для описания этих зависимостей необходимо рассмотреть функцию

распределения случайного вектора t1 ,..., tn , координаты которого равны значениям процесса в моменты времени t1,...,tn .

Обозначим

Ft1,...,tn (x1,...,xn) F t1 ,..., tn (x1,...,xn) F (x1,...,xn ) P t1 x1,..., tn xn .

Определение. Семейство функций

Ft1,...,tn (x1,...,xn), n , t1,...,tn Tn,ti tj

называется семейством конечномерных распределений случайного процесса

t ,t T .

Это семейство удовлетворяет условиям согласованности:

математическим ожиданием случайного процесса.

6

2. Пусть D t D t =E t m t 2 для всех t T , если дисперсия определена и конечна, тогда D t :T - дисперсия случайного процесса.

Наряду с дисперсией в инженерных приложениях теории случайных процессов часто рассматривается функция среднеквадратичного отклонения

t D t :T .

3. Пусть m t , m s , тогда K s,t E s m s t m t -

ковариационная функция случайного процесса. Синонимами понятия ковариационная функция в технической литературе являются автоковариационная и автокорреляционная функции. Согласно мнению ряда ученых наиболее удачным названием является «автоковариационная функция», подчеркивающее, что речь идет о ковариации двух сечений одного и того же процесса (от латинского autos – сам, направленный на самого себя).

Докажите следующие свойства K s,t :

а) K s,t 2 D s D t ,

б) K t,t D t ,

в) K s,t K t,s .

нормированная автоковариационная, нормированная автокорреляционная) функция случайного процесса.

Докажите следующие свойства R(s,t):

а) R s,t 1,

б) R t,t 1,

в) R s,t R t,s .

требуется найти функцию распределения сечения этой функции, математическое ожидание mX (t), дисперсиюDX (t), среднеквадратичное отклонение X (t) и корреляционную функцию K X (t1,t2).

Согласно определению функции распределения случайной величины

FX (t) x P X(t) x P Ut2 2 x

.

7

Далее рассмотрим случай, когда t 0. Так как U N(2; 4),то

По определению

mX (t) E X t E Ut2 2 t2 EU 2,

DX (t) DX t D Ut2 2 t4 DU ,

X (t) 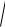DX t t2 DU ,

K X t1,t2 E X t1 mX t1 X t2 mX t2

E Ut12 2 t12 EU 2 Ut22 2 t22 EU 2 t12t22 DU .

Параметры нормального распределения являются его основными числовыми характеристиками (EU 2,DU 4). Следовательно,

mX (t) 2t2 2, DX (t) 4t4 ,X (t) 2t2 ,

K X t1,t2 4t12t22 .

Классификация случайных процессов

Основными признаками, по которым можно провести классификацию

процесса.

Если E – это некоторый непрерывный промежуток из , то E – фазовое пространство действительного случайного процесса.

2). Временной параметр T .

Определение. Если t T , то говорят, что процесс t ,t T является

процессом с дискретным временем. Если параметр t принимает все значения из некоторого непрерывного промежутка на числовой прямой, то говорят, что процесс t ,t T - случайный процесс с непрерывным временем.

t2 t1 ,..., tn tn 1 .

8

Случайный процесс называется процессом с независимыми приращениями,

если величины t2 t1 ,..., tn tn 1 независимы в совокупности.

Случайный процесс называется процессом с некоррелированным

случайные величины.

Случайный процесс называется процессом с ортогональным приращением,

Случайный процесс называется марковским, если при всех n для любых

переходных вероятностей марковского процесса.

Данная функция играет важную роль при изучении подобных процессов.

Стационарные процессы

Рассмотрим случайный процесс t ,t T .

Определение. Случайный процесс называется стационарным в узком

Определение. Случайный процесс называется стационарным в широком смысле, если:

K s,t K s h,t h , т.е. K s,t зависит только от разности t и s.

Проверьте, всегда ли из стационарности в узком смысле следует стационарность в широком смысле.

Для стационарного в широком смысле процесса корреляционная функция R s,t зависит только от разности t s и может быть обозначена

R s,t R t s R . Это верно и для ковариационной функции

K s,t K t s K

Важную роль при изучении стационарных в широком смысле случайных процессов играет следующая

Теорема (Бохнера-Хинчина – без доказательства). Пусть t ,t T -

стационарный в широком смысле случайный процесс, корреляционная функция которого R непрерывна. Тогда существует случайная величина с

9

функцией распределения F x F x , характеристическая функция которой равна R , т.е. R .

По теореме единственности такая функция F x определяется однозначно.

Ответим на вопрос, когда данный случайный процесс является стационарным в широком смысле и найдем корреляционную функцию R(s,t).

m(t) E 1 cos(wt) E 2 sin(wt), т.е. для того, чтобы m(t) не зависело от t, необходимо, чтобы E 1 E 2 0.

Пусть s t . Тогда

K s,t E t s E 12 cos wt cos ws 22 sin wt sin ws

1 2 cos wt sin ws 1 2 sin wt cos ws E 12 cos wt cos ws

E 22 sin wt sin ws E 1 2 sin t s w .

то, следовательно, случайные величины 1 и 2 не коррелированны. Более того, мы будем считать, что они независимы.

Следовательно,

K(s,t) 2 cos wt cos ws sin wt sin ws 2 cos w t s 2 cos w .

10