Квантово-механическое описание физических свойств атомно-молекулярных объектов живых систем / Квантово-механическое описание физических свойств атомно-молекулярных объектов живых систем

12

Квантово-механическое описание физических свойств атомно-молекулярных объектов живых систем

[S1] В конце 19 – начале 20 века физика претерпевала кризис, связанный с появившимися новыми проблемами: ультрафиолетовая катастрофа, фотоэффект, радиоактивность, линейчатый спектр излучения и поглощения атома водорода и другие, которые было не понятно, как решать. Существовавшая к началу этого периода физика для большинства физиков казалась стройной моделью описания природы, которая позволяла решать насущные проблемы тех времён. Она не вызывала сомнений в своей истинности и было трудно представить, что её подходы, возникавшие на протяжении веков, в какой-то момент дадут сбой и перестанут столь стройно и логично описывать окружающий мир.

Тем не менее нужно было что-то делать с возникшими проблемами, решение которых лежало в пересмотре базовых принципов и постулатов. Начавшийся пересмотр положил начало науке, которая смогла предоставить решение этих проблем тем самым изменив наше понимание об устройстве мира радикальным образом. Сначала эта наука называлась квантовой теорией, подчёркивая тем самым свою начальную стадию развития, затем с проведением новых исследований, она перешла в статус целого новой дисциплины – квантовой механики, а теперь это большой раздел современной физики, называемый квантовой физикой наряду с другими дисциплинами, использующими её подходы, например квантовая химия и квантовая биология.

Квантовая механика – это фундаментальная теория в физике, которая даёт описание физических свойств природы в масштабе атомов и субатомных частиц.

[S2] Точно сказать, когда было положено начало зарождения квантовой механики, довольно трудно, поскольку идеи квантового, дискретного описания природы высказывались ещё в античной Греции в форме атомистического учения Левкиппа и его ученика Демокрита, представления которых нашли своё отражение в философской поэме римского поэта Тита Лукреция Кара «О природе вещей».

[S3] Условно за начало зарождения квантовой теории можно принять начало XIX века, когда химические исследования Джона Дальтона и Амедео Авогадро придали вес атомной теории материи, идею, которую Джеймс Клерк Максвелл, Людвиг Больцман и другие развили, создав кинетическую теорию газов. Её успехи придали дополнительную убедительность идее о том, что материя состоит из атомов. К тому же в 1838 году Майкл Фарадей открыл катодные лучи, а в 1897 год Джозефом Джоном Томсоном был открыт электрон – элементарный носитель заряда.

В 1877 году Людвиг Больцман предположил, что энергетические уровни физической системы, такой как молекула, могут быть дискретными (а не непрерывными). Обоснование Больцманом наличия дискретных энергетических уровней в молекулах, таких как газообразный йод, берет своё начало в его теориях статистической термодинамики и статистической механики и подкрепляется математическими аргументами, как это произошло двадцать лет спустя с первой квантовой теорией, выдвинутой Максом Планком.

[S4] В 1900 году немецкий физик Макс Планк, который никогда не верил в дискретные атомы, неохотно ввёл идею, также её называют гипотезой или постулатом Планка, о том, что энергия, переносимая излучением и излучаемая телом, квантуется, чтобы вывести формулу для наблюдаемой частотной зависимости энергии, излучаемой черным телом, названную законом Планка разрешив тем самым ультрафиолетовую катастрофу. Таким образом Макс Планк показал, что энергия колеблющихся атомов и молекул может принимать не любые, а только некоторые определённые значения. Энергия излучается не непрерывно, а некоторыми порциями, которые Планк назвал квантами энергиями или, просто, квантами (от лат. quantum (ед. ч.), quanta (мн. ч.), от лат. quantus – сколько, как много). Энергия одного кванта излучения пропорциональна частоте излучения, где коэффициентом пропорциональности выступает постоянная Планка – в этом выражении и состоит гипотеза Планка.

[S5] В 1905 году Альберт Эйнштейн использовал кинетическую теорию для объяснения броуновского движения, обосновав теоретически существование молекул. Позже это обоснование подтвердится экспериментально. Также в 1905 году Эйнштейн объяснил фотоэлектрический эффект, предположив, что свет, или, в более общем смысле, все электромагнитное излучение, существует в пространственно локализованных пакетах, то есть его можно разделить на конечное число «квантов энергии (действия)» или «квантов света» (нем. Lichtquanta), которые являются локализованными частицами в пространстве. Эйнштейну удалось получить основное уравнение, описывающее фотоэффект, которое получило название «уравнение А. Эйнштейна для фотоэффекта». Эти кванты энергии позже стали называть фотонами.

[S6] После этого были начаты исследования по выявлению «кирпичиков вещества» – атомов, которые начались с экспериментов Эрнеста Резерфорда по рассеянию альфа-частиц. Из этих экспериментов выяснилось, что в веществе существуют очень сильные электрические поля, которые создаются очень малыми, но массивными зарядами, которые Резерфорд назовёт ядрами атомов, вокруг которых вращаются лёгкие электроны. После него предлагались другие модели атомов, эволюция которых приведена на слайде [S7]. Одной из важных таких моделей была модель Нильса Бора.

[S8] Для того, чтобы объяснить линейчатые спектры атома водорода Бор ввёл несколько постулатов, на основании которых описывалось поведение атомов.

Первый постулат – атом может находиться только в дискретных устойчивых состояниях, характеризуемых определёнными дискретными значениями энергии. В устойчивых состояниях атома электроны движутся вокруг ядра по определённым («дозволенным») орбитам, причём радиусы этих орбит соответствуют возможным значениям энергии атома. Орбиты же электронов определяются согласно правилу квантования Бора – Зоммерфельда: из всех возможных согласно классической механике орбит реализуются только те, у которых орбитальный момент импульса электрона равен произведению номера орбиты, на приведённую постоянную планка (постоянная Дирака). А значения энергию для случая водородоподобного атома боровская теория даёт формулу (слайд).

[S9] Второй постулат – при движении по дозволенным орбитам электроны – вопреки классической электродинамике – не излучают электромагнитных волн. Излучение может происходить только при переходе электрона с одной дозволенной орбиты на другую.

[S10] Третий постулат – испускание и поглощение энергии атомом происходит “скачками”, каждый из которых представляет собой порцию (квант энергии), кратную hν.

[S11] Следующим шагом, определившим современный вид квантовой механики, стало выдвижение в 1923 году французским физиком Луи де Бройлем гипотезы, а затем и теории волн материи. Гипотеза де Бройля состоит в том, что всем микрообъектам присущи одновременно и корпускулярные и волновые свойства – провозглашение так называемого корпускулярно-волнового дуализма. Идея де Бройля состояла в том, что подобно тому, как электромагнитная волна ассоциируется с фотоном, де Бройль допустил, что и каждой материальной частице сопоставлена волна, частота ν которой связана с энергией частицы соотношением 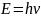, где h – постоянная Планка. Эта теория относилась к одной частице и вытекала из не менее революционной теории – специальной теории относительности. В результате чего было получено основное соотношение теории де Бройля: 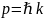, где p – импульс частицы-волны, а k – её волновой вектор; или ему эквивалентный вариант 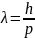, где λ – длина волны.

[S12] На основе подхода де Бройля в 1925 году родилась современная квантовая механика, когда немецкие физики Вернер Гейзенберг, Макс Борн и Паскуаль Йордан разработали матричную механику, а австрийский физик Эрвин Шрёдингер придумал волновую механику.

Матричная механика Гейзенберга начала зарождаться после его попыток рассчитать спектральные линии атома водорода. Проблему удалось решить путём модификации описания движения электрона с помощью рядов Фурье, через которые представляли волновое движение электрона в атоме, доставшееся ещё от де Бройля. Модификация заключалась в том, что на коэффициенты ряда Фурье налагались особые условия, а из этих элементов составлялись специальные матричные величины, которыми описывалось состояние атома и, в целом, квантово-механической системы.

[S13] У Шредингера был немного другой подход. Шредингер, как и Гейзенберг, занимался спектрами атомов. До него и до де Бройля в 1921 году Артур К. Лунн из Чикагского университета использовал тот же релятивистский подход чтобы вывести то, что мы сейчас называем соотношением де Бройля. К тому же Лунну удалось сформулировать дифференциальное уравнение, известное сейчас как уравнение Шредингера, и решить его для частного случая. На наработки Лунна не были представлены научному сообществу.

Развивая идеи де Бройля, физик Питер Дебай вскользь заметил, что если частицы ведут себя как волны, то они должны удовлетворять какому-то волновому уравнению. Вдохновлённый замечанием Дебая, Шредингер решил найти подходящее трёхмерное волновое уравнение для электрона. Он руководствовался аналогией между механикой и оптикой, проведенной Уильямом Роуэном Гамильтоном, которая заключалась в том, что предел нулевой длины волны в оптике напоминает механическую систему – траектории световых лучей становятся острыми треками, которые подчиняются принципу Ферма, аналогу принципа наименьшего действия.

Однако к тому времени Арнольд Зоммерфельд уточнил модель Бора с помощью релятивистских поправок. Шредингер использовал релятивистское соотношение энергии и импульса, чтобы найти то, что сейчас известно как уравнение Клейна-Гордона.

После Шредингер показал, что его нерелятивистская версия волнового уравнения даёт правильные спектральные энергии водорода в работе, опубликованной в 1926 году.

Уравнение Шредингера подробно описывало поведение пси-функции, но ничего не говорило о её природе. Шредингер пытался интерпретировать своё уравнение, как плотность заряда, а затем пересмотрел это предложение, заявив в своей следующей работе, что модуль квадрата пси-функции является плотностью заряда. Однако этот подход оказался неудачным. В 1926 году, всего через несколько дней после публикации этой работы, Макс Борн успешно интерпретировал пси-функцию как амплитуду вероятности, модуль квадрата которой равен плотности вероятности. Эта интерпретация используется и по ныне, являясь фундаментальным пониманием устройства микромира. Впоследствии Шредингер показал, что его подход и подход Гейзенберга эквивалентны.

[S14] После этих работ происходил процесс синтеза релятивистской теории с квантовой механикой, а также приведением квантовой механики в стройную и строгую науку занимался. Ключевыми в этом процессе оказались следующие лица. Поль Дирак начал процесс объединения квантовой механики со специальной относительностью, предложив уравнение Дирака для электрона. Он также стал пионером в использовании теории операторов, включая влиятельную нотацию Бра-кета. В тот же период венгерский эрудит Джон фон Нейман сформулировал строгую математическую основу квантовой механики в виде теории линейных операторов на гильбертовых пространствах. В современном виде постулаты квантовой механики выглядят следующим образом. Первый постулат – cостояние изолированной физической системы представлено в фиксированный момент времени t в виде вектора состояния 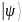принадлежащего гильбертовому пространству 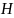, называемое пространством состояний. Гильбертово пространство составной системы – это тензорное произведение гильбертовых пространств состояний, связанных с составными системами. Для нерелятивистской системы, состоящей из конечного числа различимых частиц, составными системами являются отдельные частицы.

[S15] Второй постулат – каждая измеряемая физическая величина 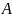описывается гермитианским оператором A, действующим в пространстве состояний . Этот оператор является наблюдаемым, что означает, что его собственные векторы образуют базис для . Результат измерения физической величины должен быть одним из собственных значений соответствующей наблюдаемой величины A.

Третий постулат – когда физическая величина измеряется на системе в нормализованном состоянии , вероятность получения собственного значения (обозначаемого 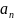для дискретных спектров и 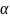для непрерывных спектров) соответствующей наблюдаемой величины A даётся квадратом амплитуды соответствующей волновой функции (проекция на соответствующий собственный вектор).

[S16] Четвёртый (постулат) – если измерение физической величины на системе в состоянии даёт результат , то состояние системы сразу после измерения является нормированной проекцией на собственное подпространство, связанное с .

Пятый (постулат) – временная эволюция вектора состояния 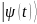определяется уравнением Шредингера, где 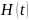– наблюдаемая величина, связанная с полной энергией системы (называемая гамильтонианом) – постулирование уравнения Шредингера.

Шестой эквивалентный пятому постулат – временная эволюция замкнутой системы описывается унитарным преобразованием начального состояния.

[S17] В дополнение к этим свойствам в квантовой механике постулируется ещё одна важная величина: все частицы обладают величиной, называемой спином – внутренним угловым моментом. Несмотря на название, частицы не вращаются буквально вокруг оси, и квантово-механический спин не имеет соответствия в классической физике.

Спин – это сохраняющаяся величина, которую несут элементарные частицы, а значит, составные частицы (адроны) и атомные ядра. Спин является одним из двух типов углового момента в квантовой механике, второй – орбитальный угловой момент. Спин 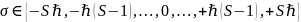, где 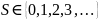– спиновое число.

Существование спинового углового момента электрона следует из экспериментов, таких как эксперимент Штерна-Герлаха, в котором наблюдалось, что атомы серебра обладают двумя возможными дискретными угловыми моментами, несмотря на отсутствие орбитального углового момента.

В дополнение к постулированию спина добавляется важный принцип исключения Паули, который гласит, что для (квантово-механической) системы из N частиц при любой перестановке двух частиц состояние системы меняется так, что выполняется равенство .

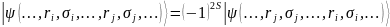[S18] Как уже было замечено ранее методы квантовой физики послужили основой для описания не простых физических систем, а для сложных химических и биологических систем. Ещё в первопроходцы в квантовой физике видели применение квантовой механики в биологических проблемах. В книге Эрвина Шредингера «Что такое жизнь?», опубликованной в 1944 году, обсуждалось применение квантовой механики в биологии. Шредингер представил идею «апериодического кристалла», который содержит генетическую информацию в конфигурации ковалентных химических связей. Он также предположил, что мутации возникают в результате «квантовых скачков». Другие пионеры Нильс Бор, Паскуаль Джордан и Макс Дельбрук утверждали, что квантовая идея дополнительности имеет фундаментальное значение для наук о жизни. В 1963 году Пер-Олов Лёвдин опубликовал туннелирование протонов как ещё один механизм мутации ДНК. В своей работе он заявил, что существует новая область исследований под названием «квантовая биология». В 1979 году советский и украинский физик Александр Давыдов опубликовал первый учебник по квантовой биологии под названием «Биология и квантовая механика».

Проблема применения квантовой механики к биологическим системам состоит в том, что эти системы состоят из гигантского количества частиц. Описание такой частицы будет сводиться к решению системы, составленной из уравнений Шредингера, каждое из которых описывает отдельную частицу, которая взаимодействует со всеми остальными, в простом случае, через электростатические силы. Вопрос решения такой системы относится к области математического анализа и математической физики и формулируется как задача о решении системы дифференциальных уравнений. В обще случае такие системы не решаются аналитически, поэтому пытаются найти приближенные решения и аппроксимации. Для этого прибегают к ряду упрощений и допущений.

В системах многих частиц гамильтониан принимает вид 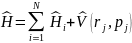, где 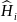– гамильтониан отдельной i-ой частицы; 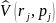– оператор потенциальной энергии, характеризующий так называемое спин-орбитальное взаимодействие. Этот оператор учитывает взаимодействие между спинами частиц и часть потенциальной энергии, зависящей от импульсов частиц и частично учитывающей запаздывание взаимодействия вследствие конечности скорости света. Взаимодействия, учитываемые этим слагаемым в нерелятивистском случае малы и могут быть учтены приближённо, например, по теории возмущений. Метод теории возмущений удобно применять тогда, когда рассматриваемая физическая система незначительно отличается от другой физической системы, для которой известно аналитическое решение уравнения Шредингера, тогда вводятся специальные поправки, которые могут с заданной точностью решать систему.

В многочастичную систему могут входить самые разнообразные частицы, но на практике чаще всего имеют дело с системами, состоящими из двух групп частиц, близких по своим характеристикам внутри группы и сильно отличающихся для частиц из двух различных групп. Например, молекула состоит из ядер атомов (одна группа тяжёлых частиц) и электронов (вторая группа лёгких частиц). Так же можно разделить на две группы частицы, составляющие твёрдое тело и так далее.

В такой системе характеристики движений частиц, принадлежащих к различным группам, существенно отличаются. Так, скорости движения ядер и электронов могут отличаться на несколько порядков. То же можно сказать и о характерных частотах процессов в коллективе ядер и в коллективе электронов.

В связи с этим можно приближённо считать, что, например, воздействие ядер атомов на движение электронов в молекуле или твёрдом теле (да и в отдельном атоме тоже) сводится к тому, что ядра создают практически стационарное поле, в котором движутся электроны.

Это означает, что в слагаемом гамильтониана – операторе, учитывающим спин-орбитальное взаимодействие мы пренебрегаем запаздыванием для взаимодействий ядро – электроны. Такое приближение называют адиабатическим.

Адиабатическое приближение основано на адиабатической теореме: физическая система остаётся в своём мгновенном собственном состоянии, если данное возмущение действует на неё достаточно медленно и если существует разрыв между собственным значением и остальной частью спектра гамильтониана.

(Условие адиабатического приближения следующее. Если при 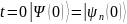для некоторого n, тогда если медленно изменять в диапазоне 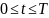, то в момент времени T будем иметь 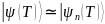вычислимую фазу.)

Также существует уравнение Лиувилля, которое описывает поведение системы частиц специального вида: .

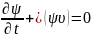[S19] Большинство биологических процессов основаны на протекании химических реакций, которые в свою очередь сводятся также к квантово-механическим механизмам.

Основной задачей квантовой химии является теоретическое описание и предсказание свойств и реакционной способности атомно-молекулярных систем путём решения уравнения Шредингера. Для молекул и атомов, содержащих более одного электрона, данное уравнение не решается строго, поэтому были развиты приближенные методы, среди которых самым наиболее предпочтительным стал метод самосогласованного поля. Идея этого метода физически очень проста. Предполагают, что в атоме каждый электрон, которому приписана собственная волновая функция, движется в суммарном кулоновском поле ядра и всех остальных электронов. Полная волновая функция всех электронов является произведением одноэлектронных волновых функций, а уравнение Шредингера превращается в систему интегро-дифференциальных уравнений, из которых определяются энергия и волновая функция. Оператор энергии включает кулоновские взаимодействия электрон–ядро и электрон – электрон.

Однако решения этой системы уравнений является непростым делом. Критерием точности здесь выступает минимум энергии системы, которого добиваются путём варьирования одноэлектронных волновых функций. В результате движение каждого электрона (его волновая функция) подстраивается под движение других электронов (под их волновые функции). Это называется методом самосогласованного поля. Он был разработан для атомов в 1927 г. Д. Хартрти.

В. А. Фок построил теорию самосогласованного поля для многоэлектронных систем с антисимметричными волновыми функциями и соответствующую систему обобщённых уравнений (их называют уравнениями Хартри – Фока):

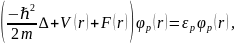
при этом оператор F (фокиан) выбирается так, чтобы он минимизировал соответствующее выражение для полной энергии многоэлектронной системы. Оператор фокиан учитывает кулоновские взаимодействия электрон – ядро и электрон – электрон (аналогично в уравнениях Хартри), а также самое главное – обменное взаимодействие электронов, то есть зависящий от спина кулоновский потенциал. Метод Хартри – Фока является мостом между квантовой механикой и химией.

[S20] Другими вариантами приближенного описания ядерно-электрон-электронных систем стали следующие квантово-химические теории: теория валентных связей, заложенная в 1927 г. В. Гейтлером и Ф. Лондоном в Германии, а в начале 30-х гг. развитая Дж. Слейтером и Л. Полингом в США; теория кристаллического поля, предложенная немецким учёным Х. Бете в 1929 г. и в последующие годы разрабатывавшаяся американским учёным Ван Флеком. [S21] Своё развитие она получила в 1950-е гг. благодаря исследованиям английского учёного Л. Оргела и двух датских учёных К. Йоргенсена и К. Бальхаузена. Она носит название теории поля лигандов. В конце 1920-х гг. была разработана теория молекулярных орбиталей (МО). Её основоположниками были Джон Леннард-Джонсон (Великобритания), Р. Малликен (США) и Ф. Хунд (Германия). В дальнейшем она развивалась многими другими исследователями. Все эти приближённые теории долгое время сосуществовали и дополняли друг друга.

Здесь на слайде [S22] показаны одноэлектронные обитали для водородоподобного атома, рассчитанные путём решения уравнения Шредингера.

[S23] Теория молекулярных орбиталей рассматривает молекулу как целое, а не как совокупность сохранивших индивидуальность атомов. В молекуле (как и в атоме) имеются дискретные энергетические состояния отдельных электронов (молекулярные орбитали) с их самосогласованным движением в поле друг друга и всех ядер молекулы.

Предполагается, что все электроны данной молекулы (как и в атоме) распределяются по соответствующим орбиталям. Состояние электрона в атоме описывается одноэлектронной волновой функцией ψ, являющейся решением уравнения Шрёдингера. Волновая функция ψ, зависящая от четырёх квантовых чисел, имеющая конкретный математический вид и удовлетворяющая условию нормировки и однозначности называется молекулярной орбиталью (МО) (по аналогии с атомной). Каждая орбиталь характеризуется своим набором квантовых чисел, отражающих свойства электронов в данном энергетическом состоянии. В отличие от одноц По аналогии с атомными s-, p-, d-, f- орбиталями молекулярные орбитали обозначают греческими буквами σ-, π-, δ-, φ-. МО образуются при комбинировании атомных орбиталей при достаточном сближении. Совокупность МО молекулы с указанием её типа и количеством электронов на ней даёт электронную конфигурацию молекулы. Существует 3 типа молекулярных орбиталей: связывающие, разрыхляющие и несвязывающие. Электроны на связывающих молекулярных орбиталях упрочняют связь, на разрыхляющих как бы дестабилизируют (расшатывают). Молекула является устойчивой лишь в том случае, если число электронов на связывающих орбиталях превышает число электронов на разрыхляющих. Электроны, находящиеся на несвязывающих молекулярных орбиталях, участия в образовании химической связи не принимают. Из n исходных атомных орбиталей возникает n МО. 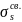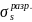Так, при образовании двухатомной молекулы H₂ из атомов водорода Н из их s-орбиталей возникают две двухцентровые МО — одна энергетически более выгодная (связывающая ), другая менее выгодная (разрыхляющая ), чем исходные атомные орбитали. На связывающей МО электрон большую часть времени пребывает между ядрами (повышается электронная плотность), способствуя их химическому связыванию. На разрыхляющей же МО электрон большую часть времени находится за ядрами, вызывая отталкивание ядер друг от друга.

Характер распределения электронов по МО определяет порядок (кратность) связи, её энергию, межъядерные расстояния (длина связи), магнитные свойства молекул и др. Заполнение молекулярных орбиталей подчиняется тем же правилам, что и заполнение атомных: принципу энергетической выгодности, принципу Паули, правилу Хунда, правилу Клечковского. В общепринятом приближении молекулярная орбиталь рассматривается как линейная комбинация атомных орбиталей (приближение МО ЛКАО).

Разработанные методы квантовой-механики уже применяются для описания процессов в живых системах. Так процесс фотосинтеза объясняется через возникновение связанной электронно-дырочной пары так называемого экситона, который передаёт свою энергию через явления квантовой когерентности.

Другим примером являются мутации ДНК. Их возможной причиной может быть квантовое туннелирование, когда в момент транскрипции нуклеотида он может спонтанно изменить свою форму. Вследствие этого изменённый нуклеотид теряет способность соединяться со своей первоначальной парой оснований, что приводит к изменению структуры и порядка нити ДНК.

На этом же эффекте строит теория обоняния.

Зрение также основано на взаимодействии фотона с органическими соединениями.

Видно, что квантовая-механика становится всё более обыденным инструментом описания биологических систем, становясь её мощным инструментом исследования.