РГРки https vk.com a777big / РГР6 https vk.com a777big.pdf

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральноегосударственноеавтономноеобразовательноеучреждениевысшегообразования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Инженерная школа энергетики Отделение электроэнергетики и электротехники

Направление: 13.03.02 Электроэнергетика и электротехника

Расчетно-графическая работа №6

Вариант – 173

по дисциплине:

ТОЭ 2.1

Томск-2022

Для одной фазы линии электропередачи длиной l=1500 км и удельными параметрами из таблицы 2 выполнить следующее:

1. В установившемся режиме при заданном фазном напряжении в конце линии

2( ) = √22 ( 314 + 2)

а) определить волновое сопротивление В, постоянную = + ,

фазовую скорость V, длину волны , комплексы действующих значений токов

I1 и I2, напряжения 1 = 1 1 , а также активные мощности в начале линии

P1 и конце линии P2, эффективность передачи энергии по линии (К.П.Д.) =

2;1

б) изменяя координату x от 0 до рассчитать распределение вдоль линии действующих значений напряжения U(x) и тока I(x), а также активной мощности P(x);

в) по результатам расчетов построить совмещенные графики зависимостей для действующих значений U(x) и I(x), а также активной мощности P(x).

2.В переходном режиме при подключении линии без потерь (R0≈0;

G0≈0) к источнику постоянного напряжения 0 = √21| 1| рассчитать и построить совмещенные графики зависимостей распределения вдоль линии волн тока i(x, t0) и напряжения u(x, t0), соответствующих моменту времени

0 = 23 после подключения источника, когда отраженные от конца линии волны напряжения и тока достигли середины линии.

3.Проанализировать полученные результаты, графики зависимостей

исформулировать выводы по работе.

2

Рис. 1 Схема линии

Исходные данные:

Таблица 1

Рис. 2 Исходная схема

1.В установившемся режиме при заданном фазном напряжении

конце линии определяем следующие величины:

1.1.Волновое сопротивление:

= 475,1 1,9 Ом.

3

1.2.Постоянная распространения:

= √( 0 + 0) ( 0 + 0) =

=√(0,08 + 314 1,6 10−3) (0,5 10−6 + 314 0,7 10−8) =

=2,031 10−4 + 1,051 10−3 = +

где = 2,031 ∙ 10−4 1/км – коэффициент затухания;

β = 1,051 ∙ 10−3 рад/км = 0,06 град/км – коэффициент фазы.

1.3.Фазовая скорость:

1.6.Комплекс действующего значения тока в нагрузке:

1.7.Постоянные интегрирования:

=−2,142 104 + 1,78 105 = 1,79 105 96,862 , ;

1.8.Комплексы действующих значений напряжения и тока в начале линии при x = l = 1500 км:

4

̇1 = ̇1 + ̇2 −

= 3,227 105 86,195 (2,031 10−4+1,051 10−3) 1500 + +1,79 105 96,862 −(2,031 10−4+1,051 10−3) 1500 =

= −3,055 105 + 4,123 104 = 3,083 105 172,315 , ;

1̇= ̇1 − ̇2 − = −1195 + 63,115 = 1196 176,976 , A.

̇в ̇в

1.9.Активные мощности:

В конце линии

2 = 2 2 ( 2 − 2) = 500 103 316,37 ( 90 + 71,56 ) = 150,1 МВт;

В начале линии

1 = 1 1 ( 1 − 1) = 3,083 105 1196 ( 172,315 −

176,976 ) = 367,6 МВт.

1.10. Эффективность передачи энергии по линии:

1.11. Изменяя координату x от 0 до l = 1500 км по уравнениям

Рассчитываем с использованием программы Mathсad действующее значение напряжения ̇( ) и тока (̇), а также активную мощность ( ) =( ) ( ) ( − ). Результаты расчетов заносим в таблицу 2.

Таблица 2

5

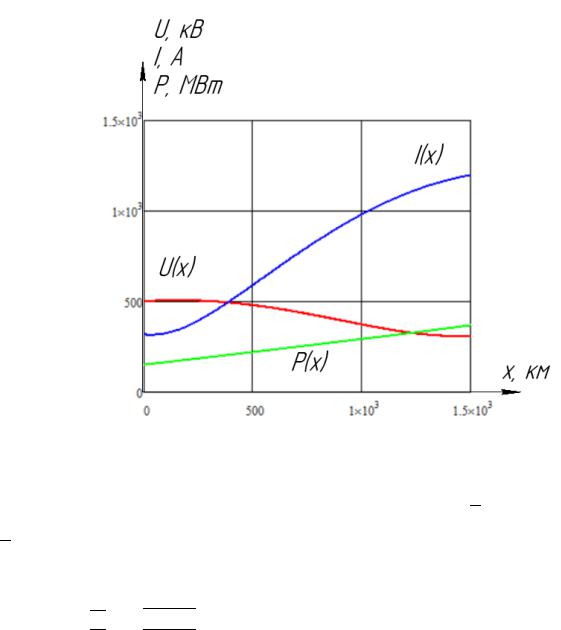
По данным таблицы строим совмещенные графики U(x), I(x) и P(x).

Рис. 3 Графики U(x), I(x) и P(x)

2. В переходном режиме для линии без потерь ( 0 ≈ 0, 0 ≈ 0), при подключении к источнику постоянного напряжения 0 = √2 1 ( 1) = √2 308,3 103 ( 172,315 ) = 58,3 кВ, определяем следующие величины:

2.1.Волновое сопротивление:

в = √ 0 = √1,6 10−3 = 478,09 Ом.

0 0,7 10−8

2.2.Фазовая скорость:

2.3.Падающие волны напряжения и тока:

методом (цепь первого порядка):

6

2.4.1. Определяем независимые начальные условия (ННУ) при = 0−

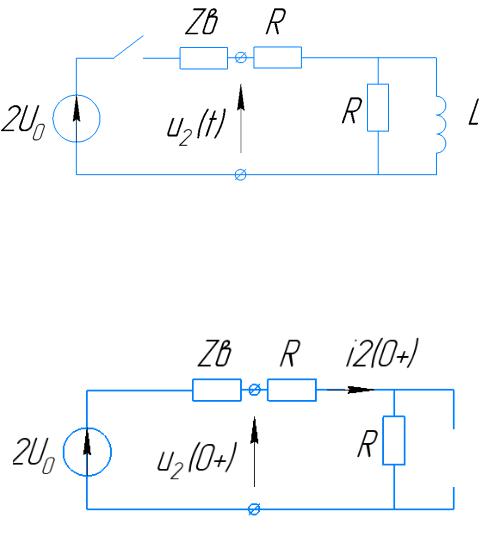
Рис. 4 Схема до коммутации

(0−) = 0

2.4.2. Зависимые начальные условия (ЗНУ) при t = 0+ (схема после коммутации ключа):

2(0+) = 2(0+) ( + ) = 47,056 (1000 + 1000) = 94,1 103 B. 2.4.3. Определяем принужденную составляющую при t = ∞: схема после

коммутации, установившийся режим, постоянный источник, C – разрыв, L –

закоротка.

7

Рис. 6 Схема после коммутации в установившемся режиме

2пр = 2пр = 78,89 1000 = 78,89 103 B.

2.4.4. Определяем корень характеристического уравнения p.

2.4.5.Постоянные интегрирования:

= 2(0+) − 2пр = 47,056 − 78,89 = −31,8 А;

= 2(0+) − 2пр = 94,1 103 − 78,89 103 = 15,22 103 В.

2.4.6.Окончательный результат:

2( ) = пр + = 78,9 − 31,8 −187,6 , ;2( ) = 2пр + = 78892 + 15220 −187,6 , .

2.5. Отраженные от конца линии волны напряжения:

отр( ) = 2( ) − пад = 15220 −187,6 + 20586 B;

отр = − отр( ) = −31,8 −187,6 − 43,1 A.

в

2.6.Рассчитываем распределение напряжения и тока вдоль линии для

источника, когда отраженные от конца линии волны напряжения и тока достигли середины линии.

Для этого заполняем таблицу 3.

8

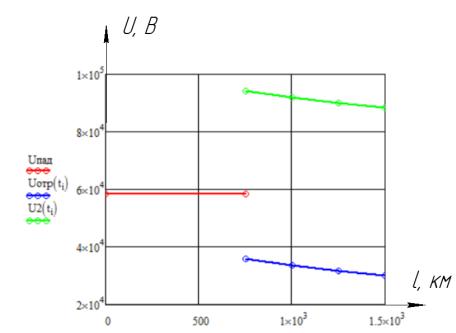
Таблица 3

Расчет ведется следующим образом:

2( Б) = 78892 + 15220 −187,6 8,367∙10−4 = 91,9 кВ.

Далее строим графики для t = t0.

Рис. 7 График зависимости напряжений от расстояния

9

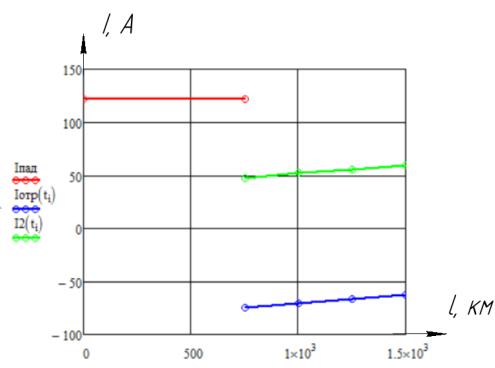
Рис. 8 График зависимости токов от расстояния

Вывод:

В данной работе был произведен расчет длинных линий в установившемся и переходном режимах.

Были найдены: волновое сопротивление, постоянная распространения,

фазовая скорость, длина волны, сопротивление нагрузки, комплексы действующих значений тока и напряжения, активная мощность и эффективность передачи энергии по линии.

В установившемся режиме по графику видно, что напряжение с увеличением х уменьшается, а ток и мощность возрастают.

Переходный процесс был рассчитан классическим методом для цепи первого порядка. Из графиков видно, что напряжения Uотр и U(x, t) падают, а

токи Iотр и I(x, t) увеличиваются.

10