1 семестр / Определённые интегралы. Кленина

Добавил:

PotapkinBY t.me Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Высшая математика

Файл:

интегрирования: при x = 0

следует, что t =cos0=1,

что t = cosp

что t = cosp

. Тогда интеграл I =òcos3 x×sin2xdx = -2òt4dt .

.pdf

Скачиваний:

Добавлен:

26.02.2023

Размер:

2.81 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

2.2. Табличное интегрирование


						3
Пример 2.2. Вычислить определенный интеграл x2dx
Решение. Воспользуемся	таблицей					2
Решение. Воспользуемся	таблицей				определенных
3	2dx	x3	3	1	27	8 19 .
3			3
(см. п риложение 4), получим x
(см. п риложение 4), получим x
2	3		2	3		3
2			2			b	x


Пример 2.3. Вычислить определенный интеграл								dx

							x
						a	x
						a

интегралов

, где a b .

Решение.

Рассмотрим

функцию

f x

Обозначим

x dx . Возможны следую щие случаи:

dx f

1. Если 0 a b , то x 0 (см. рис. 2.2), и

f x

Рис. 2.2. Случай 0 < a < b, тогда x > 0

Воспользуемся таблицей определенных интегралов, получим

b	b
I f x dx 1 dx x		ba b a .


a	a
2. Если a b 0, то x 0	(см. рис. 2.3), и f x		x	x	1.
			x

			x	x
			x	x

Рис. 2.3. Случай a ˂ b ˂ 0, тогда x ˂ 0

Воспользуемся таблицей определенных интегралов, получим


b	b
I f x dx 1 dx x		ba b a a b .


a	a

3.	Если a 0 b (см. рис. 2.4), тогда возможны положения пере-
менной	x x1	0 и x x2	0. Разбиваем интеграл на сумму двух инте-
	b	0	b
гралов:	I	f x dx f	x dx f x dx .
	a	a	0

Рис. 2.4. Случай a ˂ 0 ˂ b, тогда x = x1 ˂ 0 и x = x2 > 0

f x

x 1,

x dx

В первом интеграле x 0, и

тогда f

0a a . Учитываем, что a 0 .

dx x

Во втором интеграле

x 0, и

b0 b 0 b . Получили

f x

1, тогда

f x dx

1 dx x

I f x dx f x dx f

x dx b a .

Объединяя все три случая одной формулой,имеем

I f x

Пример 2.4. Вычислить определенный интеграл cosxdx .

Решение. Воспользуемся таблицей интегралов (см. приложен е 4)

2cosxdx sinx

0π2 sin

sin 0 1.

Пример 2.5. Вычислить определенный интеграл

1 x

Решение. Известна одна из первообразных функции

f x

–

1 x2

1arctg

это функция F x

. В самом деле,

вычислим производную

1 x2

F x , как производную сложной функции:

F x

arctg

1 x2

Упрощая выражение и раскрывая производную аргумента, имеем

1 x2 2

1 x2 x 2x

1 x2

1 2x2 x4 4x2 2

1 x2 2

f x .

1 x2

Получили

F x f x .

Следовательно,

действительно,

F x

1arctg

является первообразной функции f x . Применим фор-

мулу Ньютона-Лейбница для вычисления интеграла. Воспользуемся таблицей интегралов:

3	dx	F x		3	1	2x		3	1	arctg	3 arctg0	π

0
			0		2arctg		0		2				.
	1 x2					1 x2						6

Вывод: решение неверно, так как получили, что определенный интеграл от положительной функции является отрицательным числом.

Ошибка произошла из-за того, что первообразная F x				1arctg	2x	не
Ошибка произошла из-за того, что первообразная F x				1arctg	1 x2	не
				2	1 x2
является непрерывной функцией при	x 0;	3	. В точке	x 1 0;		3

функция F x имеет разрыв первого рода (скачок). Действительно, вычислим предел слева и справа функции F x при x 1. Получим:

lim

F x lim

1arctg

lim F x lim

1arctg

π .

1 x2

x 1 0

Таким образом,

lim

F x lim

F x .

x 1 0

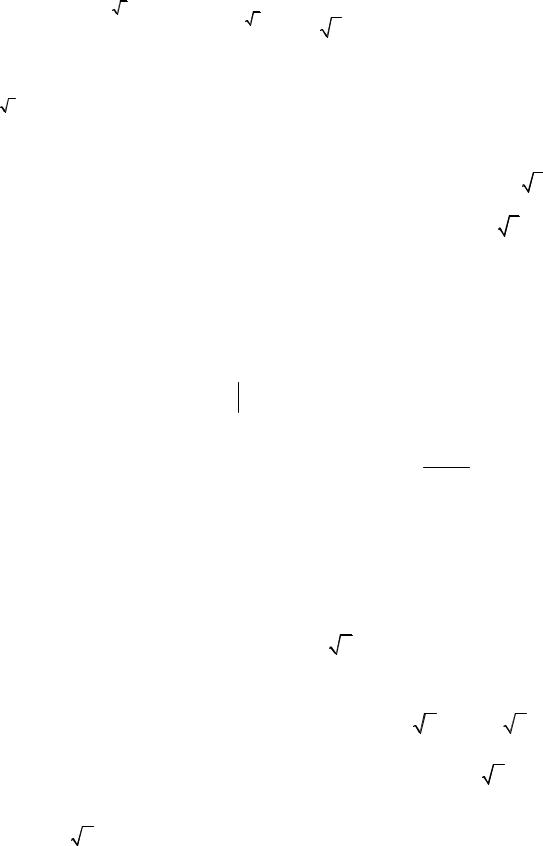
С другой стороны воспользуемся таблицей интегралов (см. приложение):

3 arctg

arctgx

3 arctg0

1 x

Здесь

формулу Ньютона-Лейбница

для вычисления

интеграла

первообразная F x arctgx

можно

применять, так как

функции

f x

является непрерывной функцией при

0; 3

и равенство F x

f x выполняется для всех точек отрезка 0;

3 .

Пример 2.6. Вычислить определенный интеграл exdx .

Решение: Воспользуемся таблицей определенных интегралов (см. приложение)

5 5

exdx ex 0 e5 e0 e5 1.

Пример 2.7. Вычислить определенный интеграл 2 dx 2 .

0 4 x

Решение: Воспользуемся таблицей интегралов

	2 dx			1		x	2		1	arctg1 arctg0			1	π				π
	2 dx			1		x	2		1				1	π				π
					arctg										0				.
	0 4 x2			2	arctg	2			2				2	4	0			8	.
							0				1
							0
												x 2 dx .
	Пример 2.8. Вычислить интеграл 1											x 2 dx .
											0
	Решение. Преобразуем подынтегральную функцию, используя
тождество квадрат суммы									двух		слагаемых		1			x 2	1 2 x x ,
																1			x 2 dx
и	разобьем		интеграл			на		сумму			трех	интегралов				1			x 2 dx
																0
1	1			1
1 dx 2		xdx xdx . Воспользуемся таблицей интегралов.
0	0			0

								1	10 1,											1
	Первый	интеграл: 1 dx x								второй			интеграл:							2	xdx
	Первый									второй			интеграл:								xdx

								0												0
1	1	2		3		1	4			1				1			1		1
1		2	x	3	2	1	4			1				1	x	2			1	. Объединяя
2 x2dx 2		3	x		2		3	и третий интеграл: xdx						2	x				2	. Объединяя
0						0				0			1				0				17 .
0						0				0							0
														1				x 2 dx
результаты вычисления трех интегралов, получим														1				x 2 dx
													0								6
													0
									π 4	1
	Пример 2.9. Вычислить интеграл									1		dx .
	Пример 2.9. Вычислить интеграл									2		dx .
									π 6	cos	x
									π 6

Решение. Воспользуемся таблицей интегралов

π 4	1			ππ	64
			dx tgx

	2	x
	2
π 6	cos
π 6

tg	π	tg	π	1	1	.
	4		6		3

			2 2					1
Пример 2.10. Вычислить интеграл						0			dx .
Пример 2.10. Вычислить интеграл						0		1 x2	dx .
Решение. Воспользуемся таблицей интегралов
2 2	1			022 arcsin			2					π				π
		dx arcsinx						arcsin0						0			.

	1 x2					2						4				4
0	1 x2					2						4				4
											π			1 cos22				x dx .
Пример 2.11. Вычислить определенный интеграл														1 cos22				x dx .
											0
Решение. Преобразуем подынтегральную функцию, используя три-
гонометрическое тождество 1 cos2x 2cos2 x . Тогда
													π
	1 cos2x						cosx, 0			x					,
			cos2 x				cosx, 0			x		2			,
					cosx					π					.
					cosx										.
	2
	2
							cosx,		2		x π
									2

			π
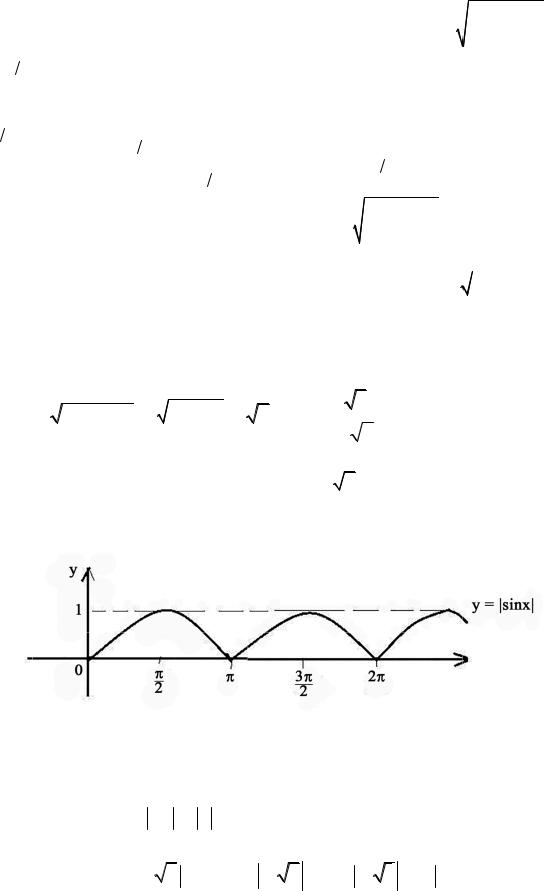
			π	1 cos22
	Разобьем	интеграл на	сумму двух интегралов	1 cos22	dx
			0
π 2	π	cos x dx .
	cosx dx	cos x dx .	Воспользуемся таблицей	интегралов:

0π2

π 2

cosx dx sinx

0π 2

cosx dx sinx

ππ

1. Объединяя резуль-

π 2

1 cos2x dx 2.

таты вычисления трех интегралов, получим

100π

Пример 2.12. Вычислить определенный интеграл

dx .

1 cos2x

Решение. Преобразуем подынтегральную функцию, используя три-

гоно метрическое тождество 1-cos2x =2 sin2 x . Тогда

2sinx,

0£ x £p,

1-cos2x =

2sin

x =

sinx

= ê

2sinx,

p< x £2p.

ê-

Подынтегральная

функция f (x)

= 2

sin x

является периодиче-

ской функцией (см. рис. 2.5) с периодом T = p.

Рис. 2.5. Изображение функции y = |sinx|

В самом деле, используя формулу приведения sin(x + π) = – sinx

и свойство модуля -a = a , получаем
f (x +p)= 2 sin(x +p) = 2 -sinx =	sinx = f (x).

Тогда отрезок интегрирования представим как [0,100p]=100×[0,p].

По свойству определенного интеграла его можно разбить на 100 отрезков с пределами интегрирования от 0 до p:

100p		100p			p
I = ò	1-cos2xdx =	2 ò	sinx	dx =100×	2ò	sinx	dx.

0		0			0

На отрезке [0,π] функция sinx ³0 – неотрицательна, следовательно, модуль можно отбросить: sinx =sinx для всех x Î [0,π].

Воспользуемся таблицей интегралов и формулой НьютонаЛейбница, получим

p			p		0p = -100 2(-1-1)= 200 2.
I =100 2ò	sinx	dx =100	2òsinxdx =100 2	(-cosx)


0			0

2.3. Применение метода замены переменных (подстановки)

Теорема. Пусть функция y = f (x) непрерывна на отрезке [a,b], а функция x = g(t) определена при t Î[α,β], имеет область значений отрезка [a,b], причем g(α) = a и g(β) = b.

Тогда, если функция x = g(t) имеет непрерывную производную g¢(t) при t Î[a,b], то справедлива формула замены переменной под зна-

b	b	(	)
ком определенного интеграла òf (x)dx =òf			g (t) g¢(t)dt .
a	a

Часто вместо замены переменной x = g(t) используют обратную замену переменной t = p(x).

Заметим, что при применении формулы замены переменной отпадает необходимость возвращения к старой переменной х по сравнению с неопределенным интегралом. Это вполне объяснимо, ибо определенный интеграл есть некоторое постоянное число, в то время как неопределенный интеграл от той же самой функции есть некоторая функция.

При замене переменной в определенном интеграле следует пом-

нить о том, что вводимая функция должна быть непрерывна на отрезке интегрирования. В противном случае формальное применение формулы приводит к абсурду. Рассмотрим пример.

Пример 2.13. Вычислить определенный интеграл òdx.

Решение. Используем табличное интегрирование:òdx = x

0p = p.

С другой стороны, если воспользоваться основным тригонометри-

ческим

тождеством

sin2 x +cos2 x =1,

то

получим,

что

òdx =ò

=ò

0 sin2 x +cos2 x

0 cos2 x×(1

+tg2x)

dt = d(tgx)=

Делаем

замену: t = tgx .

Находим

дифференциал

cos2 x

Меняем

пределы

интегрирования:

если

x = 0,

то t = tg0= 0;

если x = π, то t = tgπ = 0. Получимòdx =ò

= arctgt

00 =0 .

Таким образом, два способа нахождения интеграла дают различные результаты. Это произошло из-за того, что не был учтен тот факт, что введенная переменная t = tgx имеет на отрезке интегрирования раз-

рыв (в точкеx = p2Î[0,p]). Поэтому в данном случае такая подстановка

неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.

				7	dx
Пример 2.14. Вычислить определенный интегралò-1						.
					3x +4
Решение. Введем подстановку t = 3x +4 . Найдем дифференциал
dt = d( 3x +4)=			3dx	Выразим дифференциал dx через dt.
		2	3x +4
Тогда	dx		= 2dt	– подынтегральное выражение. Найдем новые
	3x +4
			3

пределы интегрирования: при x =-1 следует t = -3								+4 =1, при x = 7
следует t = 3 7+4 = 25 =5. Тогда интеграл
7	dx	5		5

ò		=ò2dt =	2t	=	2×5	-1=	8 .

-1	3x +4	1 3	3	1	3		3

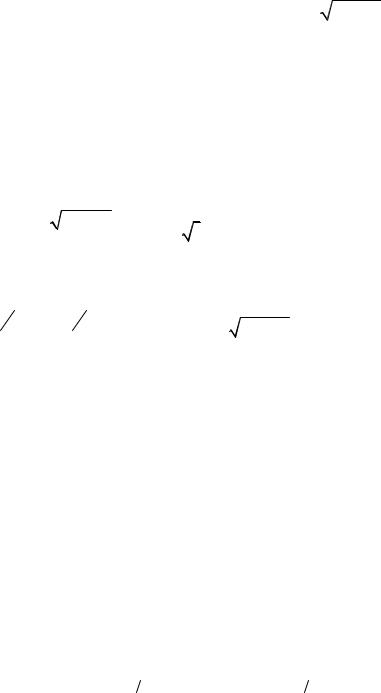
2	1+lnx
Пример 2.15. Вычислить определенный интеграл I =ò		dx .

1	x

Решение. Введем подстановку t =1+lnx . Найдем дифференциал dt = d(1+lnx)= dxx . Видим, что под знаком интеграла находится диффе-

ренциал новой переменной: dxx = dt . Найдем новые пределы интегрирования: при x =1 следует t =1+ln1=1, при x = 2 следует t =1+ln2.

2	1+lnx		1+ln2
Тогда интеграл I =ò		dx =	ò	tdt . Воспользуемся таблицей

1	x		1

интегралов (см. приложение4) и формулой Ньютона-Лейбница. Получим

1+ln2	1		2	3		1+ln2	2	((1+ln2) 1+ln2	-1).
1+ln2	1		2	3		1+ln2	2
I = ò t		2dx =	3t		2	=	3
1						1
1						1

Пример2.16. Вычислитьопределенныйинтеграл I =òcos3 x×sin2xdx .

Решение. Преобразуем подынтегральную функцию f (x)= cos3 x sin2x , заменяя sin2x по формуле синуса двойного аргу-

мента sin2x =2sinx cosx , а именно: f (x)= cos3 x×(2sinxcosx)=

= 2cos4 x×sinx .
Введем замену.	Обозначим t = cosx . Найдем дифференциал
dt = d(cosx)= -sinxdx	Заметим, что под знаком интеграла находится

дифференциал новой переменной: sinxdx = -dt . Найдем новые пределы

Меняем порядок интегрирования I = 2òt4dx .

Воспользуемся таблицей интегралов (см. приложение) и формулой Ньютона-Лейбница. Получим

	2			1		2	æ	1	ö		31

I =		t	5		=		ç1-		÷	=		.
									÷
	5					5	ç	32	÷		80
				1/2			è		ø

Пример 2.17. Вычислить определенный интеграл I = ln3 dx .

òln2 ex +e-x

Решение. Введем замену. Обозначим t = ex . Найдем дифференциал dt = d(ex )= ex ×dt Выразим дифференциал dx через dt. Тогда dx = edxt = dtt

. Заметим, что e-x = e1x =1t . Преобразуем подынтегральное выражение

. Найдем

новые

пределы интегрирования: при

ex +e-x

t +

t2 +1

x =ln2

следует t =eln2 =2, при x =ln3 следует t =eln3 =3. Тогда ин-

теграл

ln3

I =ò

=ò

x -x

ln2 e

2 t

Воспользуемся таблицей интегралов (см. приложение 4) и формулой Ньютона-Лейбница. Получим I =arctgx 32 =arctg3-arctg2.

p 2

Пример 2.18. Вычислить определенный интеграл I =ò

2+сosx

Решение. Заменяя переменную при помощи универсальной триго-

нометрической подстановки t = tg

, получим

= arctgt

или

x = 2arctgt .

Найдем дифференциал dx = 2d(arctgt)=

2dt

. Выразим cosx через

1+t2

t . Запишем тригонометрическое тождество 1+tg

. Отсюда

cos

cos2 2x =1+1t2 . Преобразуем cosx по формуле половинного аргумента

cosx =2cos2 2x -1 и выразим правую часть последнего тождества через t с учетом замены: cosx =2cos2 2x -1=1+2t2 -1=11+-tt22 .

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

Соседние файлы в папке 1 семестр

#
26.02.2023729.38 Кб71 семестр. Лекции. Кленина.pdf
#
26.02.20238.08 Mб5Мои шпоры.docx
#
26.02.20232.6 Mб7Мои шпоры.pdf
#
26.02.20232.81 Mб7Определённые интегралы. Кленина.pdf
#
26.02.20236.61 Mб2Практика из ЭП (1).jpg
#
26.02.20236.94 Mб2Практика из ЭП (10).jpg
#
26.02.20235.49 Mб3Практика из ЭП (11).jpg
#
26.02.20236.5 Mб3Практика из ЭП (2).jpg
#
26.02.20236.31 Mб2Практика из ЭП (3).jpg