
Предел суммы, произведения и частного

Переход к пределу в неравенствах, предел промежуточной функции
Теорема
(о переходе к пределу в неравенствах):
Пусть существуют конечные пределы в
некоторой окрестности т.

 ,
,
 .
Тогда: если
.
Тогда: если
 ,
то
,
то
 .
.
Доказательство.
 ,
,
 ,
тогда:
,
тогда:
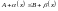 ,
,

Теорема
(о пределе промежуточной функции):
Если
 в некоторой окрестности т.
и
в некоторой окрестности т.
и
 ,
то
,
то
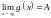 .
.
Доказательство.
Пусть
 ,
тогда по теореме о переходе к пределу
в неравенствах:
,
тогда по теореме о переходе к пределу
в неравенствах:
 ,
,

 ,
,
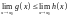 ,
,
 ,
,
Следовательно,
 и
.
и
.
Непрерывность функции в точке
Функция
 называется непрерывной
в т.
,
если
называется непрерывной
в т.
,
если
 .
.
Замечание: элементарные функции непрерывны в точках, где определены.
Теорема
(о переходе к пределу, под знаком
непрерывности):
Если функция
непрерывна в т.
,
то
 .
.
Доказательство.
Т.к.
 и функция непрерывна, т.е.
.
Следовательно
.
и функция непрерывна, т.е.
.
Следовательно
.
Непрерывность основных элементарных функций
Теорема
(о непрерывности сложной функции):
Пусть
непрерывна в т.
,
а функция
 непрерывна в т.
непрерывна в т.
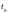 .
Тогда сложная функция
.
Тогда сложная функция
 непрерывна в точке
непрерывна в точке
Доказательство.

Теорема:
Пусть
и
 непрерывны в т.
,
тогда
непрерывны в т.
,
тогда
 ,
,
 ,
,
 (
( )
тоже непрерывны в этой точке.
)
тоже непрерывны в этой точке.
Доказательство:
основано на свойствах предела. Т.к.
функция непрерывна, то
 .
.
Теорема об асимптотическом разложении непрерывной функции
Теорема
(асимптотическое разложение непрерывной
функции):
Если функция
непрерывна в т.
,
то в некоторой окрестности этой т.,
функция
представима в виде:
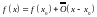 .
.
Доказательство.
Рассмотрим
 .
По теореме об асимптотическом разложении
функции имеющей предел:
.
По теореме об асимптотическом разложении
функции имеющей предел:
 .
Т.к. функция непрерывна, то
,
т.е.
.
.
Т.к. функция непрерывна, то
,
т.е.
.
Свойства функций, непрерывных на отрезке
Свойства
(для интервалов
 ,
,
 и
и
 ):
):
1)
Если функция
 непрерывна в точке
,
то в некоторой окрестности этой точки
знак
совпадает со знаком
непрерывна в точке
,
то в некоторой окрестности этой точки
знак
совпадает со знаком
 .
.
2)
Если функция
непрерывна на интервале
и
 ,
то существует хотя бы одна точка
,
то существует хотя бы одна точка
 ,
т.ч.
,
т.ч.
 .
.
3)
Если функция
непрерывна на интервале
,
то она достигает на этом интервале
наибольшее и наименьшее значения, т.е.
 ,
т.ч.
,
т.ч.
 и
и

 .
.
4) Если функция непрерывна на интервале , то она ограничена.
Теоремы о переходе к пределу под знаком непрерывной функции, о непрерывности сложной функции.
Теорема (о переходе к пределу, под знаком непрерывности): Если функция непрерывна в т. , то .
Доказательство. Т.к. и функция непрерывна, т.е. . Следовательно .
Теорема (о непрерывности сложной функции): Пусть непрерывна в т. , а функция непрерывна в т. . Тогда сложная функция непрерывна в точке
Доказательство.
Односторонние пределы
 :
Число
:
Число
 называется односторонним пределом
слева, если
называется односторонним пределом
слева, если
 ,
,
 ,
т.ч.
,
т.ч.
 ,
,
 :
:

 :
Число
:
Число
 называется односторонним пределом
справа, если
,
,
т.ч.
,
называется односторонним пределом
справа, если
,
,
т.ч.
,
 :
:
Теорема:
Для того, чтобы
имела в т.
предел, необходимо и достаточно чтобы
существовали односторонние пределы:
 .
.
Функция называется непрерывной в т. , если .
Замечание: элементарные функции непрерывны в точках, где определены.
Точки разрыва функции, их классификация
Точка
,
называется точкой разрыва первого рода
если: 1)
 2) Существуют конечные односторонние
пределы, но они не совпадают, т.е. не
существует предела.
2) Существуют конечные односторонние
пределы, но они не совпадают, т.е. не
существует предела.
Точка , называется точкой разрыва второго рода если хотя бы один из односторонних пределов не существует или равен бесконечности.
Замечательные пределы

Эквивалентные бесконечно малые функции
Функция
 называется бесконечно малой, если
называется бесконечно малой, если
 ,
т.е.
,
,
т.ч.
,
,
т.е.
,
,
т.ч.
,
 :
:
 .
.
Функции
и
 называются эквивалентными б/м при
называются эквивалентными б/м при
 ,
если
,
если
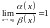 и обозначаются
и обозначаются
 .
.
Теорема:
Для того, чтобы
,
необходимо и достаточно, чтобы
 была б/м более высокого порядка чем
и
.
была б/м более высокого порядка чем
и
.
Таблица эквивалентных бесконечно малых
 ,
,
 ,
,
 ,
,
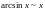 ,
,
 ,
,
 ,
,
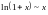 ,
,
 ,
,
 .
.
Теорема о замене бесконечно малых эквивалентными при вычислении пределов
Теорема
(о замене б/м на эквивалентные в
отношениях):
Пусть ,
,
 эквивалентные б/м при
.
Тогда
эквивалентные б/м при
.
Тогда
 .
.
Доказательство.
Рассмотрим
 .
Тогда,
.
Тогда,
 .
.
Производная, её геометрический и механический смысл
Геометрический смысл производной состоит в том, что значение производной функции y=f(x) в точке хо равно угловому коэффициенту касательной к графику функции в точке с абсциссой Хо: f'(x0) = k = tga

Уравнение касательной и нормали к графику функции

Дифференцируемость функции, дифференциал
Функция f(x) называется дифференцируемой в точке х0, если её приращение в этой точке может быть представлено в виде
дельта f(x0)= f(x0 + дельта x) - f(x0) = A*дельта x+ о(дельта x), где А - некоторое число; о(дельта х) - бесконечно малая функция более высокого порядка малости, чем дельта х при х -> 0.
Дифференциал
функции y
= f(x)
равен произведению её производной на
приращение независимой переменной x (аргумента).
![]()
Необходимое и достаточное условие дифференцируемости


Геометрический смысл дифференциала

Дифференциал функции двух переменных равен приращению аргумента аппликаты касательной плоскости.
Приближенные вычисления с помощью дифференциала

Непрерывность дифференцируемой функции
Теорема. Если функция y = f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.
Таким образом, из дифференцируемости функции следует ее непрерывность.
Доказательство.
Если  ,
то
,
то

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда Δy=f '(x0) Δx+αΔx=> Δy→0 при Δx→0, т.е f(x) – f(x0)→0 при x→x0, а это и означает, что функция f(x) непрерывна в точке x0. Что и требовалось доказать.
Производная суммы, произведения и частного




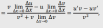
Производная сложной функции

Производная обратной функции
I.
Если
 (D
– область определения) поставлен в
соответствие
(D
– область определения) поставлен в
соответствие
 ,
говорят, задана функция
.
Если это взаимно однозначно, то можно
рассмотреть функцию
,
говорят, задана функция
.
Если это взаимно однозначно, то можно
рассмотреть функцию
 ,
которая
,
которая
 ставит в соответствие x.
ставит в соответствие x.
Теорема:
Пусть
 и
взаимно обратные функции, тогда
и
взаимно обратные функции, тогда
 или
или
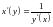 .
Доказательство. Пусть обе функции
дифференцируемы в некоторой точке.
Тогда,
.
Доказательство. Пусть обе функции
дифференцируемы в некоторой точке.
Тогда,
 , т.к. обе функции дифференцируемы
непрерывны, т.е.
, т.к. обе функции дифференцируемы
непрерывны, т.е.
 при
при
 .
Тогда,
.
Тогда,

Производные обратных тригонометрических функций
а)
 ,
,
 ,
тогда
,
тогда
 ,
,
б)
 ,
,
 ,
,
 ,
,
в)
 ,
,
 ,
,
 ,
,
г)
 ,
,
 ,
,
 .
.
Параметрическое задание функции
Пара уравнений x = x(t) и y= y(t) где t- вспомогательная переменная, задаёт некоторую линию. Этот способ задания линии называется параметрическим, а переменная t-параметром. Исключая t получаем обычное уравнение той же линии: y= y (g(x))
Производные первого и второго порядка функций, заданных параметрически
I.
Производной 2-го порядка от функции
называется производная от ее первой
производной:
 .
Вообще, производной n-го
порядка называется производная от
производной порядка n-1:
.
Вообще, производной n-го
порядка называется производная от
производной порядка n-1:
 .
.
II.
Пусть функция
дифференцируема, тогда приращение
функции
 ,
следовательно
,
следовательно
 - дифференциал I-го
порядка.
- дифференциал I-го
порядка.
Рассмотрим
1-й
случай, когда x
– независимая переменная. Тогда
 - число. Предполагая, что функция
дифференцируема дважды в т. x,
найдем дифференциал от дифференциала
I-го
порядка при
- число. Предполагая, что функция
дифференцируема дважды в т. x,
найдем дифференциал от дифференциала
I-го
порядка при
 :
:
 ,
,
 - полученное выражение при
называется дифференциалом II-го
порядка. Аналогично:
- полученное выражение при
называется дифференциалом II-го
порядка. Аналогично:
 ,
,
 .
.
Рассмотрим
2-й
случай, когда
 ,
а
,
а
 - соответственно сложная функция. Тогда
- дифференциал I-го
порядка, а
- функция,
- соответственно сложная функция. Тогда
- дифференциал I-го
порядка, а
- функция,
 .
Тогда:
.
Тогда:
 ,
,
 ,
,
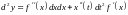 ,
,
 .
Дифференциалы 2-го (и более высокого
порядка) не обладают инвариантностью
формы (т.е. меняют вид в зависимости от
x).
.
Дифференциалы 2-го (и более высокого
порядка) не обладают инвариантностью
формы (т.е. меняют вид в зависимости от
x).
Касательная к кривой, заданной параметрически

Производные и дифференциалы высших порядков
I.
Производной 2-го порядка от функции
называется производная от ее первой
производной:
 .
Вообще, производной n-го
порядка называется производная от
производной порядка n-1:
.
Вообще, производной n-го
порядка называется производная от
производной порядка n-1:
 .
.
II.
Пусть функция
дифференцируема, тогда приращение
функции
 ,
следовательно
- дифференциал I-го
порядка.
,
следовательно
- дифференциал I-го
порядка.
Рассмотрим
1-й
случай, когда x
– независимая переменная. Тогда
- число. Предполагая, что функция
дифференцируема дважды в т. x,
найдем дифференциал от дифференциала
I-го
порядка при
:
 ,
,
 - полученное выражение при
называется дифференциалом II-го
порядка. Аналогично:
,
.
- полученное выражение при
называется дифференциалом II-го
порядка. Аналогично:
,
.
Рассмотрим
2-й
случай, когда
,
а
- соответственно сложная функция. Тогда
- дифференциал I-го
порядка, а
- функция,
.
Тогда:
,
,
 ,
,
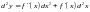 .
Дифференциалы 2-го (и более высокого
порядка) не обладают инвариантностью
формы (т.е. меняют вид в зависимости от
x).
.
Дифференциалы 2-го (и более высокого
порядка) не обладают инвариантностью
формы (т.е. меняют вид в зависимости от
x).
Формула Лейбница

Формула
Лейбница для n-ой производной произведения
двух функций — обобщение правила
дифференцирования произведения (и
отношения) двух функций на случай
n-кратного дифференцирования. Пусть
f(z) и g(z) - n раз дифференцируемые функции,
тогда
![]()
Основные теоремы дифференциального исчисления (Ролля, Лагранжа, Коши) и их геометрический смысл
Теорема
Ролля:
Пусть функция
непрерывна на отрезке
,
дифференцируема хотя бы на отрезке
и значение функции на концах отрезка
совпадает, т.е.
 ,
тогда существует хотя бы одна точка
,
тогда существует хотя бы одна точка
 ,
т.ч.
,
т.ч.
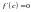 .
.
Доказательство.
1) Пусть наибольшее и наименьшее значения
функции
на отрезке
совпадают, т.е.
 и функция
постоянна тогда
и функция
постоянна тогда
 производная
.
2) Пусть функция непостоянна, тогда она
достигает на интервале
наибольшего и наименьшего значения.
Причем функция не может достигать
производная
.
2) Пусть функция непостоянна, тогда она
достигает на интервале
наибольшего и наименьшего значения.
Причем функция не может достигать
 и
и
 на концах отрезка, т.к.
на концах отрезка, т.к.
 и функция была бы постоянна. Значит,
внутри интервала
и функция была бы постоянна. Значит,
внутри интервала
 есть точка экстремума
есть точка экстремума
 ,
,

Геометрический
смысл.
Если все условия теоремы выполнены, то
на графике функции
существует точка
 ,
через которую проходит касательная к
графику функции, параллельно оси x.
,
через которую проходит касательная к
графику функции, параллельно оси x.
Теорема
Лагранжа:
Пусть функция
непрерывна на отрезке
,
дифференцируема хотя бы на отрезке
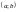 ,
тогда существует точка
,
тогда существует точка
 ,
т.ч.
,
т.ч.
 .
.
Доказательство.
Рассмотрим вспомогательную функцию
 непрерывную на отрезке
,
дифференцируемую хотя бы на отрезке
:
непрерывную на отрезке
,
дифференцируемую хотя бы на отрезке
:
 .
Тогда
.
Тогда
 ,
а
,
а
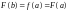 ,
т.е. выполнены все условия теоремы Ролля
и существует
,
т.ч.
,
т.е. выполнены все условия теоремы Ролля
и существует
,
т.ч.
 .
Следовательно,
.
Следовательно,
 ,
,
 .
.
Из
теоремы Лагранжа следует формула
конечных приращений:
 .
.
Геометрический
смысл.
 -
-
 угла наклона секущей (хорды), стягивающей
точки
угла наклона секущей (хорды), стягивающей
точки
 и
и
 графика
.
графика
.
 -
угла наклона касательной к графику
функции
,
через точку касания
.
Если все условия теоремы Лагранжа
выполнены, то касательная проходящая
через точку
-
угла наклона касательной к графику
функции
,
через точку касания
.
Если все условия теоремы Лагранжа
выполнены, то касательная проходящая
через точку
 ,
параллельна секущей (хорде), точки
,
параллельна секущей (хорде), точки
 и
и
 графика
графика
 .
.
Теорема
Коши:
Пусть функция
и
непрерывны
на отрезке
,
дифференцируемы хотя бы на отрезке
 ,
,
 ,
тогда существует точка
,
т.ч.
,
тогда существует точка
,
т.ч.
 .
.
Доказательство.
Рассмотрим вспомогательную функцию
непрерывную на отрезке
,
дифференцируемую хотя бы на отрезке
:
 .
Тогда
.
Тогда
 ,
,
 ,
т.е. выполнены все условия теоремы Ролля
и существует
,
т.ч.
.
Следовательно,
,
т.е. выполнены все условия теоремы Ролля
и существует
,
т.ч.
.
Следовательно,
 ,
,
 .
.
Правило Лопиталя для вычисления пределов
Теорема:
Пусть
и
б/м ( )
определенные и дифференцируемые в
окрестности т.
,
за исключением может быть самой т.
, причем
и
)
определенные и дифференцируемые в
окрестности т.
,
за исключением может быть самой т.
, причем
и
 ,
существует
,
существует
 .
Тогда
.
Тогда
 .
.
Доказательство.
Пусть
 - конечное число. Доопределим функции
и
,
предполагая, что
- конечное число. Доопределим функции
и
,
предполагая, что
 .
Тогда эти функции непрерывны в точке
.
Рассмотрим интервал
.
Тогда эти функции непрерывны в точке
.
Рассмотрим интервал
 ,
где
,
где
 .
Тогда
и
непрерывны на отрезке
и дифференцируемы на интервале
.
Тогда
и
непрерывны на отрезке
и дифференцируемы на интервале
 .
Тогда по теореме Коши
.
Тогда по теореме Коши
 ,
т.ч.
,
т.ч.
 ,
или
,
или
 .
Т.к.
.
Т.к.
 ,
то и
,
то и
 .
Следовательно получим:
.
Следовательно получим:
 .
.
Теорема:
Пусть
и
б/б ( )
определенные и дифференцируемые в
окрестности т.
,
причем
и
)
определенные и дифференцируемые в
окрестности т.
,
причем
и
 ,
существует
,
существует
 .
Тогда
.
Тогда
 .
.
Т.е.
правило Лопиталя годится не только для
неопред. вида
 ,
но и для
,
но и для
 .
.
Условие возрастания и убывания дифференцируемой функции на интервале
Функция
на интервале
,
при
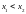 ,
где
,
где
 ,
называется возрастающей,
если
,
называется возрастающей,
если
 и убывающей,
если
и убывающей,
если
 .
.
Пусть
функция
дифференцируема на интервале
при всех
 тогда: если
тогда: если
 ,
то функция возрастает
на
,
а если
,
то функция возрастает
на
,
а если
 ,
то функция убывает
на
этом интервале.
,
то функция убывает
на
этом интервале.
Если
существует окрестность точки
,
такая что для всех точек
 ,
принадлежащих этой окрестности,
выполняется неравенство
,
принадлежащих этой окрестности,
выполняется неравенство
 (или
(или
 ),
то
- называется точкой
минимума
(максимума) этой функции, а
- локальным
минимумом
(максимумом) этой функции.
),
то
- называется точкой
минимума
(максимума) этой функции, а
- локальным
минимумом
(максимумом) этой функции.
Точки максимума и минимума функции называются точками локального экстремума.
Теорема
(необходимое условие экстремума):
Если
имеет в точке экстремума
производную
 ,
то
,
то
 .
.
Замечание. В точке экстремума:
1)
может не существовать производной.
Пример:
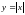 ,
,
 -минимум, а
не существует.
-минимум, а
не существует.
2)
 .
Пример:
.
Пример:
 ,
-минимум, но
,
-минимум, но
Вывод: если в т. экстремум, то , , не существует.
Теорема (достаточное условие экстремума): Пусть функция дифференцируема в некоторой окрестности точки , может быть за исключением самой точки . Тогда, если при переходе через точку , меняет знак с "+" на "–", то в точке - максимум, а если с "–" на "+" – минимум. Если же не меняет свой знак при переходе через точку , то она не является точкой экстремума.
Экстремумы функции
Определение 1. Точка х0 называется точкой максимума функции f(x), если в некоторой окрестности точки х0 выполняется неравенство f(x) <=f(x0)
Определение 2. Точка х1 называется точкой минимума функции f(x), если в некоторой окрестности точки х1 выполняется неравенство f(x) >=f(x1)
Необходимые условия экстремума
Теорема (необходимое условие экстремума): Если имеет в точке экстремума производную , то .
Замечание. В точке экстремума:
1)
может не существовать производной.
Пример:
 ,
,
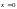 -минимум, а
-минимум, а
 не существует.
не существует.
2)
 .
Пример:
.
Пример:
 ,
-минимум, но
,
-минимум, но
