
новая папка 1 / 303197
.pdf
1737
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра физики и биомедицинской техники
ИССЛЕДОВАНИЕ РАСПРЕДЕЛЕНИЯ СРЕДНЕГО ЧИСЛА ВЫБРОСОВ УЗКОПОЛОСНЫХ ПРОЦЕССОВ НА ПРИМЕРЕ ГАУССОВА ШУМА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторной работе № 3
по курсу «Автоматизация обработки экспериментальных данных»
Липецк Липецкий государственный технический университет
2013
УДК 537.1
Составители В.Ф. Осинин, Д.А.Подлесных, С.И. Шарапов, А.А.Демидова, С.Ф. Четвериков Рецензент - доктор технических наук, профессор В.Н.Малыш
И 889 Исследование распределения среднего числа выбросов узкополосных процессов на примере гауссова шума [Текст]: методические указания к лабораторной работе № 3 по курсу «Автоматизация обработки экспериментальных данных» / сост.: В.Ф. Осинин, [и др.] – Липецк: Изд-во ЛГТУ, 2013. – 13 с.
Методические указания предназначены для студентов 3,4 -го курсов специальности 20040.65 «Инженерное дело в медико-биологической практике» и направления 201000.62 «Биотехнические системы и технологии» по дисциплине «Автоматизация обработки экспериментальных данных ».
Табл. 2 . Ил. 7. Библиогр.: 5 назв.
© Липецкий государственный технический университет, 2013

ЛАБОРАТОРНАЯ РАБОТА № 3
ИССЛЕДОВАНИЕ РАСПРЕДЕЛЕНИЯ СРЕДНЕГО ЧИСЛА ВЫБРОСОВ УЗКОПОЛОСНЫХ ПРОЦЕССОВ НА ПРИМЕРЕ ГАУССОВА ШУМА
Цель работы
1.Получить распределение среднего числа выбросов для нормального шума.
2.Проверить работу пороговых каналов анализатора в режиме измерения среднего числа выбросов.
3.Определить эффективную полосу пропускания узкополосного приемника.
Блок-схема аппаратурного комплекса
Для приема, накопления и обработки сигналов используется аппаратурный комплекс, изображенный на рис. 1.
Рис. 1. Блок-схема аппаратурного комплекса
Напряжение нормального шума с заданными параметрами поступает с генератора через антенный усилитель и приемник на статистический анализатор, который позволяет получить статистические характеристики радиошума в полосе f на частоте приема f.
Это позволяет в дальнейшем провести калибровку опорных уровней ста-
тистического анализатора в абсолютных единицах, исходя из известных пара-
метров системы.
3
Краткая теория
Процессы, протекающие в живом организме, носят в основном периодический характер. В то же время сигналы, несущие информацию о состоянии биологических объектов, содержат случайную составляющую,
возникающую как результат внешних воздействий на объект и помех в регистрирующих устройствах.
Для обработки таких сигналов и выделения информативной составляющей необходимо использовать методы обработки экспери-
ментальных данных, в частности алгоритмы оценки законов распределения среднего числа выбросов узкополосных процессов.
Число превышений некоторого порогового уровня случайным
процессом
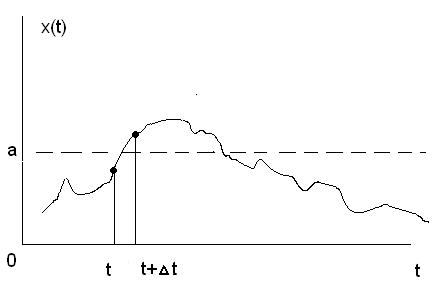
Будем считать, что стационарный случайный процесс задан своим законом распределения и корреляционной функцией. Зафиксируем уровень a (рис.2) и будем искать вероятностные характеристики выбросов над уровнем
а. Найдем, прежде всего, вероятность Р(х>а, t), т.е. вероятность того, что за малый интервал времени [t, t+ t] будет иметь место одно пересечение уровня а снизу вверх.
Рис. 2. График случайного процесса
4
Очевидно, для этого должны быть одновременно выполнены два условия x(t)<a и x(t + t)>a.
Считая данный случайный процесс процессом с непрерывной производной, можно написать, что
|
x( t t ) x( t ) |
|
dx |
y( t ), |
(1) |
|
|
t |
|
dt |
|||
|
|
|
|
|||
откуда х(t + t) x(t)+y(t) t. |
|
|
|
|
||
С учетом этого можно написать x(t + t)- y(t) t x(t) <a, но x(t + t) > a;
х(t + t)-а >0. Или а - х(t + t) + x(t) <х(t)<а, то а- y(t) t < x(t)< а.
Найдём вероятность выполнения этого условия, считая, что двумерный
закон W2(х,у), т.е. закон распределения x(t) и её производной |
y t |
dx( t ) |
, |
||
dt |
|||||
|
|
|
|
||
известен. Очевидно, что |
|
|
|
|
|
P x a, t |
W2 x,y dx,dy |
(2) |
|||
|
a y t t x t a,y 0 |
|
|
|
|
Так как речь идет о превышении уровня a, то интегрирование по производной у должно вестись с соблюдением у>0. Принимая это во внимание, перепишем
|
P x a, t |
dy |
|
W2 x, y dx . |
|
|
|
0 y |
a y t t x t a |
|
|
Применим теорему о среднем в интегральном исчислении |
|
||||
|
f x dx b a f x* , |
где а<x <b, и перепишем интеграл по x в |
|||
|
b x* a |
|
|
|
|
виде |
W2 x, y dx a a y t W2 x*, y W2 x*, y y t t . |
|
|||
|
a y t t x t a |
|
|
|
|
|
Если t мало, то х* слабо отличается от а и можно х* заменить на а, т.е |
||||
|
P x a, t t |
yW2 a, y dy t J a |
(3) |
||
|
|
0 y |
|
|
|
5
Величину J a |
yW2 a, y dy можно рассматривать как |
|
0 y |
среднюю скорость процесса при его значении, равном а. Таким образом,
искомая вероятность пропорциональна интервалу t и средней скорости процесса при его значении, равном уровню а.
Теперь найдем среднее число выбросов за время Т . Так как за время t
может быть только один выброс с вероятностью р(х>а, t), то за время Т
будет Nа,T выбросов, где |
|
|
|
|
T |
P x a, t , т.е. |
|
||
Na,T |
|
||||||||
t |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a,T T |
yW2 a, y dy T J a |
(4) |
|||||
N |
|||||||||
|
|
0 y |
|
|
|
|
|||
Отсюда видно, что J(а) представляет собой среднюю частоту выбросов, или среднее число выбросов в секунду:
J(a)= Nа, T / Т. (5)
Для нормального случайного стационарного процесса x(t) с
производной по времени y(t) = dx/dt, средним значением m1х, дисперсиями σх и σу среднее число выбросов определяется как
|
|
y |
|
|
2 |
|
|
J a |
|
|
|
a m1x |
|
|
|
|
|
|
exp |
|
|
(6) |
|
2 |
|
2 2 |
|||||
|
x |
|
. |
||||
|
|
|
|
x |
|
|
|
Определение распределения среднего числа выбросов огибающей
напряжения узкополосного случайного процесса на примере нормального
шума
Гауссовский процесс, сформированный из белого нормального шума вырезанием относительно узкой полосы частот, представляет собой случайный
процесс по виду схожий с гармоническим колебанием |
|
t |
|
|
|
x t A t cos 0t t . A t cos t |
(7) |
где A(t) – огибающая;
- медленно меняющиеся функции времени t;
θ(t) – фаза,
6

ω0 – циклическая частота.
Рассмотрим стационарный эргодический процесс с нормальным законом распределения вероятности (рис. 3).
 P
P
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
Рис. 3. График стационарного эргодического процесса |
|
|||||||||
|
|
1 |
|
|
x x |
2 |
|
, |
(8) |
|
p( x ) |
|
|
exp |
|
|
|||||
|
|
|
2 2 |
|
||||||
2 |
|
|||||||||
|
|
|
|
|
|
|
||||
где и x его дисперсия и среднее значение соответственно.
Рассмотрим свойства распределения среднего числа выбросов огибающей узкополосного нормально - флуктуационного напряжения с нулевым
средним, т.е. х 0 . Для него аналитическое выражение известно
|
V |
|
|
V 2 |
|
|
|||||
N (V V0 ) |
|
|
|
|
|
|
|
|
|
|
(9) |
|
|
|
|
|
|
2 |
|||||
|
2 |
exp |
2 |
|
|||||||
|
|
|
|
|
|
|
|||||
где N(V>V0) – среднее число превышений в единицу времени порога V0 узкополосным флуктуирующим напряжением V;
V – напряжение огибающей узкополосного гауссова шума;
V0 – пороговое напряжение на входе некоторого канала анализатора;– эффективное напряжение шума на выходе генератора;
– среднеквадратичная полоса спектра флуктуаций шума приемника.
Легко видеть, что максимум функции существует при V = и зависит только от среднеквадратичной полосы спектра флюктуации
N (V ) |
|
N |
|
(V V ) |
|
|
e |
1 |
2 f |
|
e |
1 |
2 |
, |
(10) |
|
приV |
m ax |
|
|
|
|
э |
|
|||||||||
|
|
0 |
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где – среднеквадратичная полоса спектра флюктуации, связанная с эквивалентной энергетической полосой пропускания узкополосного приемника
7
формулой = |
|
|
|
|
|
|
|||
2 fэ ; |
fэ – эквивалентная энергетическая |
полоса пропуска- |
|||||||
ния приемника, определяемая выражением |
|
||||||||
|
|
|
|
|
|
f df |
|
||
|
|
|
|
2 |
|
||||
|
|
|
fэ |
0 |
|
|
|
, |
(11) |
|
|
|
|
2 |
|
f |
|||
|
|
|
|
|
m ax |
|
|
|
|
в котором f – измеренный фактор передачи используемого фильтра прием-
ника.
Таким образом, из формулы (10) следует, что Nmax постоянно при фикси-
рованной полосе узкополосного приемника. Кроме того, при узкой полосе спек-
тра флуктуации положение максимума функции N (V V0 ) прямо пропорционально – значению эффективного напряжения нормального шума.
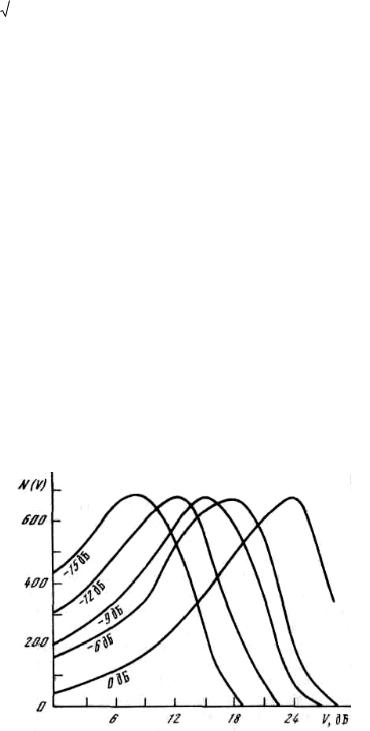
На рис. 4. для несущей частоты f = 10 МГц и fэ = 1041Гц показано семейство кривых распределения N (V V0 ) при различных значениях эффективного выходного напряжения шумового генератора.
Рис. 4. Распределения среднего числа положительных выбросов огибающей нормального шума для различных значений его интенсивности
На этом рисунке по оси ординат в линейных единицах отложены положительные выбросы огибающей нормального шума, а по оси абсцисс – селективные уровни в децибелах по отношению к эффективному напряжению, при котором было измерено распределение. Из представленного семейства кривых
8

отчетливо видно, что при постоянной энергетической полосе пропускания приемника всякое изменение уровня выхода генератора нормального шума в ту или иную сторону приводит к соответствующему сдвигу положения максимума распределения N (V V0 ) по оси абсцисс, т.е. имеет место прямо пропорциональная зависимость между этими величинами, что и следует из формулы (10).
Здесь необходимо подчеркнуть, что из формулы (10) вытекает важное для практики следствие, состоящее в том, что весьма трудоемкий прямой процесс определения энергетической полосы пропускания узкополосного приемника при отсутствии свип-генератора можно заменить простым вычислением ее по формуле
f |
э |
N |
max |
(V V ) e12 |
, |
(12) |
|
|
0 |
|
|
предварительно измерив распределение среднего числа выбросов огибающей нормального узкополосного шума, прошедшего через этот приемник.
Оценка показаний каналов анализатора в режиме измерения среднего числа положительных выбросов огибающей нормального шума
В логарифмически-квадратичных координатах
|
y* lg |
N (V V0 ) |
; |
x* V02 |
|
(13) |
|||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
V0 |
|
|
|
|
|
|
|
||
распределение |
N (V V ) |
|
|
V0 |
exp |
V02 |
|
представляется |
линейной функ- |
||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
||||||||||||||
|
0 |
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
цией с угловым коэффициентом наклона |
|
|
|
|
|
. Уклонение показаний счетчи- |
|||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
ков анализатора в режиме измерения распределения N(V>V0) для нормально-
флуктуирующего напряжения V от прямой линии в системе координат (5) говорит о нарушении работы установки в этом режиме.
9
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1.Измерение среднего числа выбросов огибающей напряжения нормального шума
1.1.Задать продолжительность измерения с помощью пульта управления на статистическом анализаторе. Время анализа выбирается порядка одной минуты, так как процесс стационарный и эргодический.
1.2.Дождаться окончания анализа и, используя пульт управления, получить данные ni по количеству превышений огибающей нормального шума для каждого порогового уровня статистического анализатора.
1.3.Полученные данные записать в табл. 1.
1.4.Рассчитать распределение среднего числа выбросов огибающей нормального шума N(V> V0) и lg (N((V> V0)) по формуле ni/T=Ni(V>V0), значения которых записать в табл. 2.
1.5.По данным табл. 2 построить график зависимости lg Ni(V> V0) от
lg V0.
1.6.Сравнить экспериментальную зависимость с кривыми на рис. 4 и сделать вывод.
2.Оценка показаний каналов анализатора в режиме измерения среднего числа положительных выбросов огибающей нормального шума
2.1.По данным табл. 2 рассчитать значения Ni(V> V0)/ V0 для каждого порогового уровня, затем по этим данным построить в логарифмическиквадратичных координатах (5) распределение среднего числа выбросов огибающей нормального шума.
2.2.По методу наименьших квадратов найти коэффициенты k и b для
формулы |
|
y=kx+b, где |
y* lg |
N (V V0 ) |
, |
x* V02 , b= |
1 |
|
. |
||
V |
0 |
2 |
2 |
||||||||
|
|
||||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
x |
|
||
2.3. Сравнить на графике кривую, полученную по методу наименьших квадратов, с экспериментальной кривой и сделать вывод.
10
