Физ.Полупр.(для студ) / ФТТ_Садыков_13-14 / FTT_Sadykov_2

2. Электронные состояния в кристалле.

Прежде чем говорить об электронных состояниях в кристалле, напомним себе, как описываются в квантовой теории свободные электроны и электроны, связанные в атоме.

Свободный электрон.

Свободный электрон с импульсом p характеризуется волновой функцией:

где V - нормировочный объем. Легко видеть, что эта функция является собственной функцией оператора импульса и одновременно собственной функцией оператора кинетической энергии (гамильтониана свободной частицы):

Энергия электрона, представленная как функция волнового вектора, называется законом дисперсии. В случае свободного электрона мы имеем дело со сферическим законом

поскольку поверхности постоянной энергии в этом случае представляют собой сферы в пространстве волнового вектора. Кроме того, эта зависимость выражает непрерывность энергетического спектра свободного электрона (для свободного электрона допустимы всевозможные значения абсолютной величины волнового вектора).

Обратим внимание, волновой функции 0k r соответствует постоянная плотность

вероятности обнаружить электрон в пределах нормировочного объема V, 0k r 2 const ,

т.е. функция 0k r описывает делокализованное состояние электрона. Эти элементарные

сведения о свойствах волновой функции свободных частиц будут использованы при

построении волновой функции электрона в кристалле.

Электрон, связанный в атоме.

Примером связанных состояний являются электронные состояния атома водорода: атом водорода содержит один электрон, волновая функция которого удовлетворяет уравнению Шредингера с атомным гамильтонианом ˆ a :

сферической системе координат как произведение радиальной и угловой частей и зависит от

квантовых чисел :

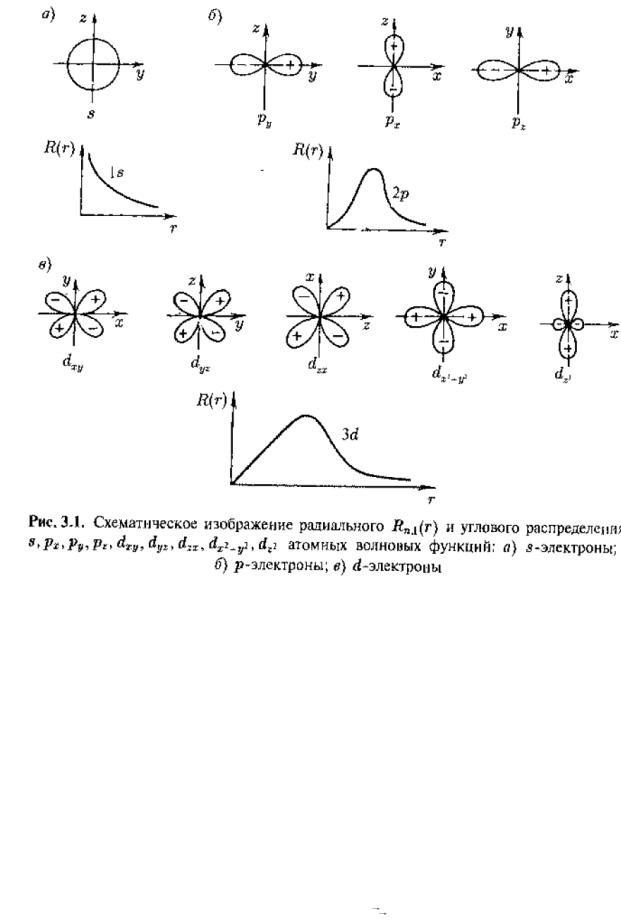
локализованное состояние электрона. На рис. 3.1 приведено распределение электронной плотности для связанных состояний электрона – атомных орбиталей (см. Атомн. Физ.).

Другая особенность связанных электронных состояний в том, что возможные собственные энергии a , энергии связи, представляют дискретный набор отрицательных значений, т.е.

энергетический спектр связанных электронов дискретный.

Состояние многоэлектронного атома описывается слэтеровским детерминантом,

составленным из одноэлектронных орбиталей типа (2.5), с учетом их вырождения по электронному спину и в соответствие с принципом Паули. Тем самым в многоэлектронном атоме выделяются внутренние электроны (с энергией связи до нескольких кэВ) и внешние

(валентные) электроны (энергии связи – десятки эВ).

Электроны в кристалле. Функции Блоха.

Теорема Блоха. Закон дисперсии.

Когда из атомов образуется кристалл, наибольшие изменения претерпевают волновые функции и собственные энергии валентных электронов. Говоря об электронных состояниях в кристалле мы в первую очередь имеем в виду такие модифицированные состояния. Самое простое предположение состоит в том, что валентные электроны атомов, образующих кристалл, теперь испытывают кулоновское поле и соседних атомов. Это, по крайней мере,

сильно уменьшает степень локализации валентного электрона вблизи отдельного ядра и способствует его поведению как свободного электрона, в пределах объема кристалла.

Руководствуясь этими соображениями, представим волновую функцию электрона в кристалле, явно выделив в ней множитель exp ikr , отвечающий волновой функции

свободного электрона:

периодом решетки. Тем самым учитывается то, что электрон распространяется не в однородном пространстве (как свободный электрон), а внутри периодической структуры.

Соотношения (2.6) и (2.7), записанные нами на основе достаточно общих соображений, на самом деле составляют содержание теоремы Блоха, а функция, удовлетворяющая этим двум условиям, называется функцией Блоха. Теорема Блоха строго доказывается методами теории групп, используя принципы трансляционной симметрии кристалла; читатель может ознакомиться с ее доказательством самостоятельно [1,3].

Перейдем к рассмотрению следствий теоремы Блоха. Производя сдвиг аргумента в (2.6) на вектор решетки и пользуясь свойством (2.7) легко получить соотношение:

откуда видно, что функция Блоха не периодична. В то же время легко видеть, что квадрат

Функции Блоха (2.6), как и функции свободного электрона (см. (2.1)), идентифицируются вектором k , который принято называть квазиволновым вектором, потому что он отличается от волнового вектора свободного электрона (см. ниже). Функция Блоха является

делокализованной, т.е. она, подобно функции свободного электрона 0k r 0p r ,

простирается по всему объему решетки.

Теорема Блоха предписывает нам искать электронные функции в кристалле в виде,

удовлетворяющем соотношениям (2.6) и (2.7). В частности, этим требованиям удовлетворяет функция, представленная как линейная комбинация атомных орбиталей (ЛКАО)

составляющих кристалл атомов:

множители, N – коэффициент нормировки. Заметим, что в (2.10) проводится суммирование по орбиталям одного и того же типа a r на всех узлах. Число различных функций Блоха,

полученных с использованием конкретной орбитали a r , равно числу физически

различных значений квазиволнового вектора k (см. ниже). Фрагмент ЛКАО,

соответствующей определенному вектору k ( k 2 ), показан на Рис. 2.1.

Линейные комбинации атомных орбиталей k r , представленные выражениями типа (2.10), должны удовлетворять уравнению Шредингера:

При записи уравнения (2.11) сделаны два предположения:

1)Адиабатическое приближение. Суть его в том, что волновая функция электрона определяется для неподвижной конфигурации ядер и движением ядер (например, их колебаниями) пренебрегается.

2)Одноэлектронное приближение. Согласно этому приближению гамильтониан ˆ Cr

зависит от координат одного электрона. Влияние других электронов на поведение

рассматриваемого электрона может быть учтено введением самосогласованного потенциала,

как это делалось при расчете одноэлектронных состояний в атоме (метод Хартри –Фока).

Гамильтониан электрона в кристалле ˆ Cr представим как сумму его кинетической энергии ˆ 0 и кристаллического потенциала VCr , который, прежде всего, представляет из себя сумму атомных потенциалов Va r l :

Помимо атомных потенциалов выражение для VCr r включает также взаимодействие

рассматриваемого электрона с остальными электронами в решетке, которое мы включим далее в самосогласованный гамильтониан (см. ниже).

Определим теперь энергию k , соответствующую состоянию k r , используя

уравнение (2.11) и представление блоховской функции в виде (2.10). Полезно

очередь учитывает влияние атомных потенциалов соседних узлов. Кроме этого будем считать, что сюда же включен самосогласованный потенциал взаимодействия электронов, о

котором говорилось выше. Если считать, что основное взаимодействие электрона обусловлено атомными потенциалами соседних узлов, то W 0 . С учетом сказанного результат действия оператора ˆ Cr на орбиталь l -ого узла a r l можно представить

как:

ˆ Cr a r l ˆ a W a r lEa a r l W a r l .

Тогда уравнение (2.11) можно представить (после умножения обеих частей выражения слева на a r ) как:

атомных орбиталей, центры которых отстоят друг от друга на вектор решетки l .

для случая, когда перекрывающиеся орбитали локализованы на соседних узлах, т.е. l a ,

a - постоянная решетки.

Распишем выражение (2.13) для простой кубической решетки Бравэ. В знаменателе под суммой (2.13) оставим только слагаемые с l 0 , а в числителе – слагаемые с l 0 и l a . Тогда энергия блоховского состояния Ek , как функция квазиволнового вектора k

(закон дисперсии k ), запишется как:

Ek k a A 0 2A a cos kxa cos kya cos kza . (2.14)

произвольные целые числа. Это соотношение в представлениях обратной решетки (в данном случае для кубической решетки) выглядит как k k g . Отсюда следует вывод,

что блоховские функции, соответствующие квазиволновым векторам k и k g - это одно и

то же состояние. Поэтому областью определения множества различных блоховских функций

решетки. Как было отмечено в Разд.1, элементарная ячейка обратной решетки, построенная методом Вигнера-Зейтца, называется 1-ой зоной Бриллюэна. В случае простой кубической решетки 1-ая зона Бриллюэна определяется как:

т.е. она представляет из себя куб с ребром 2 a

2. Из закона дисперсии видно, что для функций типа (2.10) ширина полосы (зоны)

разрешенных значений энергии равна 12 A a . Поскольку значение интеграла переноса

энергий будет тем больше, чем менее локализованы атомные орбитали. Следовательно,

функциям (2.10), построенным на орбиталях внешних (валентных) электронов в атоме,

соответствует зона разрешенных энергий большей ширины (см. рис.2.2).

3. Теперь выясним, каково число значений квазиволнового вектора k в пределах 1-ой

зоны Бриллюэна (или каково число физически различных блоховских состояний). Для этого рассмотрим кристалл кубической симметрии в виде прямоугольного параллелепипеда,

(условия Борна-Кармана). Циклическое граничное условие по направлению оси x означает,

что поведение функции Блоха на поверхности кристалла x 0 идентично ее поведению на противоположной поверхности x Nxa , что выражается первым равенством в (2.16). Но исходя из свойств функций Блоха (см. (2.8)), сдвиг аргумента блоховской функции порождает фазовый множитель (второе равенство в (2.16)).

внимание на то, что при построении функций Блоха в виде ЛКАО было использовано именно N атомных орбиталей (на N узлах). Иными словами, при переходе от атомных орбиталей к функциям Блоха выполняется правило сохранения числа физически различных

электронных состояний системы. Важно заметить, что возможные значения квазиволнового вектора равномерно заполняют I-ую зону Бриллюэна и на один волновой вектор приходится

объем: V . Поскольку для макроскопических образцов

N Nx Ny Nz имеет порядок числа Авогадро, возможные значения квазиволнового вектора образуют квазинепрерывное множество. Это дает нам основание рассматривать закон

дисперсии как скалярную функцию непрерывных переменных (или векторного

аргумента k ).

Как соотносятся энергии разрешенных зон с энергиями одноэлектронных атомных орбит, из которых составлены блоховские состояния, представлено на Рис.2.2. Мы видим,

что дискретные энергии связанных в атоме электронов уширяются в энергетические зоны по

мере уменьшения расстояния между атомами a до значения постоянной решетки a0 .

Уширение зоны разрешенных энергий, как легко заметить из (2.14), является результатом перекрытия атомных орбиталей. С другой стороны, это же уширение - следствие

делокализации электронов в пределах кристалла.

Использованный нами метод построения функций Блоха, как ЛКАО (см. (2.10)),

называют методом сильной связи. Этим подчеркивается, что вблизи каждого узла волновая

функция электрона может быть приближенно представлена атомной орбиталью,

описывающей связанное состояние электрона в свободном атоме.

Выше мы пришли к выводу, что множество блоховских функций кристалла может быть задано в пределах одной элементарной ячейки его обратной решетки (1 – ой зоны Бриллюэна). Такое описание электронных состояний известно как схема приведенных зон. В

то же время иногда бывает удобно пользоваться схемой расширенных зон. Это делается

Эффективная масса.

Закон дисперсии (2.14), рассматриваемый как непрерывная функция квазиволнового вектора k , может быть упрощен для малых векторов k , если воспользоваться разложением

Введенный параметр m называют эффективной массой. Действительно, закон дисперсии в виде (2.17) – это закон дисперсии «свободной» частицы с массой m . Согласно

(2.17) постоянной энергии E k const соответствует сферическая поверхность в

пространстве волнового вектора, поэтому выражение (2.17) известно как закон дисперсии в

сферическом приближении. Очевидно, изоэнергетические кривые в плоскости (например, в

плоскости kz 0 ) в данном случае представляют собой окружности. С ростом волнового вектора, с приближением к границам 1-ой зоны Бриллюэна, поверхности постоянной энергии отличаются от сфер (см. Рис. 2.3a), а изоэнергетические кривые в плоскости, - от окружностей (см. Рис.2.3б).

Закон дисперсии может быть представлен также в одномерном случае, как изменение энергии с изменением волнового вектора в определенном направлении. Например, Рис.2.3в

представляет зависимость полученного нами закона дисперсии (2.14) от kx при постоянстве двух других составляющих волнового вектора.

Введение функций Блоха и определение закона дисперсии для электронов в кристалле посредством метода ЛКАО достаточно убедительно демонстрируют характер модификации электронных состояний валентных электронов свободных атомов при их конденсации в кристалл и их энергий. Однако более важной является задача количественного определения закона дисперсии для электронов в кристалле. Именно закон дисперсии конкретного соединения во многих случаях определяет его физические свойства, его пригодность в качестве рабочего материала для создания функциональных приборов. Метод ЛКАО с этой точки зрения не является достаточно точным методом. Поэтому для вычисления закона дисперсии материалов обычно используется большое разнообразие численных методов: