новая папка 1 / 702911

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ

__________________________________________________________________________________________________

БУКИНА Н.В,

СИДЕЛОВ Д.И.

ИЗБРАННЫЕ МЕТОДЫ РЕШЕНИЯ ФИЗИЧЕСКИХ ЗАДАЧ

(методическое пособие)

________________________________

Оренбург 2019

ускорение и время.

С точки зрения классификации методов, графический метод решения задач относится к теоретическим [1], т.к. при его использо-

вании мы не производим измерений.

Рассмотрим применение интегральных представлений при решении механических задач графическим методом на конкретных примерах.

Решение задач механики графическим методом

Задача 1, [2]

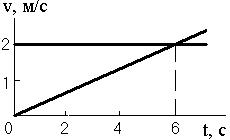
Две частицы в момент времени t 0 вышли из одной точки и движутся вдоль одной прямой. По графикам зависимости скорости от времени определите координаты и время новой встречи частиц.

При решении данной задачи можем воспользоваться одной из перечисленных выше интегральных зависимостей скорости от вре-

мени и учесть, что частицы снова встретятся в момент времени, со-

ответствующий одинаковым площадям под прямыми. Из графиков видно, что одна из частиц движется равномерно, а вторая ускоренно,

без начальной скорости. Перемещению первой частицы будет соот-

ветствовать площадь прямоугольника 0 2 С 12 , а перемеще-

нию второй частицы – площадь треугольника 0 В 12 .

2

Площади этих двух фигур будут равны только в случае равен-

ства треугольников А02 и АВС. Из этих рассуждений ясно, что частицы снова встретятся через 12 секунд после начала движения.

Задача 2, [2]

Тело в течение времени t0 движется с постоянной скоростью v0 . Затем скорость его линейно нарастает со временем так, что в мо-

мент времени 2t0 она равна 2v0 . Определите путь, пройденный те-

лом за время t t0 .

Нарисуем график зависимости скорости от времени по данным

задачи.

Воспользуемся пропорциональной зависимостью скорости от времени:

3

Пути, пройденному телом за время t t0 , можно сопоставить площадь сложной фигуры 0 v0 A B t . Эта площадь состо-

ит из площадей двух прямоугольных треугольников А 0 v0 и

0 B t . Общую площадь можно вычислить по формуле:

Окончательный ответ можно привести к более симметричному

виду

S v0 t 2 t 2 .

2t0 0

Графический метод решения задач иногда позволяет получить ответ, не прибегая к рутинным вычислениям. В качестве примера приведем элегантное графическое решение задачи, которая при ал-

гебраическом подходе потребует вполне ощутимых затрат времени и сил.

Задача 3

Доказать, что пути, пройденные телом за одинаковые проме-

жутки времени при прямолинейном равноускоренном движении без начальной скорости соотносятся как ряд нечетных чисел, т.е.

S1 : S2 : S3: 1: 3: 5

Нарисуем график зависимости скорости тела от времени. Пу-

ти, пройденные телом за одинаковые промежутки времени будут изображаться как треугольник и прямоугольные трапеции, каждую из которых можно разбить на одинаковые треугольники площади S1 .

4

Из рисунка видно, что площади треугольника и трапеций со-

относятся как ряд нечетных чисел S1 : S2 : S3: 1: 3: 5

В некоторых случаях графический метод может «спасти» нас от, казалось бы, неизбежного интегрирования.

Задача 4, [2]

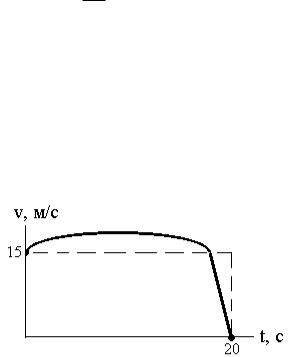
График зависимости скорости тела от времени имеет вид по-

луокружности. Максимальная скорость тела v0 , время движения t0 .

Определите путь, пройденный телом за время t0 .

Начальные условия в графическом изображении выглядят сле-

дующим образом:

На первый взгляд может показаться, что при решении этой за-

дачи необходимо использовать формулу площади круга, но если мы изменим единицы измерения одной из величин, то вид кривой зави-

симости поменяется, и окружность превратится в эллипс. Исходя из этих рассуждений нам нужно применять формулу половины площа-

ди эллипса: S ab / 2, где a и b – полуоси эллипса. Окончатель-

ный ответ примет вид:

S v0t0 . 4

5

Задача 5, [2]

Автобус движется в течение 20 с по прямой до остановки,

проходя при этом расстояние 310 м. Его начальная скорость 15 м/с.

Докажите, что ускорение автобуса меняется по направлению.

Для решения этой задачи нам понадобятся как интегральные представления, так и дифференциальные. Суть дифференциального представления состоит в следующем. Если мы имеем дифференци-

альную связь между тремя физическими величинами:

С dBdA ,

где физическая величина A f (B) является функцией от B . Тогда тангенс угла наклона касательной к графику зависимости A A(B) в

каждой точке B будет давать значение физической величины С .

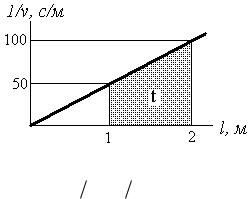
Нарисуем примерную зависимость скорости от времени в про-

цессе, описанном задачей.

Даже если бы, двигаясь сначала равномерно, автобус мог по-

том остановиться за бесконечно малое время, то он прошел бы толь-

ко 300 м (площадь прямоугольника, ограниченного пунктирной ли-

нией), вместо 310, требуемых условиями задачи. Значит, чтобы ус-

петь пройти требуемое расстояние, автобус должен вначале двигать-

ся ускоренно, но по условиям, он должен остановиться, т.е. в неко-

торый момент времени автобус будет замедлять свою скорость, а это означает смену направления ускорения автобуса. На графике это

6

выражается сменой знака тангенса угла наклона касательной к гра-

фику зависимости скорости от времени (вначале движения автобуса угол между касательной и осью времени – острый, а в конце движе-

ния – тупой).

Иногда сразу бывает неясно, каким образом применить графи-

ческий метод при решении задачи.

Задача 6, [3]

Муравей бежит от муравейника по прямой так, что скорость его обратно пропорциональна расстоянию до центра муравейника. В

какое время муравей добежит от точки А до точки В, которая нахо-

дится на расстоянии l2 2 м от центра муравейника.

Поскольку скорость муравья обратно пропорциональна рас-

стоянию до центра муравейника, попробуем построить график зави-

симости 1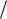v f (l) . Площадь заштрихованной трапеции будет яв-

ляться искомым временем движения муравья.

По формуле площади трапеции можно легко определить t :

Задача 7, [2]

Тело начинает движение из точки А и движется сначала рав-

ноускоренно в течение времени t0 , затем с тем же по модулю уско-

7

рением – равнозамедленно. Через какое время от начала движения тело вернется в точку А.

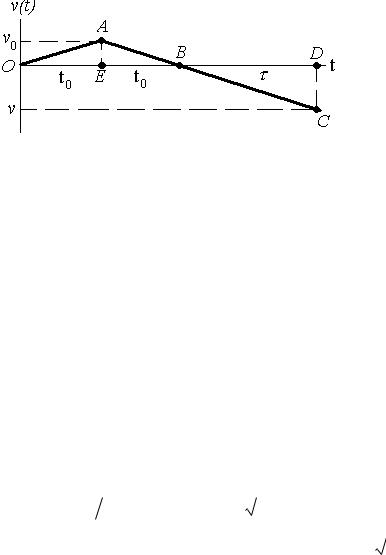
Нарисуем график зависимости скорости от времени.

После изменения направления ускорения, тело должно про-

должать движение в том же направлении до полной остановки, при-

чем, т.к. ускорение по абсолютной величине не изменяется, то время остановки равно времени разгона t0 . Расстояние, пройденное телом в прямом направлении численно равно площади OAB , который лежит над осью времени, а в обратном направлении – площади пря-

моугольного BCD , лежащего под осью времени. Значит площадь

OAB равна площади BCD . Поскольку OAE BAE , то пло-

щадь BAE равна половине площади BCD . Известно, что площа-

ди подобных фигур соотносятся как квадраты линейных размеров,

Попробуем применить графический метод к решению задач динамики.

Задача 8, [2]

На покоящееся тело массы m1 налетает со скоростью v тело массы m2 . Сила, возникающая при взаимодействии тел, линейно за-

висящая от времени, растет от нуля до значения F0 за время t0 , а за-

тем равномерно убывает до нуля за то же время t0 . Определите ско-

8

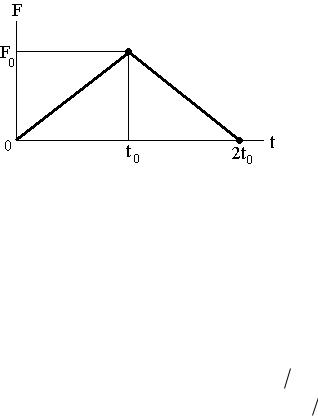
рости тел после взаимодействия, считая, что все движения происхо-

дят по одной прямой.

Взаимодействующие тела образуют замкнутую систему, в ко-

торой должен выполняться закон сохранения импульса. Изменение импульса каждого из тел будет численно равно импульсу дейст-

вующей во время удара силы. Этот импульс силы численно равен площади треугольника под графиком F0t0 . Исходя из этого, можно записать:

Задача 9, [2]

Сила, действующая на снаряд массы m в стволе орудия нарас-

тает равномерно от нуля до F0 на участке ствола l1 , не меняется на участке ствола длины l2 и, наконец, равномерно уменьшается до ну-

ля на участке ствола длины l3 . Какова скорость снаряда при вылете из ствола.

9