новая папка 1 / 270286

7.Математическое ожидание и дисперсия случайной величины.

Математическим ожиданием дискретной случайной величины называется сумма произведений значений случайной величины на вероятность этих значений.

М(х) =х1 р1 +х2 р2 +…+хn рn

Решение. Математическое ожидание дискретной случайной величины: М(х) = 3 0,1+ 5 0,6 + 2

0,3 = 3,9.

Понятие математического ожидания случайной величины распространяется и на непрерывную случайную величину.

Пусть f(x) плотность вероятности случайной величины Х. Тогда Математическим ожиданием непрерывной случайной величины Х, все значения которой принадлежат отрезку [а,

в ] называют определённый интеграл

М(х) = х f(x) dx.

Пример 9. Найти математическое ожидание случайной величины Х, если известна функция распределения этой величины

Решение. Найдём сначала плотность распределения вероятностей этой величины f(x) = F (x).

Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

D(x) = M[ X – M(x) ]2.

11

Показать, что f(x) может служить плотностью вероятности некоторой случайной величины Х. Найти математическое ожидание случайной величины Х.

Решение. Так как все возможные значения случайной величины принадлежат интервалу (а,в), то должно выполняться соотношение

Р0,3 0,5 0,2

Решение. Дисперсия дискретной случайной величины

D(x)= М( Х-М(х) )2 .

Найдём математическое ожидание:

М(х)= 1 0,3+ 2 0,5 + 5 0,2 =2,3.

Найдём все возможные значения квадрата отклонения:

(х1 –М(Х) )2 =(1 – 2,3)2= 1,69;

(х2 - М(Х) )2 =(2 – 2,3)2= 0,09; (х3 - М(Х) )2 =(5 - 2,3)2= 7,29.

Напишем закон распределения квадрата отклонения:

Дисперсия есть математическое ожидание квадрата отклонения:

D(X)= 1,69 0,3 + 0,09 0,5 + 7,29 0,2 = 2,01.

Рассмотрим формулу, которая приводит к цели значительно быстрее:

Дисперсия равна разности между математическим ожиданием квадрата случайной величины

Х и квадратом её математического ожидания:

D(X) = М(Х2) – (М(Х))2.

Пример12. Найти дисперсию случайной величины Х , которая задана следующим законом

Решение.

Найдём математическое ожидание М(Х):

М(Х) = 2 0,1+ 3 0,6 + 5 0,3 = 3,5.

Найдём закон распределения случайной величины Х2:

12

Найдём математическое ожидание М(Х2):

М(Х2)= 4 0,1 + 9 0,6 + 25 0,3 = 13,3.

Искомая дисперсия:

D(X) = М(Х2) – (М(Х))2=13,3 – (3,5)2= 1,05.

Пример 13. Если математическое ожидание квадрата случайной величины, заданной законом

Р0,5 0,2 0,3 ,

Равно М(Х2) = 2,3 , тогда дисперсия равна? Решение.

М(Х) = -2 0,5+ 0 0,2 + 1 0,3 = -0,7; ( М(Х))2 = 0,49;

D(X) = 2,3 – 0,49 = 1,81.

Пример 14. Математическое ожидание дискретной случайной величины, заданной законом распределения,

Р0,2 0,3 0,5 , равно?

Решение. М(Х) = 2 0,2 + 5 0,3 + 8 0,5 = 0,4 + 1,5 + 4= 5,9.

Пример 15. . Математическое ожидание непрерывной случайной величины, заданной плотностью распределения,

Пример 16. Закон распределения вероятностей дискретной случайной величины Х имеет вид:

13

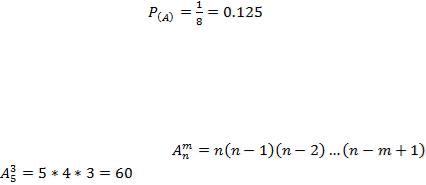
Практическое занятие по теме

Задание №1

В больнице 9 больных с заболеванием K и 6 больных с заболеванием L. Случайным образом принимают на осмотр. Вероятность того, что на осмотр придет больной с заболеванием L равна…. Решение:

Так как вероятностью Р(А) события А, связанного с опытом с равновероятными исходами, называется отношением числа исходов благоприятствующих событию А, к числу всех исходов

. следует, что n – количество всех исходов (9+6), m – количество благоприятных исходов.

Отсюда следует, что

Ответ: 0,4.

Задание №2

В ящике шары с номерами от 1 до 8. Вынимают наудачу один шар. Вероятность, что он имеет номер 4 равна… Решение:

Так как вероятностью Р(А) события А, связанного с опытом с равновероятными исходами, называется отношением числа исходов благоприятствующих событию А, к числу всех исходов

. следует, что n – количество всех исходов, m – количество благоприятных исходов.

Отсюда следует, что

Ответ: 0,125

Задание №3

Количество способов выбора 3 делегатов на конференцию из 5 студентов равно… Решение: !сочетания

Так как размещением называют множества, состоящие из n различных элементов по m, которые различаются либо составом элементов, либо их порядком. Число всех возможных размещений

Задание №4

Количество пятизначных чисел, составленных из цифр 1,2,3,4,5 без повторения равно… Решение:

Так как множество элементов, состоящих из одних и тех же различных элементов и отличающихся друг от друга только порядком следования, называются перестановками этих элементов. Число всевозможных перестановок из элементов вычисляют по формуле:

, следует, что n=5;

Ответ:120.

Задание №5

В коробке 16 дискет, 4 из которых не содержат информации. Наудачу программист берет одну дискету. Вероятность того, что дискета содержит информацию, равно… Решение:

Так как вероятностью Р(А) события А, связанного с опытом с равновероятными исходами, называется отношением числа исходов благоприятствующих событию А, к числу всех исходов

14

. следует, что n – количество всех исходов, m – количество благоприятных исходов.

Отсюда следует, что

Ответ: 0,75.

Задание №6

Количество способов составления списка из 6 выступающих равно… Решение:

Так как множество элементов, состоящих из одних и тех же различных элементов и отличающихся друг от друга только порядком следования, называются перестановками этих элементов. Число всевозможных перестановок из элементов вычисляют по формуле:

, следует, что n=6;

Ответ:720.

Задание №7

В ящике 8 годных и 2 бракованных детали. Рабочий берет наудачу одну деталь. Вероятность того, что деталь окажется годной, равна… Решение:

Так как вероятностью Р(А) события А, связанного с опытом с равновероятными исходами, называется отношением числа исходов благоприятствующих событию А, к числу всех исходов

. следует, что n – количество всех исходов, m – количество благоприятных исходов.

Отсюда следует, что Ответ: 0,8

15

8.Основные формулы

Закон распределения дискретной величины – соответствия между значениями х. , х. ,… х. этой величины и их вероятностями р , р ,…р

Р =1

Функция распределения F(x)=P(X<x), где P(X<x) – вероятность того, что случайная величина Х примет значение, меньшее х.

Вероятность, того, что случайная величина х примет значение, Принадлежащее интервалу (а,б) определяется равенством:

Математическое ожидание непрерывной случайной величины (где возможные значения Х принадлежат (а,б))

М(x)= x f(x) dx

Дисперсия, или рассеяние, случайной величины Х – математическое ожидание квадрата её отклонения:

9.Список литературы

1.В.Е. Гмурман «Теория вероятностей и математическая статистика».

2.В.Е. Гмурман «Руководство к решению задач по теории вероятностей и математической статистике».

3.П.Е.Данко, А.Г.Попов, Т.Я.Кожнвникова «Высшая математика в упражнениях и задачах».

4.А.А.Гусак, Е.А.Бричикова « Теория вероятностей».

16