
новая папка 1 / 315553
.pdfМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования «Калмыцкий государственный университет»
ТЕОРЕТИЧЕСКИЙ МИНИМУМ ПО РАЗДЕЛУ «МЕХАНИКА» КУРСА ОБЩЕЙ ФИЗИКИ
Методические указания для студентов 1 курса направлений «Физика» и «Химия, физика и механи
ка материалов» факультета математики, физики и информационных тех нологий
Элиста 2013
Составитель В.А. Очиров
Теоретический минимум по разделу «Механика» курса общей физики: Методические указания для студентов 1 курсов направлений «Физика» и «Химия, физика и механика материалов» факультета математики, физики и информационных технологий / Калм. ун-т; Сост. В.А. Очиров. - Элиста 2013
-30 с.
Вработе приведены тезисы лекций по разделу «Механика» университет ского курса общей физики, представлен справочный материал по изучаемым темам.
Пособие предназначено для студентов первых курсов направлений «Фи зика» и «Химия, физика и механика материалов» факультета математики, фи зики и информационных технологий.
Утверждено учебно-методической комиссией факультета МФИТ
Рецензент канд. физ.-мат. наук, доцент Р.А. Бисенгалиев
Подписано в печать 25.04.13. Формат 60x84/16. Печать офсетная. Бумага тип. № 1. Усл. п. л. 1,86. Тираж 100 экз. Заказ 2104.
Издательство Калмыцкого университета. 358000 Элиста, ул. Пушкина, 11
ТЕОРЕТИЧЕСКИЙ МИНИМУМ ПО РАЗДЕЛУ «МЕХАНИКА» КУРСА ОБЩЕЙ ФИЗИКИ
Тема 1. Введение в физику
Встречаясь в окружающем мире с различными физическими объектами, явлениями, ситуациями и связями между ними, человек создаёт в своём соз нании модель, которая состоит из образов этих объектов, явлений, ситуаций и связей между ними, а также правил оперирования с ними.
При изучении физики как науки важно всегда иметь в виду модельный ха рактер её построений. Задача физики состоит в том, чтобы создать в нашем сознании такую картину физического мира, которая наиболее полно отражает свойства мира. Поскольку реальный физический мир очень многообразен, при создании моделей нужно принимать во внимание только существенные для данного круга явлений свойства и связи.
Физические модели являются приближёнными моделями и справедливы в некоторых пределах применимости. Один и тот же физический объект в раз ных ситуациях может быть представлен различными моделями. Научные ис следования постоянно расширяют и углубляют физическую модель мира. Это можно сделать в результате эксперимента и наблюдения. Необходимо забо титься, чтобы каждый элемент изучаемой модели имел четко определенное содержание и ясно сформулированное соотношение с элементом реального физического мира.
В познании физического мира вначале устанавливаются различия между объектами, затем идет сравнение их между собой по каким - то признакам, свойствам, а в конце измеряются эти физические свойства. Измерение сво дится к сравнению измеряемых свойств со свойством, принятым за единицу. Свойства, качества и т.д., которыми оперирует физика, называются физиче скими величинами. Задача измерения сводится к нахождению численного значения физической величины.
Между различными физическими величинами существуют многообразные связи, с их помощью одни физические величины можно выразить через дру гие. Можно ограничиваться небольшим числом физических величин, через единицы которых можно выразить все остальные. Эти единицы называются основными, а совокупность единиц физических величин - системой единиц. В качестве основных берутся единицы длины, массы, времени и т.д. Системы единиц отличаются друг от друга практической целесообразностью и удобст вом. В результате длительного обсуждения все страны в 1961г. пришли к за ключению, что наиболее целесообразной является Международная система единиц (СИ). В СИ в качестве основных взяты единицы длины - метр, массы - килограмм, времени - секунда, силы тока - ампер, температуры - кельвин, силы света - кандела.
:
Тема 2. Пространство и время
Все материальные тела имеют протяженность, занимают определенное место и располагаются определенным образом друг относительно друга. Эти общие свойства материальных тел в сознании человека отразились в виде по нятия пространства, а математическая формулировка этих свойств была вы ражена в виде системы геометрических понятий и связей между ними. Про странство, в котором мы живем, является трехмерным. Положение точек в нем характеризуется тремя числами. Какими именно числами, зависит от сис темы координат, с помощью которой описывается положение точек про странства.
При изучении раздела «Механика» необходимо знать следующие системы координат:
1) на плоскости: а) прямоугольная декартова, в которой двумя числами (х, у), характеризующими положение точки, являются длины х и у; б) полярная, в которой двумя числами (р, ф), характеризующими положение точки, явля ются длина р и угол ср;
2) в пространстве: а) прямоугольная декартова, в которой тремя числами (х, у, г), характеризующими положение точки, являются длины х, у и ъ (суще ствуют правая и левая система координат); б) цилиндрическая, в которой тремя числами (р, ср, г), характеризующими положение точки, являются дли на р, угол ф и длина ъ; в) сферическая, в которой тремя числами (г, ф, 9), ха рактеризующими положение точки, являются длина г, углы ф и 6. К указанным выше системам координат необходимо дать рисунки.
Понятие времени.
Общие свойства развивающегося, изменяющегося мира в сознании чело века отразились в виде понятия времени. Под временем понимается свойство материальных процессов иметь определенную длительность, следовать друг за другом в определенной последовательности и развиваться по этапам и сту пеням. Время является формой существования материи, они неразрывны. Процессы эти нужно рассматривать во взаимосвязи - в этом физический смысл понятия времени.
Периодические процессы.
В природе обращают на себя внимание в первую очередь повторяющиеся процессы: повторение дней и ночей, времён года, движение звезд по небосво ду, биение сердца, дыхание и т.п. Изучение и сравнение их между собой при вело к идее длительности материальных процессов, а сравнение длительно стей - к идее их измерения.
Принятый за эталон периодический процесс называется часами. Часы должны иметь одинаковый темп хода в различных точках системы отсчета. Синхронизацию часов проводят с помощью световых сигналов по формуле
I = 1о+з/с, где с - скорость света.
Система отсчета включает реальное твердое тело (тело отсчета) по отно шению к которому рассматривается движение исследуемой материальной
точки. С системой отсчета жестко связывается выбранная система координат, а также часы для отсчета моментов времени, соответствующих различным положениям движущейся материальной точки. Векторные и координатные методы описания.
а) в координатной форме положение материальной точки определяется тремя координатами, обозначим их как хь х2, х3. Это означает для декартовых координат: хг = х, х2 = у, х3 = г; для цилиндрических: х, = р, х2 = ф, х3 = г\ для сферических X] = г, х2 = ф, х3 = в. При движении точки эти координаты меня ются, т.е. являются функциями времени: Х]=Х1(1:), х2=х2(г), х3=х3(1).
б) в векторной форме положение материальной точки может быть задано с помощью радиусавектора г относительно некоторой точки, принятой за на чало. При движении точки радиус вектор Г непрерывно меняется: г = Г(х). В декартовой системе координат Т (г) =Тх(1)+)у(1)+к г (I)
Тема 3. Кинематика материальной точки
Часть механики, изучающая движение материальных тел в пространстве и времени без рассмотрения вызывающих это движение взаимодействий, назы вается кинематикой.
Движущееся тело обладает определенными размерами -протяжённостью в пространстве. Любое движение также происходит в какой то части простран ства, размер которой называют масштабом движения. При изучении движе ния тел удобно ввести понятие материальной точки как научной абстракции.
Материальной точкой называют тело, размеры которого пренебрежимо малы по сравнению с масштабом движения. Например, можно Землю мыс ленно расчленить на отдельные части, размеры которых пренебрежимо малы по сравнению с масштабом движения, т.е. на отдельные материальные точки. Зная движение всех этих материальных точек, будем знать и движения всей системы материальных точек, т.е. земного шара.
Перемещение.
Вектор перемещения материальной точки Д г = г (г+Дх)- г (I) численно равен расстоянию между конечной и начальной точками, направлен от на чальной к конечной.
Скорость.
Вектор средней скорости о при перемещении между двумя точками
совпадает по направлению с перемещением и равен по модулю вектору пере |
|
мещения, делённому на время перемещения: бС„(1Д+Д1)=—. |
|
срУ |
ы |
Д? _& Мгновенная скорость й(х) = | ? т Т Г ~~Т
5

В декартовой системе координат о = — = 1—+7— + ^— ™А ;, = —
л а ] лг л ' г д е °* л'
оу |
|
, и. - ~ - проекции скоростей на оси. |
|
Ускорение.
Ускорением называют изменение скорости за промежуток времени Лг.
Среднее ускорение а (г,т+ Лг) = |
|
. Мгновенным ускорением называется |
|
уА1
векторная величина а, характеризующая быстроту изменения скорости дви
жущейся точки и равная первой производной от скорости по времени: ,. ДО <Ю
а= 1щ1 — = —
|
в |
|
„ |
., |
ао ~й х |
-.й у |
, с122 |
|
|
В |
декартовой |
системе координат |
а=——I—^- + ^—— + к——, где |
||||
|
|
|
|
|
л |
Л2 |
Л2 |
Л2 |
|
с!2х |
а2у |
й27. |
|
|
|
|
|
ах |
|
т-, |
а = — — , |
а,-——, - проекции ускорения на оси. При движении |
||||
|
||||||||
материальной точки по криволинейной траектории вектор полного ускорения а разлагается на составляющие: нормальное аа и тангенциальное а%. Нор мальное ап направлено к центру кривизны, а тангенциальное ах направлено по касательной к траектории точки.
Полное ускорение а=И—+т—, а модуль а = I — + —
к л у{к) {ж
Тема 4. Преобразования Галилея
Рассматриваются две инерциальные системы координат, одна из них обо значается К(х,у,г) условно неподвижная, а другая к'(х',у',г') движущаяся со скоростью б относительно системы К. Во всех инерциальных системах коор динат механические явления протекают одинаково - это утверждение называ ется принципом относительности Галилея. Существуют бесчисленное множе ство инерциальных систем координат. Все эти системы движутся поступа тельно равномерно и прямолинейно друг относительно друга.
Движущаяся система координат К' в каждый момент времени занимает определенное положение относительно неподвижной К. Формулы преобразо ваний Галилея имеют вид: х = х' + VI', у—у', г = г' X = V
х' = х-VI,у' = у, г' = г, 1 = 1.
Величины, числовые значения которых не изменяются при преобразова нии координат, называются инвариантами преобразований.
Абсолютный характер понятия одновременности.
События, одновременные в одной системе, одновременны и в другой, т.е. утверждение об одновременности двух событий имеет абсолютный характер, не зависимый от системы координат.
Инвариантность длины.
Длина тела в системах координат К и К одинакова и связана соотношением
С |
=М-х'1)1+(у,г-У1У+{г,1-2[У = ^Х1-Хх)2+(у2-у,)2+{г2-ч)2= V |
Инвариантность интервала времени.
Лг' = г'2 - 1*1 -интервал времени протекания события в системе К' Лг = 1г - и - интервал времени протекания того же события в системе К.
Интервал времени является инвариантом преобразований Галилея, т.е.
Лг = г2 - г, = г'2 - г'1 = Лг' Инвариантность ускорения.
Ускорение инвариантно относительно преобразований Галилея
Л _ Л ^ й2у _Л2у' Л2 г __А27.'
Л2 Л2 ' Л2 Л2 ' Л2 Л2
Закон сложения скоростей.
Формулы сложения скоростей имеют вид:
их = их< + V, и у = и у , и2 = и,-
Тема 5. Динамика материальной точки
Силы и взаимодействия.
В динамике Ньютона не скорость, а изменение скорости, т.е. ускорение, имеет причину. Причиной изменения скорости является сила. Количествен ную формулировку соотношения между силой и ускорением дают законы движения Ньютона. Силы создаются материальными телами. Посредством сил материальные тела взаимодействуют. Сила при этом выступает как век торная количественная мера интенсивности взаимодействий.
I закон Ньютона.
Его формулировка такова: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние. Выполняется закон в ИСО и называется законом инерции. Свойство тел сохранять состояние равномер ного и прямолинейного движения называется инерцией.
Опытным путем установлено, что система отсчета, центр которой совме щен с Солнцем, а оси направлены на соответствующим образом выбранные звезды, является инерциальной. Ее называют гелиоцентрической системой отсчета. Земля вращается вокруг своей оси и движется относительно Солнца и звезд по криволинейной траектории, имеющей форму эллипса. Криволи нейное движение всегда происходит с некоторым ускорением. Следователь но, система отсчета, связанная с земной поверхностью относительно гелио центрической системы отсчета не является инерциальной. Ускорение этой
7

системы настолько мало, что и эту систему отсчета можно считать инерциальной, ее называют геоцентрической системой отсчета.
тт |
тт |
? |
дй р |
с1(тй) |
р, |
ар |
II закон Ньютона: |
та = Р, |
т— = Р, |
^- |
' = Р, |
~=Р - скорость изме |
|
нения импульса тела равна действующей на тело силе Р. Сила измеряется в
Ньютонах.
III закон Ньютона: утверждает, что силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению: Р\2 =-Р~2\-
Рассмотрим взаимодействие двух положительных зарядов д} и д2, движу щихся со скоростями К| и V 2- Как известно, движущиеся заряды создают магнитные поля. Таким образом, в этом примере на заряды действуют как ку-
лоновские силы, так и силы Лоренца: Р{ = Р{к + Р{т , Р{ = Щ, + Р{т , но /\ Ф -Р-1, т.е. третий закон Ньютона не выполняется.
Тема 6. Законы сохранения
Законы сохранения позволяют рассмотреть общие свойства движения без решения уравнений и детальной информации о развитии процессов во времени.
Уравнения движения являются уравнениями изменения физических вели чин во времени и пространстве.
В механике законы сохранения в математическом смысле сводятся к пер вым интегралам уравнений движений.
Значение сохраняющихся величин играет важную роль и за пределами ме ханики. Сохраняющиеся физические величины являются фундаментальными, а их законы сохранения - фундаментальными законами физики.
Система материальных точек или материальная точка называется изоли рованной, если отсутствуют внешние силы. Это возможно только в том слу чае, если материальное тело в некоторой области космического пространства, очень далеко удалено от массивных небесных тел.
Закон сохранения импульса. |
|
Если система изолирована, |
то внешние силы отсутствуют, т.е. Р = О. |
,, |
ф |
Уравнение движения принимает вид: -*— = 0, т.е. р = соп$1.
Л
Импульс изолированной системы не изменяется при любых процессах, происходящих внутри системы - это закон сохранения импульса.
Внешние силы могут действовать в определенных направлениях, а в дру гих отсутствуют. Например, нет сил в направлениях, параллельных плоскости (X, У), т.е. Рх = О, Р^ = О, Р2 Ф 0. Тогда уравнение движения по осям координат имеет вид:
йрх |
йру |
ф г |
Л |
Л |
Л |
В этом случае Рх = сот(, Ру = сот1. Для этих проекций закон сохранения импульса выполняется.
Закон сохранения момента импульса.
Для изолированных систем момент внешних сил М = 0 и уравнение мо-
мента импульса принимает вид: — = 0 , 1= сопл. Момент импульса изолиро-
<М
ванной системы не изменяется при любых процессах, происходящих внутри системы - это закон сохранения момента импульса. Этот закон может выпол няться и для частично изолированных систем.
Закон сохранения энергии.
т0»2х2 |
тои\ |
= |
\ргск. Изменение кинетической энергии материальной |
|
|
|
|||
2 |
1 |
{ |
|
|
точки при ее перемещении между двумя положениями равно работе, совер шенной при этом силой.
Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается постоянной:
|
Е = Т+11= сот(. , |
2 |
х, |
Работа сил Л(--9-^) = Рхс1х; А = \рхск |
|
2 |
х, |
Потенциальные силы.
Силы, работа которых зависит лишь от начальной и конечной точек траек тории, но не зависит от ее вида, называются потенциальными. К этим силам относятся силы тяготения.
Физический смысл имеет не само значение потенциальной энергии, а лишь разность потенциальных энергий между двумя точками. Процедура придания потенциальной энергии однозначности называется нормировкой.
|
- |
^Мш |
г |
|
На Земле сила, действующая на тело массой т, равна г - -О —; |
, |
а |
||
|
|
г1 |
г |
|
гЫг |
„ , , (\ |
1 |
|
|
работа при перемещении тела \р<Й = - ОМт\—- = -ОМт |
|
|
|
|
|
г\ |
г2 |
|
|
Космические скорости. |
|
|
|
|
Для того, чтобы тело стало спутником Земли, ему надо сообщить |
|
|
||
первую космическую скорость и\, которая |
находится |
из условия: |
||
дай,
Кз
9
отсюда Р] = ^/^7 ~ 7,91к м /.
Для преодоления силы притяжения Земли телу необходимо сообщить вто-
|
|
2 |
рую космическую скорость о2, которая находится из условия: |
|
— = т§К |
|
||
отсюда и2 = ^2%К3 * 11,2 ^. |
|
|
Чтобы тело могло покинуть пределы солнечной системы ему необходимо сообщить третью космическую скорость, которую можно найти из закона со-
|
то*2 |
|
тМг |
|
|
хранения энергии: |
|
= С |
|
-, где Мс |
- масса Солнца. |
|
|
||||
|
2 |
|
К3 |
|
|
Тема 7. Неинерциальные системы отсчета (НСО)
Неинерциальной системой отсчета называется система, движущаяся уско ренно относительно инерциальной. Простейшими НСО являются системы, движущиеся ускоренно прямолинейно, а также вращающиеся системы.
Силы инерции.
I закон Ньютона в НСО не имеет смысла, 111 закон Ньютона также утрачи вает ясное физическое содержание. Второй закон Ньютона формулируется без изменения, но наряду с силами взаимодействия необходимо учесть силы инерции.
Существование сил инерции обусловливается ускорением движения НСО относительно ИСО. В НСО второй закон Ньютона имеет вид: та' = Р + Рин, где а'- ускорение в НСО, Р- «обычные» силы как результат взаимодейст вия, Рин- силы инерции, которые равны:Рин = [а' - а)
Выражение для сил инерции в движущейся прямолинейно НСО имеет вид: Р'ин = т(®' ~ я) = -та0 или в векторной форме Рт = -та0, где а - абсолют ное ускорение относительно ИСО, а' - относительное ускорение в НСО, а0
- переносное ускорение. Сила инерции направлена противоположно перенос ному ускорению НСО.
Невесомость.
В свободно падающей НСО силы инерции полностью компенсируют дей ствие силы тяжести, наступает состояние невесомости. В состоянии невесо мости при свободном падении инертная и гравитационная массы тела равны. Инертная масса т характеризует инертные свойства тела, а гравитационная масса тг - силу, с которой тела притягиваются по закону Ньютона. На тело с гравитационной массой тг со стороны Земли с гравитационной массой Мг
10
действует |
сила |
Р = С — |
|
|
|
—. Сила |
тяжести Р = т§, отсюда ускорение |
|||
|
К2 |
|||||||||
|
|
|
|
|
|
|
|
|
||
р ОтгМг |
СМ г тг |
тг |
_ |
|||||||
$ = — = |
|
|
' — — = |
|
|
— = сот1 ——, где О- гравитационная постоян- |
||||
|
|
|
|
|||||||
т |
тК2 |
|
К2 |
т |
|
т |
||||
ная, К - радиус Земли. Так как ускорение § для всех тел у поверхности Земли одинаково, то инертная и гравитационная массы пропорциональны друг дру гу. Эксперименты показали, что эти массы равны друг другу с точностью до
-1? |
и г - т |
_„ |
|
10 их значений, т.е. |
— |
|
<10 . Благодаря тому, что тг = т, то при |
|
|||
|
тг |
|
|
свободном падении Рин |
= Р-р, т.е. компенсируют друг друга. |
||
Принцип эквивалентности.
Поле тяготения может меняться при переходе от одной точки пространст ва к другой. Нельзя подобрать систему отсчета, в которой ее ускорение в ка ждой точке пространства эквивалентно по своему действию с имеющимся там полем тяготения. Однако в достаточно малой области пространства после тяготения можно считать постоянным и воспользоваться принципом эквива лентности, которое гласит: в некоторой системе отсчета наличие ускорения ее неотличимо от присутствия соответствующего поля тяготения. Например, поле тяготения оказывает важное действие на свет - изменяет его частоту. Неизбежность изменения частоты света в поле тяготения следует из принципа эквивалентности.
Эффект уменьшения частоты света при распространении против силы тя жести называется красным смещением.
Центробежная и кориолисова силы инерции.
Сила инерции, связанная с переносным ускорением, называется центро бежной силой инерции: Рт =та2К .
Кориолисово ускорение в векторной форме ак =2ё-й', где со - угловая скорость вращения системы, о' - относительная скорость движения точки вдоль радиуса. Сила инерции Рк = -2тсЪ • и' называется силой Кориолиса.
Законы сохранения в НСО.
В НСО наряду с «обычными» силами действуют силы инерции. Эти силы всегда являются внешними по отношению к рассматриваемым телам. В НСО нет замкнутых систем материальных тел, следовательно нет законов сохране ния энергии, импульса и моментов импульса в обычном смысле.
Выход один - силы инерции необходимо включить в число сил системы и считать после этого систему замкнутой, для которой и в НСО будут выпол няться законы сохранения перечисленные выше.
п

Тема 8. Кинематика абсолютно твердого тела
Поступательное движение.
Движение твердого тела называется поступательным, если все его точки движутся по одинаковым траекториям. Скорости всех точек тела в любой момент времени одинаковы, углы Эйлера постоянны, число степеней свободы равно трем.
Плоское движение.
Плоским называется движение, при котором траектории всех точек лежат в параллельных плоскостях. Число степеней свободы равно трем. Масса сис темы материальных точек равна сумме масс покоя составляющих ее точек. Положение воображаемой точки, которую называют центром масс, задается
радиусом |
- вектором Я = — ^т0г{ . Скорость движения центра масс |
|
т |
,7 йЙ |
_ |
V = —, а его импульс р = тУ . За движением центра масс можно следить так
ш
же, как за движением материальной точки. Уравнение движения имеет вид:
(IV - т = Р.
Л
Вращательное движение.
Движение, при котором две точки тела остаются все время неподвижными, называется вращательным. Прямая, проведенная через эти точки называется осью вращения. Все точки твердого тела, лежащие на оси вращения, неподвиж ны. Остальные точки твердого тела движутся по окружностям в плоскостях, перпендикулярных оси вращения, а их центры лежат на оси вращения.
Степени свободы.
Число независимых параметров, которыми описывается движение систе мы материальных точек, называется числом ее степеней свободы. Матери альная точка имеет три степени свободы. Две точки жестко связанные между собор! имеют пять степеней свободы. Твердое тело имеет шесть степеней сво боды.
Углы Эйлера характеризуют взаимное расположение двух прямоугольных систем координат: (х',У',2') и (Х,У,2). Начало координат этих систем О' и О совпадают.
Плоскость X' У ' пересекает плоскость ХУ по линии Оц, называемый линией узлов. Узлы Эйлера 0 < ф < 2 я , 0 < Т < 2я, 0 < О < я, причем ср - угол собственного вращения, У - угол прецессии, © - угол нутации. Движение твердого тела описывается с помощью углов Эйлера.
Тема 9. Динамика абсолютно твердого тела
Бесконечно малое угловое перемещение йф материальной точки происхо дит в течение бесконечно малого промежутка времени. Поэтому угловая ско рость ё = — и направлена параллельно оси вращения. Линейная скорость и
точки направлена по касательной к траектории движения точки. Связь между
и и со имеет вид: V = со • г .
Угловое ускорение.
Производная угловой скорости по времени называется угловым ускорени-
ем: е = — .
Л
Ф В <&• Л
Уравнения движения.— = г , — = М Момент инерции.
Основное уравнение динамики вращательного движения твердого тела имеет вид: М = Ш, где М - момент сил, / - момент инерции тела, Е - угло вое ускорение. Момент инерции тела / = У] т1К1 .
(1 |
Т |
ху |
1 |
\ |
XX |
* |
1Х2 |
|
|
Совокупность величин ух |
УУ 1» |
называется тензором инерции. Ве |
||
гх 1.у 1»
личины 1ХХ, 1уу, 1^ называются осевыми моментами инерции, а 1ху = 1ух, /^ = 1и и 1уг = /гу центробежными моментами инерции.
Свободные оси.
Оси тела, совпадающие с осями координат, являются главными осями инерции, а величины 1Х = 1ХХ, 1У~ 1ууп1г = 1^ называются главными моментами инерции. Если главные оси проведены через центр масс тела, они называются центральными главными осями.
|
|
1 |
9 |
1 ( |
9 |
|
|
|
9 |
|
2 |
Кинетическая энергия вращения. Ек |
|
0 |
Ч—2х VI' |
е0 |
! |
+ |
^2 |
Ю |
2 + 1ъ |
ю |
|
=2— ти~и |
|
|
|
|
|||||||
1 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
При плоском движении Ек = — ти0 |
+—1со . |
|
|
|
|
|
|
|
|
||
Гироскопы.
Свободное вращение твердого тела возможно лишь вокруг центральных главных осей, их называют свободными. Аксиально-симметричное тело, при веденное в очень быстрое вращение вокруг своей оси симметрии, называется гироскопом. Ось вращения все время совпадает с осью симметрии гироскопа и момент импульса Ь = Ш. Прецессией называется движение оси гироскопа под действием внешнего момента сил, приложенных к ней. Нутацией называ ется движение оси тела вокруг полного момента импульса. Обычно вектор
12 |
13 |

момента импульса Ь = Ш всегда совпадает с центральной главной осью ги роскопа. Это совпадение обеспечивают гироскопические силы. К гироскопу
^ аЪ
удобно применить уравнение моментов — = М. Угловую скорость прецес-
ЛаЧ> М М
сии находим по формуле О = = — = —.
<М Ь 1со
Тема 10. Колебательное движение
Гармонические колебания.
Физические системы при малых отклонениях ведут себя как линейные ос цилляторы, их уравнение имеет вид: х + со0х = 0, где со0 = л]к/т - собствен
ная циклическая частота системы, к - жесткость, т - масса. Общее решение этого уравнения имеет вид: х = Асо5(со0С + а)
В комплексной форме х = Ае 1Ут1+а> Сложение гармонических колебаний.
а) Сложение колебаний одинакового направления.
|
|
|
|
|
X] |
= 0[ СОЗ (а 0( |
+ а ! ) |
|
|
|
|
|
|
|
|
х 2 = а 2 соз (со о ( + а 2 ) |
|
|
|
||
|
Амплитуда результирующего колебания |
|
|
|
|
|||||
|
Г~2 |
2 |
1 |
\ |
|
а\ 5ШСИ] |
+ а2 |
5та2 |
||
а = ^а\ |
+ а2 |
+ 2а^а2 соз(а2 |
~схх), начальная фаза 1§а - ау соза1 |
+ а2 |
соз«2 |
|||||
б) Сложение взаимноперпендикулярных колебаний |
|
|
|
|||||||
|
|
|
|
|
|
х = а сое со1 |
|
|
|
|
|
|
|
|
|
|
у = Ъ соз (со1 + а ) |
|
|
|
|
|
Уравнение |
результирующего |
колебания |
имеет |
вид: |
|||||
X2 |
V2 |
2ху |
. 2 |
|
|
|
|
|
||
Г+ — |
|
|
-С05а=51П а |
|
|
|
|
|
||
2 |
ъ1 |
аЬ |
|
|
|
|
|
|
||
а |
|
|
|
|
|
|
|
|
|
|
Нужно рассмотреть случаи, когда разность фаз а = 0, ± — , ± я .
Биения.
Особый интерес представляет случай, когда два складываемых гармони ческих колебания одинакового направления мало отличается по частоте. Та кое колебание называется биениями:
|
|
|
Х\ = а соз |
(о{ |
|
|
|
|
|
|
х2 = а соз (со о + А со )? |
|
|
|
|
Результирующее |
колебание |
описывается |
уравнением |
||||
х = 2асоз |
|
1 \со5со{, максимальная амплитуда колебания А = 2асоз |
|
1. |
|||
|
|
||||||
Затухающие колебания.
С учетом силы сопротивления среды, в которой происходят колебания, за-
. . . |
|
2 |
У |
пишем уравнение колеблющегося тела: х + 2/Зх + со$х = 0, где |
2/3 = — , |
||
7 к |
|
|
т |
|
|
|
|
«0 = —, где /3 - коэффициент затухания , г - коэффициент сопротивления |
|||
т |
|
|
|
среды. Решение уравнения имеет вид: х = «о6 сов(со( + а), со = ^со02 -/З2 |
|||
Логарифмический декремент затухания Я = 1п |
, |
ч = /37*, где Т - пери |
|
|
од + Т) |
|
|
од колебания.
Вынужденные колебания.
Колебания, которые возникают под действием внешней периодически из меняющейся силы, называются вынужденными. Пусть внешняя сила изменя ется со временем по гармоническому закону / = Р§ соз со I, тогда уравнение
•у
вынужденных колебаний будет иметь вид: х + 2Дх + ю0х = /о соз со 7, где /0 = —• Используя векторную диаграмму получим решение уравнение:
т |
|
|
|
|
|
|
|
|
2(Зсо |
|
|
|
|
|
|
|
|
с |
( со( - агс(§ |
|
|
|
|
|
/ о |
|
|
|
2 |
2 |
||
|
|
|
|
|
|
|
^ 2 |
|
||
2 |
- ш |
2 |
) |
2 |
+4/3 |
2 |
|
й ) 0 -СО |
|
|
(ш0 |
|
|
|
со |
|
|
|
Маятники а) маятник Максвелла представляет собой массивный диск, подвешенный
на нити. Нить намотана на ось диска по обе стороны от диска.
Сила натяжения нити Т = г—5-~.—•*, где К0 - радиус диска, /0- момент
1 + Цо7/0)
инерции всей системы.
б) математический - идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Для малых колебаний уравнение движения: ф +со0ср = 0, его решение
ср = асо&(со0( + а). Период колебания Т = 2п \—, где /- длина нити.
в) физический - это твердое тело, способное совершить колебания вокруг неподвижной точки, не совпадающей с его центром инерции. Уравнение для
2 |
2 |
"ЧГ^ |
|
малых колебаний ф + со0ср = 0, гдесо0 = |
|
,/-расстояние от точки подвеса |
|
|
|||
до центра масс, / - момент инерции маятника относительно оси, проходящей через точку подвеса.
14 |
15 |
|
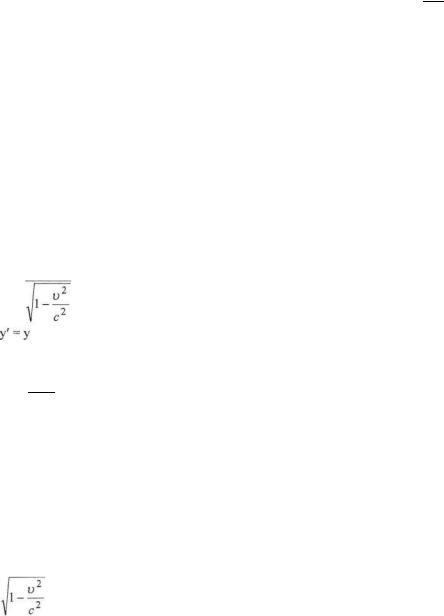
Период колебания Т = 2л прш |
, где 1прив - —. |
У § |
т1 |
Тема 11. Основы специальной теории относительности
Принцип относительности Эйнштейна - все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой.
Принцип постоянства скорости света - скорость света в вакууме одинако ва во всех инерциальных системах отсчета и не зависит от движения источ ников и приемников света.
Преобразования Лоренца Исходя из указанных выше принципов для двух ИСО (К- неподвижная, К'
- подвижная, движется со скоростью и относительно системы К) найден ко эффициент пропорциональности
"Й
Совокупность уравнений, которые называют преобразованиями Лоренца
|
х'+1)1' |
, |
х-01 |
имеют вид: |
х = , |
х = |
|
*-$
У = У'
2 = 2' |
|
|
2' = 2 |
|
|
|
|
, |
V |
, |
|
|
V |
|
|
Г + — Д С |
|
|
( |
„г |
гХ |
||
1= , |
2 |
|
{'= |
|
|
||
С |
|
с |
|
|
|||
|
2 |
|
|
|
2 |
|
|
|
с2 |
|
Ч |
|
|
с2 |
|
Следствия из преобразований Лоренца. |
|
|
|
|
|
||
а) Релятивистская масса |
т = |
| |
, при и -> с |
|
|
||
|
|
""7 |
|
|
|
|
|
т0 -масса покоя. |
|
|
|
|
|
|
|
б) Длительность событий в ИСО К и К': А( = - |
|
|
|
|
|||
в) Длина тела / = /0д/1 -, т.е. длина тела в направлении движения со
кращается.
Формулы преобразования скоростей при переходе от одной системы от счета к другой:
и,+и |
Ч1~7 |
"'Г? |
||
|
иу~~ |
|
|
|
1 + —г- 1 + —•— 1 + — г |
|
|||
с1 |
с1 |
с |
|
|
Релятивистское выражение для импульса р = тд = |
т |
|
||
|
|
|||
|
|
|
" |
* |
Релятивистское выражение для энергии Е = тс |
= ) |
|
-с , |
|
где Е0 = ШоС - энергия покоя частицы.
Тема 12. Деформации и напряжения в твердых телах
Под действием сил происходит деформация тел, т.е. изменение их разме ров и формы. Если после прекращения действия сил, вызвавших деформа цию, тело принимает первоначальные размеры и форму, деформация называ ется упругой. Если этого не происходит, то говорят об остаточной или пла стической деформации.
Основных видов упругих деформаций твердого тела два: растяжение (или сжатие) и сдвиг.
При растяжении или сжатии длина, например, стержня изменится на ве личину А/.
Относительное удлинение (или укорочение) стержня будет равно: е = — , где 10 - первоначальная длина стержня.
Р1 Р а
Нормальное напряжение о = —, тогда е = |
|
= —, где Е - модуль Юнга. |
||||
|
||||||
|
Е8 |
5 |
Е 8 |
Е |
||
По закону Гука Рупр = |
А/ |
= к • А/, где к- жесткость стержня. |
||||
|
||||||
Поперечные размеры стержня характеризуются относительным попереч-
, Ас!
ным расширением или сжатием: е = —, где а- первоначальный поперечный
с1
16 |
17 |

размер стержня, А с/ - изменение поперечных размеров стержня. Между е и е' существует связь: е' = ~ре, где \х - коэффициент Пуассона.
Сдвиг.
Возьмем тело в форме прямоугольного параллелепипеда, приложим к его противоположным граням равные, но противоположно направленные силы /] и / 2 . В любом сечении возникает тангенциальное (касательное) напряже-
ние г = —, под действием напряжения тело деформируется, верхняя грань
смещается относительно нижней на величину а, пусть ширина тела Ъ. Отно-
сительныи сдвиг у = — = (§ср, где ф - угол сдвига. Опыт показывает, что
Ъ
1 у = —т , где О - модуль сдвига, зависит от свойств материала.
О
Энергия упругих деформаций. Плотность энергии упругой деформации при сдвиге равна II = Су
Тема 13. Механика жидкостей и газов
Проведем в движущейся жидкости линии так, чтобы касательная к ним в каждой точке совпадала по направлению с вектором о , эти линии называют ся линиями тока. Часть жидкости, ограниченная линиями тока, называется трубкой тока. Пусть в трубке тока 0\ и и2 скорости течения жидкости в сече ниях 5*1 и 5г. Объемы жидкости в сечениях, протекающие за единицу времени через сечения ^ и 52 должны быть одинаковы: §г^1 = 82^2 Следовательно, для несжимаемой жидкости величина 8-и = сот1 - теорема о неразрывности струи.
Закон Бернулли.
В стационарно текущей идеальной жидкости вдоль любой линии тока вы-
полняется условие |
|
+ р§п + р = сот1. |
|
Закон Стокса.
Сила сопротивления движению шарика в жидкостях при небольших ско ростях равна: Р= блцги, где г - радиус металлического шарика, движущегося в жидкости, г] - динамическая вязкость жидкости.
Поток жидкости через трубу радиусом К вычисляется по формуле Пуазей-
(р, - р?)кК4
ля: (2 = -^ |
|
, где рхк рг- давления жидкости на входе и выходе тру- |
|
Щ • I |
|||
|
|
||
бы,/-длина трубы. |
|
||
Различают два вида течения жидкости (или газа): ламинарное и турбу лентное. Ламинарное течение стационарно, частицы жидкости не переходят из одного слоя в другой. Турбулентное течение не стационарно, вихревое, частицы жидкости в слоях перемешиваются.
Характер течения определяется числом Рейнольдса: Ке = ро1 , где р -
плотность жидкости (или газа), и - средняя (по сечению трубы) скорость по тока, / - размер поперечного сечения устройства, по которому течет жидкость.
Если Ке < 10 , то течение ламинарное. Подъемная сила.
При движении тела в жидкости на него действуют две силы: сила лобового сопротивления ^ и подъемная сила Р. Лобовое сопротивление складывается из сопротивления трения и сопротивления давления. Наименьшим сопротивлением давления обладают тела хорошо обтекаемой каплевидной формы.
Силой, поддерживающей, например, самолет в воздухе, служит подъем ная сила, действующая на его крылья. Чтобы увеличить подъемную силу Р и уменьшить силу лобового сопротивления <2 крыльям самолета и его фюзеля жу придают хорошо обтекаемую форму.
В развитии аэродинамики большая заслуга великого русского ученого Н.Е. Жуковского и его ученика С.А. Чаплыгина.
Тема 14. Волны в сплошной среде и элементы акустики
Процесс распространения колебаний в упругой среде называется волной. Частицы среды, в которой распространяется волна, не переносятся волной, они лишь совершают колебания около своих положений равновесия
В продольной волне частицы среды колеблются вдоль направления рас пространения волны. В поперечной волне частицы среды колеблются в на правлениях, перпендикулярных к направлению распространения волны.
д2^ |
д2$ |
д2^ |
1 д2^ |
|||||
Волновое уравнение. — - н |
|
|
- + —- = — |
|
|
—, где с - смещение колеб- |
||
|
|
|
|
|||||
дх2 |
ду2 |
дг2 |
и2 |
д(2 |
||||
лющейся частицы от положения равновесия, о - скорость распространения волны.
Вектор |
плотности потока энергии (вектор |
Умова) ] = йи, где |
|
- 1 |
2 |
2 |
. |
и = — ра |
со |
- среднее значение плотности энергии, |
и - фазовая скорость |
волны. |
|
|
|
Тогда ]ср |
= йи =—ра2ю26, гдерплотность среды, а - амплитуда волны. |
||
Интерференция и дифракция волн. |
|
||
