КР_Заоч_3курс_Цифровая обработка сигналов

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ

Кафедра общей теории связи

Контрольная работа

по дисциплине

Цифровая обработка сигналов

Выполнил:

Студент гр. БСС1952

Проверил:

Ассистент

Кудряшова Анастасия Юрьевна

Москва, 2021

Вариант 05

Задание 1.

Цифровой фильтр (ЦФ) второго порядка задан своими параметрами:

а) коэффициентами числителя передаточной функции b₀ = 0,9, b₁ = 2,8, b₂ = 0,1;

в) коэффициентами знаменателя передаточной функции a₁ = -1,1, a₂ = -0,8.

Требуется:

1. Записать разностное уравнение ЦФ.

2. Изобразить структурную каноническую схему ЦФ.

3. Рассчитать 20 значений импульсной реакции ЦФ и построить в масштабе её временную диаграмму.

4. Рассчитать 20 значений переходной функции ЦФ и построить в масштабе её временную диаграмму.

5. Записать выражение для передаточной функции ЦФ и получить выражения для амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристик ЦФ.

6. Рассчитать по 20 значений АЧХ и ФЧХ ЦФ для дискретных значений частот f_i = i/19Т, где i = 0, 1, 2, ..., 19, где T = 125 мкс – интервал дискретизации.

Построить в масштабе графики АЧХ и ФЧХ ЦФ.

7. Рассчитать нули и полюса передаточной функции ЦФ. Определить, является ли заданный ЦФ устойчивым.

Решение.

1. Цифровой фильтр второго порядка описывается разностным уравнением:

y_i = a₁y_i-1 + a₂y_i-2 + b₀x_i + b₁x_i-1 + b₂x_i-2 = –1,1 y_i-1 – 0,8 y_i-2 + 0,9 x_i + 2,8 x_i-1 + 0,1 x_i-2,

где i = 0, 1, 2, …, 19; y_-1 = y_-2 = x_-1 = x_-2 = 0.

2. Структурная каноническая схема ЦФ показана на рис. 1.

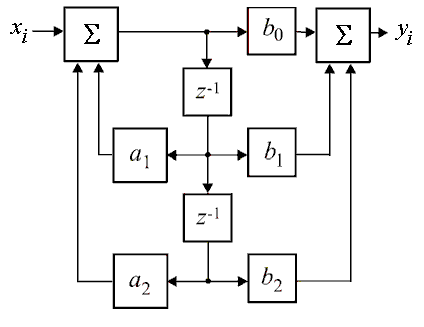
Рис. 1. Структурная каноническая схема ЦФ второго порядка.

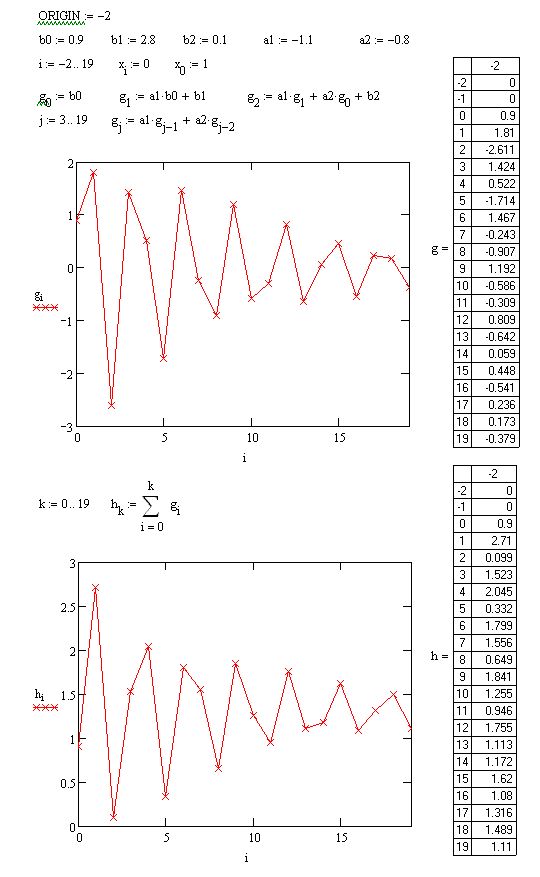
3. В соответствии с разностным уравнением (п.1) импульсная реакция ЦФ определяется как g_i = y_i при единичном входном сигнале: x₀ = 1, x_i = 0 при i ≠ 0.

g₀ = b₀, i = 0,

g₁ = a₁b₀ + b₁, i = 1,

g₂ = a₁g₁ + a₂g₀ + b₂, i = 2,

g_i = a₁g_i-1 + a₂g_i-2, i ≥ 3.

4. Переходная функция связана с импульсной реакцией ЦФ следующим соотношением:

, k = 0, 1, 2, …, 19.

Таблицы значений g_i и h_i, временные диаграммы импульсной реакции и переходной функции, рассчитанные в программе MathCad v.13.0, представлены в Приложении.

5. Передаточная функция исследуемого ЦФ задается соотношением

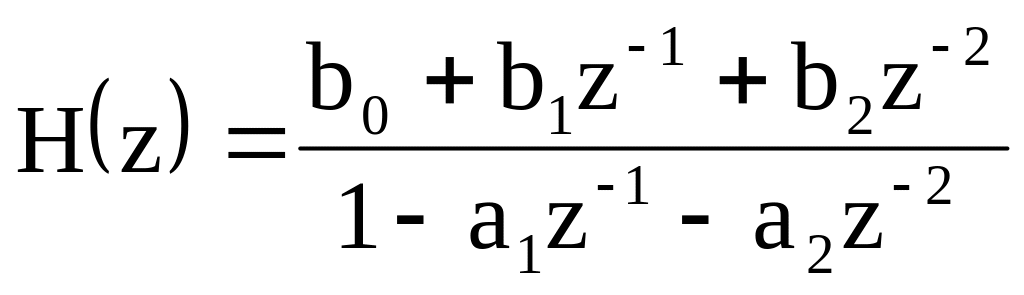
Для определения АЧХ и ФЧХ ЦФ в передаточной функции вначале следует сделаем подстановку z = е^jωT = cos(ωT) + j*sin(ωT) и найдем действительные и мнимые части числителя и знаменателя функции H(z). В результате имеем

z^–1 = е^–jωT = cos(ωT) – j*sin(ωT)

z^–2 = е^–2jωT = cos(2ωT) – j*sin(2ωT)

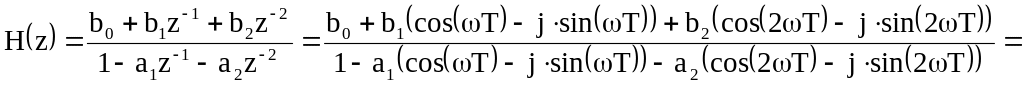
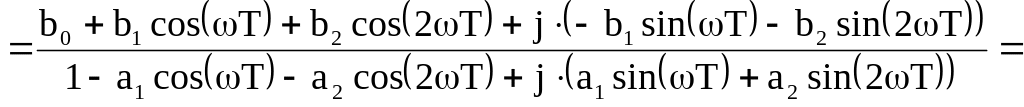
Здесь искомые функции соответственно равны:

действительная часть числителя

Re K₁(jω) = R₁(ω) = b₀ + b₁*cos(ωT) + b₂*cos(2ωT),

мнимая часть числителя

Im K₁(jω) = I₁(ω) = –b₁*sin(ωT) – b₂*sin(2ωT),

действительная часть знаменателя

Re K₂(jω) = R₂(ω) = 1 – a₁*cos(ωT) – a₂*cos(2ωT),

мнимая часть знаменателя

Im K₂(jω) = I₂(ω) = a₁*sin(ωT) + a₂*sin(2ωT),

С учетом полученных выражений и введенных обозначений, находим:

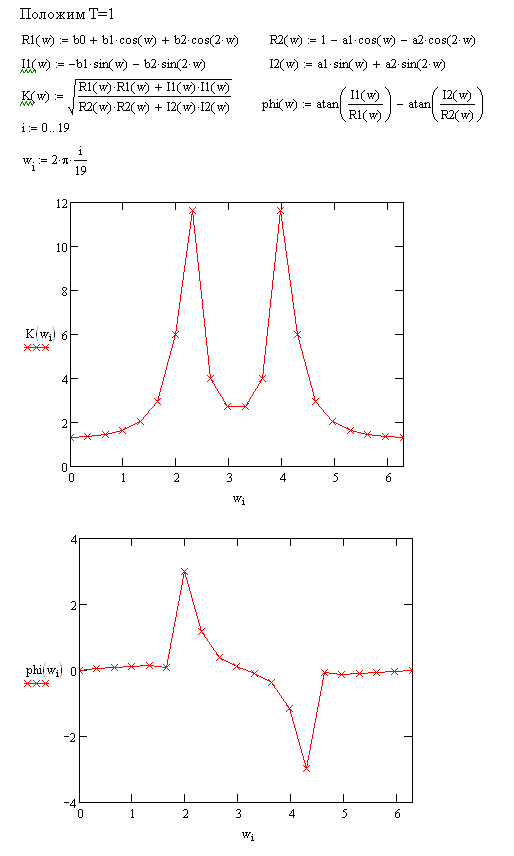
амплитудно-частотная характеристика (АЧХ) ЦФ

K(ω) = ([R₁²(ω) + I₁²(ω)]/[R₂²(ω) + I₂²(ω)])^1/2,

фазо-частотная характеристика (ФЧХ) ЦФ

φ(ω) = arctg[I₁(ω)/R₁(ω)] – arctg[I₂(ω)/R₂(ω)].

6. Для построения графиков АЧХ и ФЧХ ЦФ их дискретные значения

K_i = K(ω_i) и φ_i = φ(ω_i) рассчитываются на дискретных частотах

ω_i = 2πf_i, f_i = i/19T = if_d/19, i = 0, 1, 2, ..., 19, где f_d – частота дискретизации.

Таблицы значений K_i и φ_i, графики АЧХ и ФЧХ ЦФ, рассчитанные в программе MathCad v.13.0, представлены в Приложении.

7. Нули Z₀₁ и Z₀₂ передаточной функции находятся как корни уравнения:

b₀z² + b₁z + b₂ = 0.

Полюса Z_p1 и Z_p2 передаточной функции находятся как корни уравнения:

z² – a₁z – a₂ = 0.

С помощью системы MathCad v.13 (см. Приложение) находим нули передаточной функции: Z₀₁ = -3,075, Z₀₂ = -0,036 и ее полюса: Z_p1,2 = -0,55 ± j*0,705.

|Z_p1| = |Z_p2| = 0,894 < 1, следовательно, ЦФ устойчив.

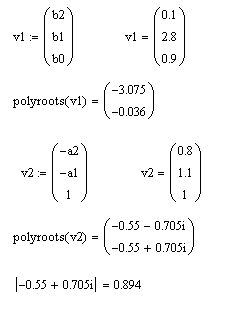
СПИСОК ЛИТЕРАТУРЫ

1. Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка сигналов: Учеб. пособие для вузов. - 2-изд., перераб. и доп. - М.: Радио и связь, 1990.

2. Стеценко О.А. Радиотехнические цепи и сигналы: Учебник. - М.: Высш. шк.,2007.

3. Солонина А.И., Улахович Д.А., Арбузов С.М., Соловьева Е.Б. Основы цифровой обработки сигналов. - 2-изд. – Санкт-Петербург.: «БХВ- Петербург», 2005.

9