Ответы к ГОСу / Новая папка / 1

1. Матрицы. Определение, умножение матриц на число и сложение их, умножение матриц, ранг матрицы и его нахождение путем элементарных преобразований, вычисление обратной матрицы по формулам и методом исключения.

Матрицы – это прямоугольные таблицы элементов из m строк и n строк.

m, n – порядки матрицы, они определяют размерность матрицы

Обозначение:

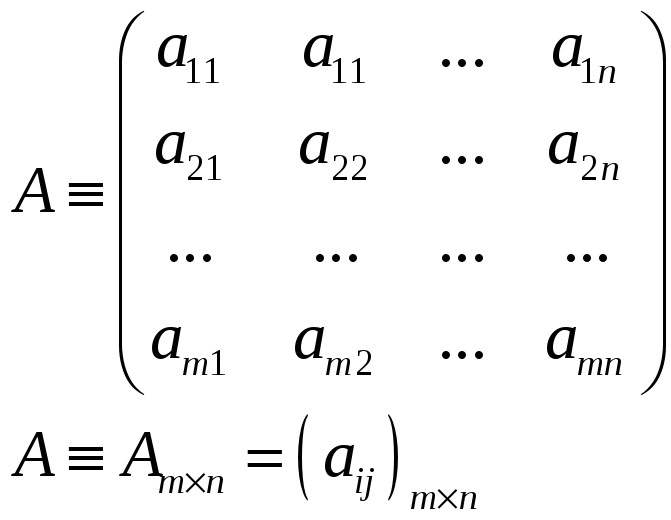
Если m = n, то матрица называется квадратной. В случае квадратной матрицы вводятся понятия главной и побочной диагонали матрицы (главная: i = j; побочная: i = n - j + 1).

[Равенство двух матриц] A = B, если

1) dim A = dim B

2)

Основные операции над матрицами:

1. Пусть dim A = dim B (необходимое условие), тогда суммой матриц А и В называется новая матрица С_mn: с_ij=a_ij+b_ij . (1)

Обозначение:

Операция получения суммы называется сложением.

Свойства операции сложения:

1 А+В=В+А (коммутативность)

2 (А+В)+С = А+(В+С) (ассоциативность)

Док-во очевидным образом из определения.

2. Произведение матрицы А на число R называется матрица С: c_ij = a_ij (2)

Обозначение: (по определению, доказывать не надо)

Свойства:

1 ()А = (А) (ассоциативность)

2 (А+В) = А+В (дистрибутивность относительно сложения матриц)

3 (+)А = А+А (дистрибутивность относительно сложения чисел)

Док-во из определения, расписываются левые и правые части и сравниваются.

ЗАМ: Разностью матриц А и В называется матрица С: С + В = А. Обозначение . Имеет место:

3. Умножение матрицы на матрицу (перемножение матриц)

Произведением матрицы А_mn на матрицу В_np называется матрица С_mp: (3)

Обозначение:

(Строка i матрицы А умножается на столбец j матрицы В в смысле скалярного произведения)

Свойства:

1 (АВ)С=А(ВС) (ассоциативность)

2 А(В+С) = АВ+АС

(А+В)С = АС+ВС (дистрибутивность)

Док-во через сравнение размерностей прав и лев частей. Докажем 2:

ЗАМ: Произведения АВ и ВА определены и имеют одну и туже размерность лишь тогда, когда, А и В – квадратные матрицы одного и того же порядка. Для таких матриц можно исследовать коммутативность. Вообще говоря, коммутативность не выполняется АВВА. Можно показать на простых примерах. Имеются некоторые частные случаи, когда коммутативность выполняется:

Если D = D_n – диагональная матрица, то

В частности если D = E и D = 0.

Ранг матрицы – max порядок отличных от 0 миноров r(A)=rang(A).

Из Т. о базисном миноре следует, что ранг матрицы есть max число линейно независимых строк или столбцов. Находят ранг несколькими способами:

1. методом элементарных преобразований. Используют тот факт, что элементарные преобразования матрицы не меняют ее ранг. Элементарные преобразования:

• перестановка любых двух строк (столбцов)

• умножение любой строки (столбца) на любое число, не равного 0

• умножение любой строки (столбца) на любое число и прибавление полученного результата к любой строке (столбцу)

Используя элементарные преобразования, приводят матрицу к треугольному виду, более того можно привести к диагональному виду.

2. метод окаймляющих миноров. Пусть в матрице найден , тогда рассматривают лишь те миноры (k + 1) порядка, которые содержат в себе .

Если все такие миноры = 0, то r(A) = k. Если же среди них , то процесс повторяется.

Обратная матрица.

A = (А_nn)

Матрица В называется правой обратной к А, если АВ = Е

Матрица C называется левой обратной к А, если СА = Е.

Если В и С существует, то В = С.

Если А – невырожденная (), то вместо «левой» и «правой» говорят просто об обратной матрице к А. Таким образом, обратная матрица В определяется отношением:

АВ = ВА = Е.

Из этого равенства видно, что А и В взаимообратные, А = В^-1 и В = А^-1

Нахождение обратной матрицы

1. По формулам:

Вычисляется det A,

Если det A0, то вычисляется P=P_A (А_ij – алгебраическое дополнение),

В=Р^Т,

.

2. Метод исключения (на основе метода Гаусса)

Образуем систему линейных уравнений , (1)

АХ=У. (2)

X – неизвестные

Y – условно считаются известными.

По теореме Крамера система имеет единственное решение (так как )

Для построения обратной матрицы систему (2) решаем методом Гаусса, т.е. методом последовательного исключения:

,

Х=ВУ,

С другой стороны, с учетом (2) Х= А^-1У. Так как решение единственно, то В= А^-1.