Ответы к ГОСу / Новая папка / 29

29. Модель оптимального поведения потребителей на рынке товаров в условиях товарно-денежных отношений.

В основе модели лежит гипотеза о том, что потребители при заданных ценах на товары и заданном доходе стараются максимизировать уровень удовлетворения своих потребностей при выборе товара.

Исследуется поведение некоторой группы потребителей на рынке, на котором представлены n товаров, которые будем обозначать:

y = (y₁ … y_n) – набор товаров / услуг

р = (р₁ … р_n) – заданные цены на товары / услуги.

u(y) – целевая функция потребления. Представляет собой критерий. Для ее построения нужны маркетинговые исследования. Она отвечает на вопрос, что такое хорошо и плохо для потребителя, т.е. определяет предпочтения потребителя

D – доход потребителя, может представляться как средний доход для изучаемой группы потребителей.

Тогда задача имеет вид:

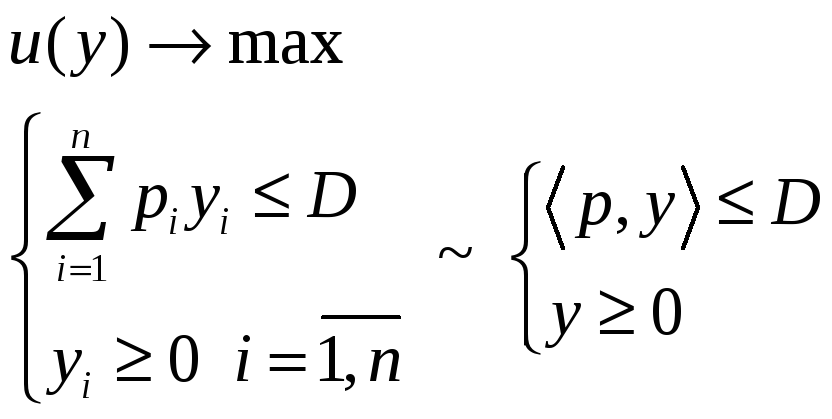
Графическая интерпретация для случая двух товаров:

Линии уровня имеют такой вид, так как чем больше потребитель потребляет товар, тем менее предпочтительным он становится

Присутствующий в модели принцип оптимального поведения потребителей естественно не стоит понимать, как будто потребитель перед покупкой делает вычисления на основании свойств товаров.

Эта модель предназначена для выявления тенденции поведения потребителей.

В эту модель добавляют ограничения на объем производства, так как он может быть выше спрос. Особым моментом модели является учет денежных сбережений. Существует 2 способа решения проблемы:

1. денежные сбережения рассматриваются как особое потребительское благо, которое имеет свою общественную полезность.

2. Предполагается, что имеется возможность заранее оценить величину сбережений. Тогда величина дохода D рассматривается в модели как некоторая часть сбережений, которую потребитель готов потратить.

Для исследования свойств модели (1)-(3) используется метод множителей Лагранжа.

1.

Обозначим , где

. Тогда получим:

2.

Если – товар потребляется, то , тогда

Из данного соотношения следует, что для потребляемых товаров отношения предельных (общественных) полезностей к ценам должны быть одинаковыми.

если k,l: , то

данное равенство показывает, что для максимизации уровня своего потребления потребитель может выбирать товары так, чтобы отношение предельных полезностей совпадало с уровнем цен.

3.

если , то

То есть для достижения максимального удовлетворения необходимо потратить весь запас денежных средств.

Основными направлениями использования модели являются

1. прогнозирование покупательского спроса в зависимости от цен и доходов,

2. регулирование цен и доходов для сбалансированности спроса и предложения.

Возможна следующая постановка вопроса: известен некоторый набор товаров у₀, которые могут быть реализованы. Требуется установить такие цены и общественный доход, чтобы спрос потребителей соответствовал товарному предложению. Опираясь на выведенные условия оптимальности:

.

Если

Опираясь на условия оптимальности, сформулируем задачу нахождения значения цен и дохода, балансирующих спрос и предложение:

, i = 1,n₁ (n₁-число реализуемых продуктов).

Система включает (n₁+1) уравнение, (n₁+2) переменные: р_i – цены, D – доход, – множ-ль Лагранжа.

Если зафиксировать 1 из этих переменных, то получим одинаковое количество и уравнений, и неизвестных = (n₁+1), т.е. система уравнений разрешима.