Ответы к ГОСу / 27

27. Типичные производственные функции с несколькими ресурсами: линейная ПФ, степенная ПФ, ПФ с постоянными пропорциями. Коэффициенты эффективности использования ресурсов для этих типов функций.

Производственные возможности н/х в любой момент времени определяются 2-мя группами факторов:

1. технологические условия производства, которые выражают зависимости между затратами разных ресурсов и выпуском продукции

2. объем и качество используемых ресурсов

f(x) – производственная функция, зависимость результата производства (объема выпуска продукции) от затрат ресурсов.

X = (х₁, …, х_m) – вектор затрат ресурсов.

ПФ характеризует максимально возможный выпуск продукции при определенных затратах ресурсов. Объемы выпуска продукции являются максимальными в том смысле, что при данных затратах ресурсов невозможно увеличить объем выпуска одного продукта, не уменьшив при этом выпуск другого продукта.

Построение такой функции является сложной проблемой, поэтому на практике применяют отдельные частные виды ПФ.

Наличие многоассортиментных технологических процессов не позволяет описать множество производственных возможностей н/х, но не препятствует описанию однопродуктовых производственных процессов.

Существует два основных подхода для построения ПФ:

1) статистический. ПФ строится на основании наблюдений о соотношении затрат и выпуска продукции.

2) оптимизационный. Параметры ПФ определяются в результате обобщения решения оптимизационных задач при изменяющихся параметрах.

С точки зрения ресурсов различают ПФ с взаимозаменяемыми и взаимодополняемыми ресурсами. Взаимозаменяемость предполагает, что один и тот же объем выпуска продукции может быть получен при разных комбинациях объемов ресурсов.

Изокванты – линии уровня производственной функции.

Показатели:

1. Средняя эффективность – показывает отдачу от каждой единицы i-го ресурса;

2. Предельная эффективность – показывает предельный прирост выпуска продукции при увеличении затрат i-го ресурса на малую величину. – только для взаимозаменяемых ресурсов;

3. Эластичность производства 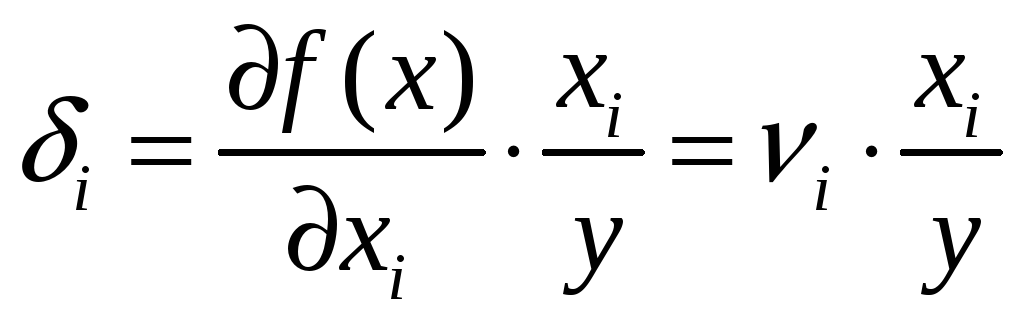– отражает отношение относительного прироста продукции к относительному приросту i-го ресурса;

Норма эквивалентной взаимозаменяемости ресурсов – показывает, какое количество i-го ресурса может быть высвобождено из производства при увеличении затрат j-го ресурса на 1;
Коэффициент эластичности взаимозаменяемости ресурсов	– показывает, на сколько % должно измениться отношение объемных затрат ресурсов i и j, чтобы при этом норма эквивалентной заменяемости изменилась на 1%.

1. Линейная производственная функция:

	В соответствии с этой формулой имеет место постоянная отдача от увеличения масштабов производства. Изобразим на графике поведение функции. На уровне x2 прирост x1 будет давать один и тот же прирост производства, т.е.

2. Степенная производственная функция:

При фиксированном выпуске продукции предельная эффективность i-го ресурса падает с ростом затрат на него.

Норма взаимозаменяемости растет с ростом удельных затрат j-го ресурса, т.е. для компенсации одной единицы продукции i-го ресурса требуется все большее количество затрат j-го ресурса. При изменении нормы эквивалентной взаимозаменяемости на 1% соотношение продуктов также должно измениться на 1%. Эластичность взаимозаменяемости равна 1, что является недостатком модели, так как согласно статистическим исследованиям такого быть не должно. Рассмотрим, каким образом темп роста производства зависит от темпов роста затрат ресурсов: Темп роста объемов производства линейно зависит от темпов роста затрат ресурсов: Если объем затрат ресурсов изменился на 1% для каждого ресурса, то объем выпуска продукции изменится на . Во многих случаях для выполняется условие для них объем выпуска изменится на .

Степенная функция является разновидностью функции Кобба-Дугласа:

L – затраты труда,

K – затраты капитала, тогда

где

Функция предложена в 1920 году.

Изокванты степенной функции имеют асимптоты в виде осей координат, они не пересекаются для разных объемов производства.

Недостаток модели: 1) в каком бы очень маленьком количестве мы не имели ресурс, его всегда можно заменить достаточно большим количеством других ресурсов. 2) также равенство эластичности взаимозаменяемости 1. Поэтому ведутся разработки по избавлению от этого недостатка. Например, создаются функции с постоянной эластичностью замены, не равной 1.

3. Производственная функция с постоянными пропорциями:

– нормирующие множители:

– количество i-го ресурса, необходимого для выпуска продукции в размере .

Пусть (1)

Построим изокванты этой функции для

а) допустим в (1) min достигается при

Будем изменять затраты труда в большую сторону, тогда:

б) предположим

тогда

Функция с постоянными пропорциями является непрерывной, но недифференцируемой. Увеличение затрат одного ресурса при фиксированном значении второго не приводит к увеличению продукции, так как ресурсы взаимодополняемы. Поэтому эластичность взаимозаменяемости

Предельную эффективность каждого ресурса вычислить не можем, так как его нельзя рассматривать обособленно от других ресурсов.

Рассмотренные три типа ПФ являются базовыми, в чистом виде они не применимы. Но они описывают типичные производства. Помимо этих ПФ имеются некоторые модифицированные ПФ:

– начальные уровни запуска производства. Т.е. для запуска производства нужен определенный начальный уровень ресурсов

Ресурсы заменяют друг друга лишь до определенного момента. Например, серый хлеб: надо сохранять определенные пропорции.

Функция нелинейная, но отражает полностью взаимозаменяемые ресурсы