Ответы к ГОСу / 3

3. Системы линейных алгебраических уравнений. Условие существования решения, решение систем по формулам Крамера и методом исключений, фундаментальная система решений.

СЛАУ называется система n-го порядка: (1)

СЛАУ можно представить в виде матрицы АХ = В,

где

– известные коэффициенты системы (1)

– известные правые части системы (1)

– неизвестные (искомые) величины

• Набор (n-мерный набор) называется решением СЛАУ, если при подстановке их вместо соответствующих неизвестных 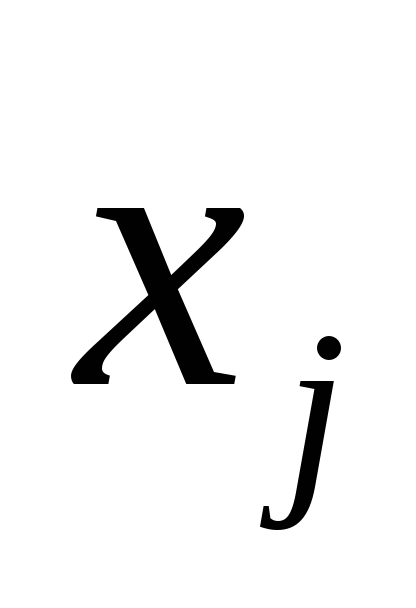каждое из уравнений системы превращается в истинное равенство (набор удовлетворяет (1)).

• Если система обладает хотя бы 1 решением, она называется совместной.

• Если имеется лишь единственное решение, то она называется определенной.

• Если имеется более 1 решения, то система называется неопределенной.

• Если нет ни одного решения, то она называется несовместной.

• Если решение одной системы является решением другой системы, то системы называются равносильными.

А – основная матрица

– расширенная матрица

Условия совместимости:

Т. Кронекера-Капелли. Система совместна (имеет хотя бы 1 реш-е) 

Док-во: ()

 решение (2)

А имеет базисный минор r-го порядка. Любой столбец А представляется в виде линейной комбинации базисных столбцов. Перепишем соотношение (2) в виде:

–

линейная комбинация r базисных столбцов максимальное число линейно независимых столбцов . Аналогично в обратную сторону.

Решение по формулам Крамера.

Метод применяется в случае квадратной СЛАУ:

Если определитель , то система n-го порядка имеет единственное решение, которое дается в формуле Крамера (в терминах элементов):

,

– определитель, полученный из основного путем замены j-го столбца столбцом из правой части В.

Док-во:

(для n = 3) Умножим на и складываем правые и левые части:

Аналогично для .

=>  A^-1 => X=A^-1B – формула Крамера в терминах матричного представления.

Метод Гаусса (метод последовательных исключения).

Не обязательно det0, не обязательно квадратные матрицы. Расширенную матрицу приводим к треугольному виду с единицами на главной диагонали путем элементарных преобразований строк (не столбцов). Элементарные преобразования – 1) перестановка любых двух строк (столбцов); 2) умножение любой строки (столбца) на любое число, не равного 0; 3) умножение любой строки (столбца) на любое число и прибавление полученного результата к любой строке (столбцу).

На каждом этапе исключаются некоторые переменные (отсюда название метода).

И потом обратный ход: с конца подставляем решение в предыдущую строку.

Пример

– «укороченная» система

Фундаментальная система решения однородной системы.

(2)

АХ=0

, т.к. В = 0. => (2) всегда имеет решение, т.е. совместна по теореме Кронекера-Капелли.

Если r = n => существует единственное нулевое решение по теореме Крамера, так как все .

Если r < n => k = n-r – число свобод неизвестных.

Множество решений системы (2) образует подпространство пространства R_n:

– ВП, поэтому (аксиомы проверять не надо) надо проверить лишь:

L – ВП, его размерность = k => достаточно найти k линейно независимых частных решений, т.е. фундаментальную систему решения.

ФСР является базисом подмножества решений однородной системы (2)

Если – базис, то общее решение есть линейная комбинация этих (свободных) элементов: .

ФСР показывает применение понятия базиса в теории СЛАУ.

Пр. r=2, k=4-2=2.

Исходная система ~

1. x₃=1, x₄=0 => x₁=0, x2=1 => f₁ = (0,1,1,0). 2. x₃=0, x₄=1 => x₁=0, x₂=-1 => f₂ = (0,-1,0,1).

f₁ и f₂ независимы, т.к. det0, существует минор II порядка отличный от 0.

{f₁, f₂} – базис или фундаментальная система решений. Общее решение: