25. Методы наискорейшего и координатного спуска для минимизации выпуклой функции без ограничений. Их алгоритмы и геометрическая интерпретация.

Выпуклой функцией на выпуклом множестве X называется функция: f(x₁ + (1 – )x₂)  f(x₁)+ (1 – )f(x₂)  x₁, x₂ X, [0,1]

Если в точке x₀ у выпуклой функции f локальный min, то в этой точке grad f = 0.

У выпуклой функции локальный min совпадает с глобальным.

Общих методов решения нелинейной задачи не существует, однако для некоторых классов нелинейных задач разработаны общие методы, в частности, когда функция является выпуклой. Тогда задача заключается в минимизации выпуклой дифференцируемой функции f(x), то есть

f(x)  min

Все методы спуска решения задачи безусловной минимизации различаются либо выбором направления спуска, либо способом движения вдоль направления спуска.

Решается задача минимизации функции f(x) на всём пространстве R_n. Методы спуска состоят в следующей процедуре построения последовательности {X_k}. В качестве начального приближения выбирается любая точка X₀R_n. Последовательные приближения X₁, X₂, … строятся по следующей схеме:

1. в точке X_k выбирают направление спуска –S_k – n-мерный вектор;

2. находят (k+1)-е приближение по формуле X_k+1 = X_k – _kS_k.

Направление S_k и параметр _k выбираются из условия сходимости последовательности решений к некоторому оптимальному решению X*, то есть необходимо обеспечить неравенство f(X_k+1) < f(X_k).

Вообще говоря, можно бесконечно долго приближаться к X*. В некоторых случаях мы можем попасть в точку X*, в которой grad f = 0. Поэтому решение задачи часто находиться с точностью до некоторого  или .

| X_k+1 – X_k| < 

| f(X_k+1) – f(X_k)| < .

Метод наискорейшего спуска

Если функция дифференцируема, то можно использовать градиентные методы. МНС является одним из вариантов градиентного спуска. Суть градиентного метода заключается в следующем: выбрать произвольную точку X₀ и с помощью антиградиента -f(X₀), вычисленного в этой точке, определить направление наискорейшего убывания функции и сместиться из точки X₀ по этому направлению:

Таким образом, строится последовательность {X_k}.

Если величину _k выбирать так, чтобы значение f = f(X_k+1) – f(X_k) было наименьшим, то градиентный метод называется МНС. В силу того, что f(X_k) известно и учитывая, что X_k+1=X_k –_kf(X_k), получаем, что приращение f является функцией одной переменной _k, то есть f = f (_k).

Согласно необходимому условию ext функции одной переменной должно выполняться:

Величину _k , при которой достигается наименьшее значение f , можно определить одним из методов одномерной минимизации.

Поиск решения прекращается, когда | X_k+1 – X_k| <  или | f(X_k+1) – f(X_k)| < .

Алгоритм метода наискорейшего спуска:

0 шаг. Выберем .

1 шаг. Находим . Если , то остановка и Х_k – решение.

2 шаг. Находится .

3 шаг. .

4 шаг. Если | X_k+1 – X_k| <  или | f(X_k+1) – f(X_k)| < , то остановка и Х_k+1 – решение

5 шаг. k=k+1, переход к шагу 1.

С геометрической точки зрения градиент в очередной точке X_k+1 ортогонален градиенту в предыдущей точке X_k. Для случая функции двух переменных МНС имеет следующую геометрическую интерпретацию: для любого к луч, идущий от точки X_k к точке X_k+1, перпендикулярен к линии уровня функции, проходящей через точку X_k, и касается линии уровня, проходящей через точку X_k+1.

Метод покоординатного спуска

Одним из наиболее простых способов определения направления спуска является выбор в качестве S_k одного из координатных векторов e₁, e₂, …, e_n, вследствие чего у X_k на каждой итерации изменяется лишь одна из компонент. Существуют многочисленные варианты покоординатного спуска. Рассмотрим 2 из них.

Обозначим через e_i =(0..0, 1, 0..0) – вектор, у которого на i-ой позиции находится 1.

Поиск решения прекращается, когда _k < .

Метод ПС может применять (не всегда эффективно) и для не дифференцируемых функций, так как сам алгоритм покоординатного спуска не требует вычисления производной функции.

Теорема [о сходимости МПС]. Пусть функция f(x) является выпуклой в R_n и имеет непрерывную производную. Тогда последовательность точек МПС сходится к точке min.

Алгоритм метода покоординатного спуска:

0 шаг. Выберем .

1 шаг. Положим:

(1)

Условие (1) обеспечивает перебор координатных векторов.

2 шаг. Вычисляют значение целевой функции f(X) в точке и проверяют неравенство:

(2)

Если (2) выполняется, то полагают:

Проверяется условие прекращения решения и при необходимости переход к шагу 1.

3 шаг. Если (2) не выполняется, то вычисляют значение целевой функции f(X) в точке и проверяют неравенство:

(3)

Если (3) выполняется, то полагают:

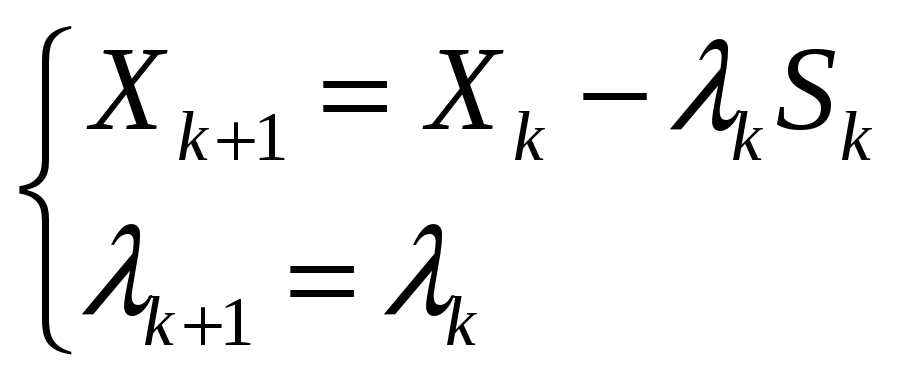
Проверяется условие прекращения решения и при необходимости переход к шагу 1.

4 шаг. (k+1)-ая итерация называется удачной, если справедливо либо (2), либо (3), иначе она является неудачной и шаг _k дробиться / увеличивается.

Существует другой вариант ПС, основанный на использовании градиента функции.

Поиск решения прекращается, когда | X_k+1-X_k| <  или .

Алгоритм метода покоординатного спуска:

0 шаг. Выберем .

1 шаг. Находят максимальный по абсолютной величине из частных производных (элементов градиента), вычисленных в точке X_k, то есть

Обозначим через i_max номер элемента, соответствующего S. Тогда координатный вектор

В качестве S_k выбирается

S_k = e_kS, если частная производная отрицательна, и

S_k = -e_kS, если частная производная положительна.

2 шаг. Находится

3 шаг.

4 шаг. Проверяется условие прекращения решения.