
Мальханов - Общая Физика
.pdfО ПРЕДМЕТЕ ФИЗИКИ
Человеку неизвестны окончательные истины, а известно только то, что можно сказать об излагаемом предмете, исходя из современного уровня науки.
Физики изучают явления, происходящие в неживой природе. На основе опытов и размышлений создаются модели явлений. Эти модели изменяются со временем людьми в зависимости от точности экспериментов, различиях в их осмыслении и иногда в силу конъюнктурных соображений. Применение той или иной физической модели в практической деятельности людей не зависит от возраста модели.
В сферу интересов физиков включены явления, связанные с устройством материи (того из чего построена вся природа) и свойства материи, определяемые этим устройством. Часто, чем ближе к физике, тем ближе к вопросу о том, как устроена материя и почему такое устройство определяет те или иные явления природы. Физические науки всегда находятся в тесном контакте с вопросами высвобождения материей энергии, то есть энергетических ресурсов человечества. Наоборот, к физическим вопросам относятся вопросы о том, - какие явления природы и как указывают на то или иное устройство материи. В силу сказанного, физика часто пересекается с другими науками, порожденными часто ранее ею, поэтому физика универсальна и может до сих пор выделять из себя другие новые науки.
11
Введение
§1 ПРЕДМЕТ И МЕТОД ФИЗИКИ
В физике изучаются формы движения материи, в чем и состоит предмет физики. Условно материя делится на поле и вещество. Вещество - все окружающие нас тела, которые мы можем наблюдать с помощью наших органов чувств.
Поля - объекты, посредством которых происходят различные взаимодействия. Поля мы можем наблюдать лишь опосредствованно через движение вещества и с помощью физических приборов. Физические приборы являются как бы дополнительными органами чувств человека.
Методом исследования в физике является опыт, эксперимент. Только эксперимент может служить прямым доказательством наличия того или иного физического закона. Теория сильна тем, что может предсказывать физические законы помимо эксперимента (хотя чаще в связи с экспериментом), но единственным доказательством справедливости закона служит только опыт, эксперимент. Точность знания законов в физике ограничена точностью экспериментов.
§2 ОСНОВНЫЕ ПОНЯТИЯ ФИЗИКИ
Событие. Всякие изменения с телами (и полями) мы будем называть событиями. События происходят в пространстве и во времени. Пространство. Пространством мы будем называть систему тел (полей), относительно которых определяется положение других тел (полей). (Абсолютное пространство - одна из моделей реального физического объекта - пространства).
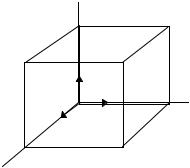
Мы живем в трехмерном Мире. Для его количественного описания Рене Декартом изобретена прямоугольная система координат: i, j, k - называются ортами осей координат x, y, z .
Z
k j |
Y |
i
X
Орты указывают направление осей координат x y z и имеют единичную длину, то есть их модули равны единице. Тогда x i, y j и z k обозначают и направление и величины координат. Координаты точки А можно символически записать как r = x i + y j + z k , где r называется радиусвектором. Итак x, y и z имеют линейные размеры. Чтобы
12

далее работать с этими величинами, необходимо определиться в системе единиц измерения - международной системе единиц, принятой в большинстве стран мира. “SI” - System International.
ЕДИНИЦЫ ИЗМЕРЕНИЯ ДЛИНЫ
(немного предыстории)
1.1675г. Длина секундного маятника.
-длина маятника, близкого к математическому и имеющего период равный единице времени в 1 секунду ( в те времена во Французской Академии наук существовала проблема воспроизводимости промежутка времени в 1 секунду). Единица длины, определенная таким способом была весьма неточной. Рассчитаем ее по формуле для периода математического маятника:
Т = 2п (l /g)1/2 l = g T2 / (2π)2 ≈ 0,25 м 1791г. Франция. Академия наук.
1 м: одна десятимиллионная часть четверти длины земного меридиана т.е. 1/40 000 000. Это было расстояние в 1100 км от Дюнкерка до Барселоны по меридиану. В дальнейшем из-за трудностей и погрешностей при повторных измерениях вместо естественного вводится архивный метр и изготавливается 31 эталон его в 1889 г. Ширина штриха в нем составляла 10 мкм, погрешность 0,1 мкм.
1960г.
1 м: 1650763,73 длин волн в вакууме перехода 2p5 - 5d10 изотопа криптона-86. Измеряется методами интерферометрии (см. раздел волновая оптика). Относительная погрешность равна 3 10 –8.
1983г. 7 – я генеральная конференция по мерам и весам (ГКМВ).
1 м: длина пути, проходимого светом в вакууме за 1/ 299792458 секунды ( скорость света постулируется при этом равной 299792458 м/с). Измеряется с помощью лазерной техники. Относительная погрешность составляет 10 -10.
ВРЕМЯ, ЕДИНИЦЫ ИЗМЕРЕНИЯ ВРЕМЕНИ
Временем будем называть показания неких часов. Часы - тело, в котором совершается периодический процесс (опять же, за часы мы выбираем те же тела: ничего другого нас нет).
|
Z |
B |
|
Y |
r2,t2 |
X |
A |
|
|
r1,t1 |
|
Произошло перемещение тела в пространстве и во времени
13
ЭТАЛОНЫ ВРЕМЕНИ
До 1960 г.
1с - 1/ 86400 часть солнечных средних суток
1960 г.
1с - 1/ 31556925,9747 часть тропического 1900 года, 1 января, полдня. Относительная погрешность - 10-7.
1972г. 8 ГКМВ.
1с = 9192631770 периодам излучения между двумя сверхтонкими уровням основного состояния Cs - 133 [m = 4, M = 0 и m = 3, M = 0, где m и M - параметры состояния атома Cs] невозмущенного внешними полями.
Таким образом, мы имеем способ, определяться в пространстве и во вре-
мени.
Однородность пространства (и времени) означает, что простая трансляция - перемещение системы замкнутых тел в пространстве (и со временем), не влияет на ход происходящих в этой системе событий и явлений.
Изотропность пространства означает, что поворот замкнутой системы тел относительно оси, произвольно проведенной в пространстве, не влияет на ход происходящих в системе событий и явлений.
14
ЧАСТЬ 1 МЕХАНИКА
Вмеханике изучаются формы движения. Движением в механике мы будем называть процессы изменения взаимного расположения тел при поступательных и вращательных формах их изменения в пространстве и со
временем.
ГЛАВА 1 КИНЕМАТИКА
К кинематика - раздел механики, в котором описывается движение тел как материальных точек. Материальной точкой называется воображаемое тело, не имеющее массы, размерами которого в условиях данной задачи можно пренебречь. Задача кинематики - описание зависимости кинематических
величин от времени: r (t), v (t), a (t), ...
§ 1 Векторы
Векторы - физические величины, имеющие направление, (а - "вектор а"). В декартовой системе координат a = ax i + ayj + azk. i, j, k- базисные векторы (орты декартовой системы координат), а x,y,z- компоненты вектора.
15
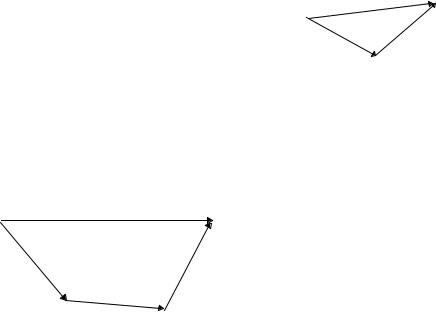
Сложение векторов геометрически (1586г, Стевин). Пусть имеем два вектора a1 и a2
Вектора складываются по правилу параллелограмма, для этого совместим начала векторов параллельным переносом и проведем в полученном параллелограмме диагональ или совместим начало и конец двух векторов и соединим начало первого с концом второго. Мы получим тот же самый результат:
a
a2 |
a1 |
a = a1 + a2
Продолжим аналогию на число векторов большее двух:
a
a1 |
a3 |
a
a = a1 + a2 + a3
Вычитание векторов определяется как действие обратное сложению, например
a2 = a - a1
Сложение векторов алгебраически, если:
a1 = a1xi + a1yj + a1zk |
и |
a2 = a2x i + a2y j + a2zk, |
то a = a1 ± a2 = (a1x ± a2x)i + (a1y ± a2y)j + (a1z ± a2z)k
- суммы или разности компонентов векторов. 16
Умножение на скаляр. α: αa - вектор в α раз больший по величине, чем величина вектора а, причем для α> 0 - того же направления, а для α< 0 - противоположного направления.
Заметим, что ax, ay и az являются сторонами прямоугольного параллелепипеда в декартовой системе координат, а поскольку a = axi + ayj + azk, где а - сумма векторов, то модуль а по определению равен а2 = аx2+ ay2+ az2 ,то есть модуль вектора а вычисляется как квадратный корень из суммы квадратов его компонентов и является диагональю прямоугольного параллелепипеда.
О скалярном произведении векторов. По определению:
а1а2 =а1а2Cos(a1^a2), при этом ii=jj=kk=11Cos 0 = 1,
ij=ik=jk=Cos (π /2)= 0.
В качестве примера возведем в квадрат сам вектор а.
( axi+ayj+azk)2 = ax2+ ay2+az2+axayij+ ... .
Вектор как тензор первого порядка
Тензор по Сокольникову И.С. Тензоры - абстрактные объекты, свойства которых не зависят от координатных систем, используемых для описания этих объектов.
Тензоры как математическое отображение физических величин - физические величины, математически так представленные, что их свойства (при таком описании) не зависят от координатных систем, используемых для представления данных физических величин. Компонентов вектора a x, ay, az недостаточно для независимого от выбора координат описания физической величины. Каждая компонента становится как бы вектором и распадается на три
новых компоненты: ax (a xx, a xy, a xz), ay (a yx, a yy, a yz), az (a zx, a zy, a zz). Тензорное преобразование предполагает независимость от выбора системы координат для
данной физической величины, и такая независимость называется инвариантностью по отношению к преобразованию координат.
17

§2 Путь, перемещение, скорость, ускорение
Рассмотрим двумерное пространство, плоскость (для простоты).
Y
 r2
r2
∆r  перемещение
перемещение
r1 траектория
X
∆г = r2 - r1 - вектор перемещения, перемещение, ∆r, - длина прямой, соединяющей начальную и конечную точки траектории
Чтобы узнать форму траектории надо знать вид зависимости y(x). Вдоль траектории отсчитывается путь.
Скорость мы будем связывать с быстротой перемещения материальной точки в пространстве. В данном случае речь идет о мгновенной скорости на пути. Рассмотрим участок траектории
Y |
r2 |
∆r
r1
X
v = lim(∆r/ ∆t) = dr/dt,
∆t→0
По определению
[v] = м/с, v = vx i + vy j + vz k, vx = dx/dt, vy = dy/dt,
vz = dy/dt, v2 = vx2 + vy2 + vz2
18

Мгновенная скорость есть первая производная от радиус-вектора по времени. Мгновенное ускорение:
a = lim ∆v/∆t = dv/dt = d2r/dt2,
∆t→0
a = axi + ayj + azk, ax = dvx/dt = d2x/dt2,
ay = dvy/dt =d2y/dt2, аz = dvz/dt = d2z/dt2, a2 = ax2 + ay2 + az2.
§ 3 Интегрирование скорости для нахождения пути
Рассмотрим задачу о том, как, зная величину скорости вычислить путь пройденный материальной точкой. Пусть нам известна зависимость модуля скорости от времени.
V |
V(t) |
vi |
t
t0 |
∆t |
tкон |
Разобьем путь S вдоль траектории на относительно небольшие участки, тогда
S = ∆s1 + ∆s2 + ... + ∆sn = ∑∆si
но так как vi = ∆si/t, то ∆si = vi ∆t, где ∆t - равные промежутки времени
S = ∑∆si = ∑ vi ∆t.
19

Суммирование производится от i = 1 до i = n - натурального числа. Это равенство приближенное и будет тем точнее, чем меньше ∆t. Точным значением будет
tкон
s= lim ∑ vi∆t = ∫ v(t) dt ∆t→0 t0
Получили определенный интеграл в пределах от t0 до tкон от вектора мгновенной скорости. Можно интегрировать вектор скорости.
tкон |
кон |
∫ v(t) dt = ∫ dr(t) = r2 - r1 = ∆r |
|
t0 |
t0 |
(v = dr/dt dr = v dt)
Средняя путевая скорость:
tкон
<v> = s/(tкон - t0) = [1/(tкон -t0)] ∫ v(t) dt, t0
средняя скорость по перемещению
tкон
<v> = ∆r/∆t = [1/(tкон - t0)] ∫ v(t) dt t0
Заметим, что среднее значение произвольной функции f(x) вычисляется по формуле
x2
<f> = [1/(x2 - x1)] ∫ f(x)dx x1
20
