
- •Глава 01 Основные понятия
- •1.1 Реальный объект и расчетная схема
- •1.3 Силы внешние и внутренние
- •1.5 Напряжения
- •1.6 Условия эквивалентности напряжений и внутренних усилий
- •1.7 Деформации
- •1.8. Потенциальная энергия упругой деформации
- •1.9 Гипотезы и допущения в сопротивлении материалов
- •1.10 Условие прочности
- •1.11. Виды опор, используемые в схемах сопротивления материалов
- •1.12. Статически определимые и статически неопределимые системы
- •1.13. Цели и задачи сопротивления материалов
- •1.14. Неучитываемые факторы
- •1.14.1 Концентрация напряжений
- •1.14.2. Изменение механических свойств материала
- •1.14.3. Вероятность выхода из строя
- •1.14.4. Принцип Сен-Венана
- •2.1 Статические моменты площади сечений
- •2.1.1. Свойства статических моментов площади сечения
- •2.1.2. Определение положения центра тяжести
- •2.2 Моменты инерции сечений
- •2.2.1. Свойства моментов инерции
- •2.2.2. Моменты инерции простейших фигур
- •2.2.4. Моменты инерции относительно повернутых осей
- •2.2.5. Главные оси и главные моменты инерции
- •2.2.6. Радиус инерции сечения
- •Глава 03 Определение внутренних усилий
- •3.1 Растяжение-сжатие
- •3.2 Кручение
- •3.3 Изгиб
- •3.4.1. Растяжение-сжатие
- •3.4.2. Кручение
- •3.4.3. Изгиб
- •3.4.4. Следствия из дифференциальных зависимостей
- •Глава 04 Растяжение-сжатие
- •4.1 Внутренние усилия и напряжения
- •4.2 Деформации
- •4.3 Закон Гука
- •4.4 Потенциальная энергия упругой деформации
- •4.5 Напряжения на наклонных площадках
- •4.6. Закон парности касательных напряжений
- •4.7 Понятие о главных напряжениях
- •5.2 Диаграмма деформирования мягкой стали
- •5.2.1. Характеристики прочности
- •5.2.2. Характеристики пластичности
- •5.2.3. Работа разрушения при разрыве
- •5.2.4. Диаграммы деформирования других материалов
- •5.3 Испытание материалов на сжатие
- •5.4 Допускаемые напряжения
- •Глава 06 Сдвиг и кручение
- •6.1 Сдвиг
- •6.2 Расчет простейших соединений
- •6.2.1. Расчет тяги
- •6.2.2. Расчет штифта (заклепки)
- •6.2.3. Расчет сварного соединения
- •6.3 Кручение стержней круглого поперечного сечения
- •6.3.1. Касательные напряжения и угол закручивания
- •6.3.2 Потенциальная энергия при кручении стержня
- •6.4. Связь между крутящим моментом, мощностью и скоростью вращения вала
- •6.5. Кручение стержней некруглого поперечного сечения
- •Глава 07 Плоский поперечный изгиб
- •7.1 Нормальные напряжения при изгибе балки
- •7.1.1. Условие прочности при изгибе
- •7.1.2. Рациональная форма поперечного сечения
- •7.2 Касательные напряжения при изгибе
- •7.2.2. Проверка прочности по касательным напряжениям
- •7.4 Перемещения при изгибе
- •7.4.1. Непосредственное интегрирование уравнения упругой линии балки
- •7.4.2. Метод начальных параметров
- •7.5 Изгиб кривых брусьев
- •7.6 Расчет балок на упругом основании
- •8.1 Связь напряжений и деформаций
- •8.3 Учет пластических деформаций при изгибе
- •8.4 Учет пластических деформаций при кручении
- •8.5 Расчеты по предельной нагрузке
- •8.6. Понятие о приспособляемости конструкций
- •9.1. Деформации
- •9.2. Напряжения
- •9.3. Виды напряженного состояния
- •9.4. Плоское напряженное состояние
- •9.4.1. Прямая задача
- •9.4.2. Обратная задача
- •9.6 Гипотезы прочности и пластичности
- •9.7. Условие прочности при плоском напряженном состоянии
- •Глава 10 Сложное сопротивление
- •10.1.Внутренние усилия при сложном сопротивлении
- •10.1.1. Построение эпюр внутренних усилий
- •10.2 Напряжения
- •10.3.1. Стержень произвольного сечения
- •10.3.2. Прямоугольное сечение
- •10.3.3. Круглое или кольцевое сечение
- •10.4. Частные случаи сложного сопротивления
- •11.1 Интеграл Мора
- •11.1.1. Определение перемещений в кривом брусе
- •11.1.2. Порядок определения перемещений с помощью интеграла Мора
- •11.2 Метод сил
- •11.2.1. Степень статической неопределимости
- •11.2.2. Перемещение от единичной силы (коэффициент податливости)
- •11.2.3. Канонические уравнения метода сил
- •11.2.4. Учет монтажных и температурных напряжений
- •11.2.5. Учет симметрии в методе сил
- •11.2.6. Проверка правильности решения системы
- •11.2.7. Порядок решения статически неопределимой задачи методом сил
- •11.3. Определение перемещений систем из нескольких элементов
- •Глава 12 Устойчивость сжатых стержней
- •12.1. Определение критической силы. Формула Эйлера
- •12.2. Определение критической силы при других видах закрепления
- •12.3. Критические напряжения
- •12.4. Расчет сжатых стержней на устойчивость
- •12.4.1. Примечания к расчету на устойчивость
- •12.5 Энергетический метод определения критической силы
- •12.6 Продольно-поперечный изгиб
- •Глава 13 Расчет тонкостенных оболочек
- •13.1 Безмоментная теория тонкостенных оболочек
- •13.1.1. Гипотезы и допущения
- •13.1.2. Формула Лапласа
- •13.1.3.Частные случаи тонкостенных оболочек
- •13.1.4. Расчет на прочность
- •13.2 Расчет распорного кольца
- •13.3 Деформация трубы под давлением
- •13.4 Краевой эффект
- •Глава 14 Динамика упругих систем
- •14.1. Учет сил инерции при движении тела
- •14.2. Колебания упругой системы
- •14.2.1. Уравнение движения системы с одной степенью свободы
- •14.2.2. Свободные затухающие колебания.
- •14.2.3. Опытное определение коэффициента затухания колебаний
- •14.3. Определение собственной частоты системы с одной степенью свободы
- •14.3.1. Без учета собственной массы системы
- •14.3.2. С учетом собственной массы системы
- •14.3.3. Крутильные колебания
- •14.3.4. Замечания к расчету собственных частот колебаний
- •14.4.Ударная нагрузка
- •14.4.1.Вертикальный удар
- •14.4.2. Горизонтальный удар
- •14.4.3. Крутящий удар
- •14.4.4. Замечания к расчетам на ударную нагрузку
- •14.5. Вынужденные колебания системы с одной степенью свободы
- •14.5.1. Импульс силы
- •14.5.2. Произвольная нагрузка
- •14.5.3. Гармоническое действие силы
- •14.5.4. Критическая скорость вращения вала
- •Глава 15 Усталость материалов
- •15.1. Механизм усталостного разрешения
- •15.2. Характеристики цикла нагружения
- •15.3. Диаграммы усталостной прочности
- •15.3.1. Усталостная кривая
- •15.3.2. Диаграмма предельных амплитуд
- •15.3.3. Приближенное построение диаграмм усталостной прочности
- •15.4. Суммирование повреждений при нестационарной нагрузке
- •15.5.1. Концентрация напряжений
- •15.5.2. Размеры детали
- •15.5.3. Состояние поверхности
- •15.5.4. Поверхностное упрочнение
- •15.5.5. Влияние коррозии
- •15.5.6. Влияние температуры
- •15.6. Предел выносливости детали
- •15.7. Расчет на усталостную прочность
- •15.8. Понятие о малоцикловой усталости
- •Глава 16 Природа разрушения твердых тел
- •16.1. Природа упругой деформации
- •16.2. Теоретическая прочность твердых тел
- •16.4. Виды дислокаций
- •16.5. Размножение дислокаций
- •16.6. Механизмы упрочнения
- •16.7. Механизм больших пластических деформаций
- •16.8. Механизмы образования трещин
- •16.9. Механизмы роста трещин
- •16.10. Механизмы пластического разрушения
- •16.11.Механизм хрупкого разрушения
- •Глава 17 Факторы, влияющие на прочность и разрушение материалов
- •17.1. Скорость деформации
- •17.2. Температура эксплуатации
- •17.4. Напряженное состояние
- •17.5. Остаточные напряжения
- •Глава 18 Механика разрушения тел с трещинами
- •18.1. Основные гипотезы
- •18.2. Критерии трещиностойкости
- •18.3. Живучесть конструкций
- •19.1. Выбор рациональной конструкции
- •19.2. Выбор критериев оптимизации
- •Список литературы
Примечание
Любой цикл нагружения можно представить как сумму симметричного цикла (σa ) и постоянной нагрузки (σm )
15.3. Диаграммы усталостной прочности
Для расчетов деталей на прочность и долговечность рассмотрим две основные диаграммы усталостной прочности.
15.3.1. Усталостная кривая
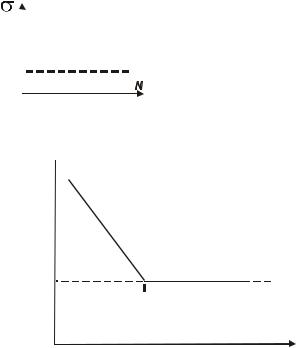
Эта диаграмма показывает зависимость числа циклов до разрушения N от максимальных напряжений в детали σ . Впервые такая диаграмма была построена немецким инженером Велером и по его имени названа диаграмма Велера. Диаграмма строится по результатам лабораторных испытаний серии образцов.
Для построения одной кривой испытывается не менее 10 образцов. Каждая точка на диаграмме соответствует испытанию до разрушения одного образца.
Образец испытывается при циклической нагрузке с постоянной величиной максимального напряжения цикла σ , записывается число циклов до разрушения N . Точка с координатами σ, N наносится на график.
На графике по экспериментальным точкам проводится усредняющая их кривая (рис. 15.6). При некотором значении σ долговечность (число циклов до разрушения)
N стремится в бесконечность.
Пределом выносливости (усталости) называется максимальное напряжение, при котором образец не разрушается при числе циклов, равном бесконечности.
Обозначение предела выносливости σr , где r — характеристика цикла нагружения, например: σ−1 — при симметричном цикле, σ0 — при пульсирующем цикле.
На диаграмме Велера трудно одноврменно показать точки с малым и большим числом циклов до разрушения. Так точки с долговечностью N < 1000 циклов практически сливаются с осью σ .
Чтобы раздвинуть точки на графике, на практике усталостную кривую строят в логарифмических координатах lgσ − lg N , в которых кривая апроксимируется
двумя отрезками прямой линии. Наклонной прямой, соответствующей, так называемой, ограниченной выносливости образцов, когда испытание заканчивается разрушением образца, и горизонтальной прямой, соответствующей пределу выносливости (рис. 15.7).
Усталостная кривая, на самом деле, является кривой линией, но ввиду огромного разброса опытных данных, ее можно аппроксимировать отрезками прямых линий.
σr 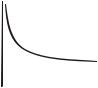
Рис. 15.6 Кривая Велера
lg σ 
lgσr
|
|
lg N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lg N 0 |
||
Рис. 15.7 Усталостная кривая в логарифмических координатах
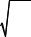
Долговечность, соответствующая пересечению прямых называется базовым числом циклов N0 . При приближенном построении усталостной кривой принимают
N0 ≈ (1−3) 106 циклов для всех черных металлов (чугуна и сталей).
Для цветных металлов, а также при испытании черных металлов в коррозионных средах, предел выносливости не существует и вторая прямая не горизонтальная, а наклонная (ее угол наклона в несколько раз меньше, чем для первой прямой.
Для определения предела выносливости и построения усталостной кривой необходимо испытать серию из 10 – 20 образцов. Чаще всего образец нагружается изгибом при вращении образца или плоским изгибом (оборудование для таких испытаний наиболее простое). Нагрузка на образец — постоянная.
Для первого образца устанавливается нагрузка, создающая в образце напряжения maxσ = 0,5(σв +σт) . Образец испытывается до разрушения и записывается число циклов до разрушения образца.
Для второго образца нагрузка снижается, Образец также испытывается до разрушения. Число циклов до разрушения при этом увеличивается.
Результаты испытаний наносятся на график в логарифмических координатах. Несмотря на существенный разброс опытных точек их апроксимируют усредняющей прямой линией. Часто используется статистическая обработка результатов испытаний методом наименьших квадратов.
Если образец не сломался после 10 млн циклов, испытание прекращается. Считается, что достигнут предел выносливости, но для статистической обработки на этом же уровне нагрузки или близких к нему испытывается еще несколько образцов.
Для испытаний используются стандартные полированные образцы диаметром d0 = 5 − 7,5 мм. Требования к изготовлению образцов и методика испытаний на выносливость (усталость) изложены в ГОСТ 25.504–82.
Для расчетов на ограниченную выносливость, то есть для деталей, испытывающих за весь срок службы меньше 2 млн циклов, записывают уравнение для наклонного участка усталостной кривой. В логарифмических координатах
lg N = lg A − m lgσ , |
где |
A |
и |
m |
—эмпирические |
коэффициенты. Отсюда |
||||||
Nσ m = Const = N σ m |
— уравнение усталостной прочности. |
|||||||||||
|
|
|
|
0 |
r |
|
|
|
|
|
|
|
Зная предел выносливости σr |
и базовое число циклов |
N0 = 3 106 можно найти |
||||||||||
долговечность при заданном напряжении |
|
|
||||||||||
|
|
σ |
|
m |
|
|
|
|
|
|
(15.1) |
|
N = N0 |
|
r |
|
|
|
|
|
|
||||
|
|
σ |
|
|
|
|
|
|
|
|||
или напряжение, соответствующее заданной долговечности |
||||||||||||
σ =σr m |
|
N0 |
|
|
|
|
|
|
(15.2). |
|||
|
|
N |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициент m |
часто |
берется |
из |
справочников. Обычно m = 8 −12 . При |
||||||||
отсутствии экспериментальных данных предел выносливости при симметричном цикле часто оценивают по приближенным формулам:
σ−1изгиба ≈ (0, 4 − 0,5)σв
σ−1растяжения ≈ (0,7 − 0,8)σ−1изгиба |
(15.3) |
τ−1кручения ≈ 0,5σ−1изгиба . |
|
Поскольку усталостное разрушение сопровождается огромным разбросом по долговечности, при обработке результатов испытаний желательна статистическая обработка результатов (обычно методом наименьших квадратов).
На рис.15.8 показана зона рассеивания результатов испытаний на усталость. Ее верхняя граница соответствует вероятности неразрушения p = 0,1%, нижняя —
p = 99,9 %. Обработка результатов испытаний серии образцов с построением доверительного интервала долговечности приведена в электронной книге.
Следует отметить, что разброс данных по долговечности во много раз больше, чем по напряжениям. Так снижение напряжений на 20% ведет к увеличению средней долговечности примерно в 10 раз.
p= 0,1%
lg σ
p= 99,9%
0,8σ 




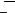



N
lg N
Рис. 15.8 Рассеивание результатов испытаний на усталость
Если статистическая обработка не производится, вероятность неразрушения можно увеличить с помощью коэффициента запаса. При использовании в расчетах средневероятностной усталостной кривой коэффициент запаса по напряжениям n = 1 соответствует вероятности неразрушения 50%, n = 1, 5 — 99%, n = 2 – 99,9%.
15.3.2. Диаграмма предельных амплитуд
Для определения предела выносливости при асимметричном цикле необходимо проведение испытаний при соответствующей характеристике цикла r .
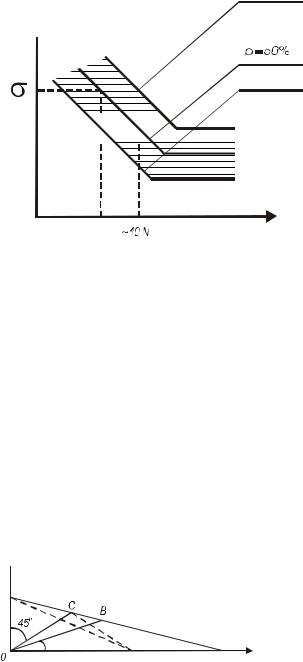
Определив пределы выносливости при нескольких значениях коэффициента r , можно построить диаграмму для определения предела выносливости при любом асимметричном цикле, называемую диаграммой предельных амплитуд. Получить опытные данные для такой диаграммы чрезвычайно сложное и трудоемкое дело и на практике используют приближенную диаграмму, построенную по 2-м или 3-м точкам
(рис. 15.9).
σа 
σ−1
β |
|
Sк σ |
m |
|
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|
||
|
|
σв |
|
|
Рис. 15.9 Диаграмма предельных амплитуд |
|
|
||
Диаграмма строится в координатах σa −σm . |
Отрезки, |
отсекаемые диаграммой на |
||
осях координат: σ−1 — на оси σa (при σm = 0 ) и σв |
— на оси σm (при σa = 0 ). |
|||
Для определения предела выносливости при заданном значении r |
надо из начала |
|||||||
координат провести луч под углом β , для которого |
|
|||||||
tgβ = |
σa |
= |
(σmax −σmin ) |
= |
1 |
− r |
|
(15.4). |
|
(σmax +σmin ) |
|
+ r |
|||||
σm |
|
1 |
|
|||||
Сумма координат точки В пересечения луча ОВ c диаграммой предельных амплитуд
представляет |
собой предел выносливости при заданном коэффициенте r |
||
σ |
r |
=σ B +σ B . |
|
|
m |
a |
|
Для построения диаграммы по 2-м точкам чаще всего используют предел прочности σв и предел выносливости при симметричном цикле σ−1 . На осях координат
откладывают σв и σ−1 и соединяют две точки прямой линией. В этом случае уравнение диаграммы предельных амплитуд
σa =σ−1 −ψ σm |
(15.5), |
|
где ψ = |
σ−1 — угловой коэффициент. |
|
|
σв |
|
В наших расчетах вместо предела прочности при построении диаграммы предельных амплитуд используется сопротивление разрыву Sк . Ведь предел прочности σв
характеризует сопротивление пластической деформации, а Sк — сопротивление
разрушению. Эксперименты показали, что использование сопротивления разрыву при построении усталостной кривой и диаграммы предельных амплитуд позволяет значительно повысить точность оценки усталостной прочности. В этом случае
ψ = σ−1 .
Sк
В расчетах деталей машин на усталостную прочность часто используют апроксимацию Серенсена С.В., в которой в качестве третьей точки при построении диаграммы предельных амплитуд используется предел выносливости при пульсирующем цикле σ0 ( r = 0 , точка С на рис. 15.9). Тогда апроксимация
диаграммы представляет собой два отрезка прямых линий. Расчетное уравнение
диаграммы имеет тот же вид, что и в случае 2-х точек, но ψ = |
2σ−1 −σ0 |
≈ 0,1− 0,3 . |
||||
σ0 |
||||||
Чаще всего величина ψ |
|
|
|
|
||
берется из справочников. Апроксимация Серенсена С.В. |
||||||
дает почти те же результаты, что и использование |
Sк при построении диаграммы |
|||||
предельных амплитуд. |
|
|
|
|
|
|
Совет |
|
|
разрыву Sк можно |
|
||
При отсутствии в |
справочнике |
сопротивления |
приближенно |
|||
принять Sк ≈ 2 σв |
или Sк σв |
≈ 1 + 1, 4 ψk . |
|
|
|
|
15.3.3. Приближенное построение диаграмм усталостной прочности
Для приближенной оценки долговечности конструкций и деталей машин необходимо уметь приближенно строить диаграммы усталостной прочности, без проведения длительных испытаний на усталость, только с использованием данных, приведенных в справочниках. Там, как правило, нет других механических характеристик, кроме предела текучести и предела прочности.
Рассмотрим пример построения таких диаграмм. Для большей наглядности построения расчет произведен в числах.
Для стали 40Х улучшенной (термообработка — закалка с высоким отпуском) σв =1000 Мпа определить предел ограниченной выносливости для долговечности
N =105 циклов при изгибе симметричным циклом нагружения r = −1 и асимметричным циклом r = 0,5 .
lg σ
lgSk
lgσ0,5,105
lgσ0,5
lgσ−1,105
lgσ−1 













lg N 0 |
lg N |
|
Рис. 15.10. Усталостная кривая при симметричном и асимметричном циклах нагружения
Построим усталостную кривую в логарифмических координатах приближенно по 2-м точкам, соответствующим статическому разрыву и пределу выносливости при симметричном цикле (рис. 15.10).
Статическому разрыву соответствуют 1 4 или 1/2 цикла нагружения. Поскольку расчет очень приближенный, принимаем для статического разрыва N =1. Пределу выносливости на усталостной кривой соответствует точка с координатами σ−1 и
4 или 1/2 цикла нагружения. Поскольку расчет очень приближенный, принимаем для статического разрыва N =1. Пределу выносливости на усталостной кривой соответствует точка с координатами σ−1 и
N0 = 3 106 циклов для сталей.
