Рис. 14.9. Формы колебания консольной балки

Наибольшие деформации и напряжения в любой системе возникают при резонансе на первой собственной частоте, поэтому для расчета на прочность важно знать именно первую (низшую) собственную частоту.

Формулы (14.8) и (14.13) можно использовать и при расчете рам для определения первой собственной частоты. При этом ошибка может быть довольно большой.

Не следует забывать, что расчеты на прочность вообще не отличаются высокой точностью. Какими бы точными не были расчетные формулы, ошибка в определении механических свойств материала и в выборе коэффициента запаса, необходимость учета вероятности разрушения не позволяют достигнуть высокой точности расчета.

Ориентировочно можно определить и первую собственную частоту сложной конструкции. Допустим: перед вами "черный ящик" — сложная конструкция с исполнительным органом-рычагом. Для оценки его собственной частоты определим

жесткость конструкции. Подвесим на рычаг любой груз весом F и измерим

перемещение стат под действием этого груза. Тогда жесткость k = F . По

стат

формуле (14.8) определяем ориентировочную низшую собственную частоту конструкции.

Рабочая частота исполнительного органа не должна приближаться к собственной частоте колебаний конструкции. Если простейший расчет по формуле (14.8) показывает близость таких частот, надо изменить жесткость системы или ее массу.

Порой достаточно положить на раму мешок с песком, чтобы резко уменьшить собственную частоту конструкции, или приварить какую-нибудь перекладину, чтобы увеличить жесткость и собственную частоту.

14.4.Ударная нагрузка

Действие на систему с одной степенью свободы ударной нагрузки рассмотрим как частный случай колебаний.

Далее излагается приближенная теория удара, основанная на ряде упрощающих расчет допущений.

Ударяющее тело абсолютно жесткое.

Удар происходит без отскока, то есть практически ударяющее тело прилипает к ударяемому.

Справедлив закон Гука. Пластических деформаций нет Не учитывается волновой характер удара.

Есть некоторые особенности в рассмотрении вертикального, горизонтального и крутящего удара.

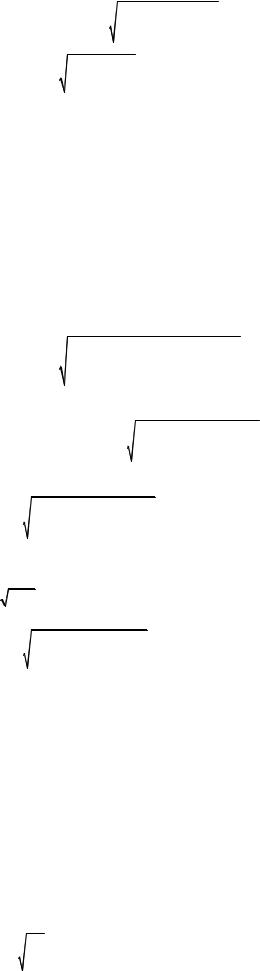
14.4.1.Вертикальный удар

После удара начинается совместное колебательное движение системы груз-балка. Перемещение точки соударения u во времени показано справа на рис. 14.9.

m

Колебания — затухающие. После остановки колебаний точка соударения займет

При затухающих колебаниях максимальная амплитуда колебаний достигается в первом полупериоде. Соответственно в этот момент динамические напряжения в

балке будут наибольшие. Дальнейшие колебания можно не учитывать. Такой процесс называют квазистатическим.

Затуханием колебаний в этом процессе можно пренебречь. Коэффициент затухания колебаний в дальнейших расчетах полагаем равным нулю h = 0 .

Динамическое перемещение точки соударения представим как сумму статического

В этом выражении V0 — скорость движения системы груз-балка в начальный

момент колебаний. Для ее нахождения воспользуемся теоремой о количестве движения.

mV = (m + kпрm0 )V0 .

Здесь mV — количество движения падающего груза перед ударом,

(m + kпрm0 )V0 — количество движения системы груз-балка в момент начала колебаний. Тогда

Поскольку деформации при ударе считаем упругими, то напряжения пропорциональны перемещениям и возрастают при ударе во столько же раз, что и перемещения

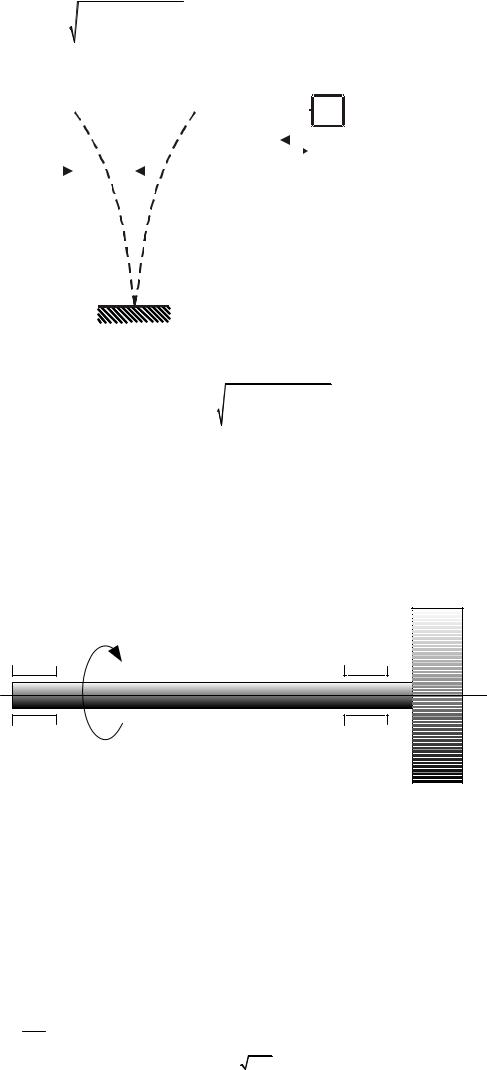
14.4.2. Горизонтальный удар

Рассмотрим вертикальную балку, в которую ударяется груз массой m , движущийся горизонтально (рис. 14.11).

После совместного колебания система груз-балка останавливается в положении стат = 0 . Поэтому динамическое перемещение точки соударения равно

максимальной амплитуде колебаний дин = A . Тогда выражение (14.14) примет вид

Подставим выражения V0 (14.15) и ω (14.13) в выражение дин получаем

m

u=00

Рис. 14.11. Перемещения при горизонтальном ударе

Окончательно для расчета при горизонтальном ударе получаем

14.4.3. Крутящий удар

При крутящем ударе нет понятия коэффициент динамичности, так как энергию вращающегося тела нельзя связать с какой-либо статической нагрузкой. В такой задаче надо использовать закон сохранения энергии T = П. Кинетическая энергия ударяющего тела T равна потенциальной энергии упругой деформации П системы тел (ударяющего и ударяемого).

Общей формулы для решения задач на крутящий удар нет.

Кинетическая энергия вращающегося вала

T = ( Jm + kпр Jm0 )ω2 ,

2

k = GJLp — жесткость вала при кручении.

Тогда из условия T = П находим Mк.д = 2kT .