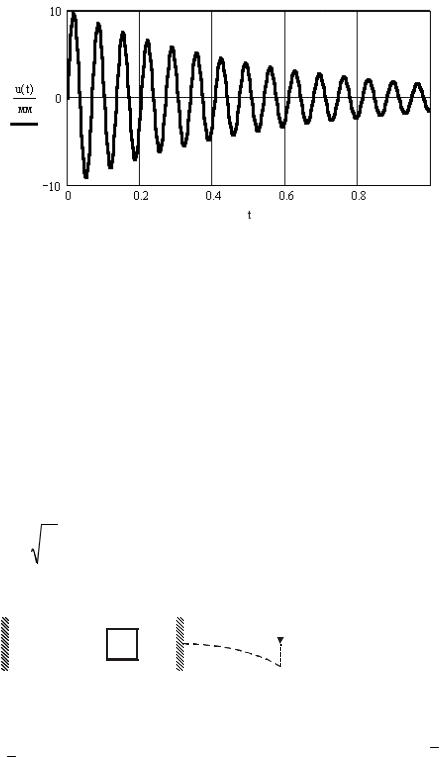
14.2.3. Опытное определение коэффициента затухания колебаний

Затухание колебаний оценивается логарифмическим декрементом

где ui и ui+1 — амплитуда двух соседних пиков колебаний (рис. 14.5).

Запишем отношение амплитуд колебаний с использованием выражения (14.4)

Рис. 14.6. Экспериментальная диаграмма затухающих колебаний

Для определения коэффициента затухания надо иметь график затухающих колебаний. Например, стукнуть кулаком по балке и записать изменение амплитуды колебаний на диаграмму или осциллограмму (рис. 14.6). Определить логарифмический декремент по формуле (14.6) и коэффициент затухания по формуле

(14.7).

14.3. Определение собственной частоты системы с одной степенью свободы

Рассмотрим два варианта определения собственной частоты: без учета собственной массы системы и с учетом этой массы.

14.3.1. Без учета собственной массы системы

Для системы с одной степенью свободы собственная частота ω определятся по уравнению (14.2) как

податливости δ , а податливость — это статическое перемещение от единичной силы

F =1, определяемое чаще всего с помощью интеграла Мора δ11 = ∑∫M 2dS .

L EJ

Для определения жесткости системы изобразим систему, нагруженную сосредоточенной силой (любой), приложенной в точке, где находится сосредоточенная масса, в направлении перемещения точки в процессе колебаний (в направлении степени свободы).

Если при определении жесткости в качестве силы взять вес груза, формулу (14.8)

можно упростить. Пусть F = mg = k стат , тогда k = mg , где стат — перемещение

стат

от веса груза. Подставив k в формулу (14.8), получаем собственную (круговую) частоту системы

Зная круговую частоту ω , можно определить частоту колебаний f (герц) и период колебаний T

14.3.2. С учетом собственной массы системы

Рассмотрим консольную балку массой m0 с сосредоточенной массой m на конце балки (рис. 14.8). Если массу балки m0 считать распределенной, система имеет бесконечное число степеней свободы.

Чтобы рассматривать ее как систему с одной степенью свободы, надо распределенную массу заменить сосредоточенной, приложенной в той же точке, что и масса m . Собственную частоту определим для системы с сосредоточенной массой

m + kпрm0 , где kпр — коэффициент приведения массы.

m0

Рис. 14.8. К расчету собственной частоты с учетом массы системы

Условием приведения массы является равенство кинетических энергий систем с распределенной Tраспред и с сосредоточенной приведенной Tсосред массой.

Распределение скоростей по длине балки неизвестно. Примем гипотезу:

распределение скоростей пропорционально распределению перемещений по длине балки.

Эта гипотеза справедлива для достаточно жестких тел при сравнительно малых собственных частотах (порядка первой собственной частоты). Тогда

После приведения всех масс в одну точку получили систему с одной степенью свободы. Ее собственная частота

14.3.3. Крутильные колебания

При крутильных колебаниях роль массы m исполняет момент инерции массы Jm . Уравнение колебательного движения имеет вид

Jm d 2ϕ2 + 2hJm dϕ + kϕ = M (t) . dt dt

Здесь k — жесткость стержня при кручении. Жесткости при кручении и при изгибе — разные.

Решение этого уравнения аналогично решению уравнения (14.1). Соответственно подобным получается и выражение для круговой частоты ω

14.3.4. Замечания к расчету собственных частот колебаний

В этом разделе рассматривается только определение собственной частоты системы с одной степенью свободы, как правило, для прямых стержней. Для рам и кривых брусьев движение точек в процессе колебаний происходит по сложным криволинейным траекториям и следует учитывать несколько степеней свободы. В этом случае расчет многократно усложняется.

Расчет колебаний систем с большим числом степеней свободы лучше всего производить с использованием метода конечных элементов. Примеры динамических расчетов методом конечных элементов можно посмотреть в моей книге "Инженерные расчеты в Mathcad" [18, 19] и использовать в своих расчетах.

Для различных случаев колебания двух-трех массовых систем готовые формулы для определения собственных частот можно найти в справочниках.

Следует иметь в виду, что от того, что мы решили рассмотреть балку, как систему с одной степенью свободы, она не перестала быть системой с бесконечным числом степеней и с бесконечным количеством собственных частот.

На рис. 14.9 приведены формы колебания на первых трех собственных частотах консольной балки. Собственные частоты ωι и максимальные амплитуды колебаний

Ai приведены для линейки из оргстекла длиной 0,5 м. Заметим, что никакой

кратности собственных частот не наблюдается. Амплитуда колебаний максимальна для первой (низшей) собственной частоты. Для второй уже в три раза меньше, для третьей в 10 раз меньше, чем для первой. Для четвертой собственной частоты амплитуда исчезающе мала. Если дотронутся рукой можно ощутить дрожание линейки, но померить уже нельзя.