
- •Глава 01 Основные понятия
- •1.1 Реальный объект и расчетная схема
- •1.3 Силы внешние и внутренние
- •1.5 Напряжения
- •1.6 Условия эквивалентности напряжений и внутренних усилий
- •1.7 Деформации
- •1.8. Потенциальная энергия упругой деформации
- •1.9 Гипотезы и допущения в сопротивлении материалов
- •1.10 Условие прочности
- •1.11. Виды опор, используемые в схемах сопротивления материалов
- •1.12. Статически определимые и статически неопределимые системы
- •1.13. Цели и задачи сопротивления материалов
- •1.14. Неучитываемые факторы
- •1.14.1 Концентрация напряжений
- •1.14.2. Изменение механических свойств материала
- •1.14.3. Вероятность выхода из строя
- •1.14.4. Принцип Сен-Венана
- •2.1 Статические моменты площади сечений
- •2.1.1. Свойства статических моментов площади сечения
- •2.1.2. Определение положения центра тяжести
- •2.2 Моменты инерции сечений
- •2.2.1. Свойства моментов инерции
- •2.2.2. Моменты инерции простейших фигур
- •2.2.4. Моменты инерции относительно повернутых осей
- •2.2.5. Главные оси и главные моменты инерции
- •2.2.6. Радиус инерции сечения
- •Глава 03 Определение внутренних усилий
- •3.1 Растяжение-сжатие
- •3.2 Кручение
- •3.3 Изгиб
- •3.4.1. Растяжение-сжатие
- •3.4.2. Кручение
- •3.4.3. Изгиб
- •3.4.4. Следствия из дифференциальных зависимостей
- •Глава 04 Растяжение-сжатие
- •4.1 Внутренние усилия и напряжения
- •4.2 Деформации
- •4.3 Закон Гука
- •4.4 Потенциальная энергия упругой деформации
- •4.5 Напряжения на наклонных площадках
- •4.6. Закон парности касательных напряжений
- •4.7 Понятие о главных напряжениях
- •5.2 Диаграмма деформирования мягкой стали
- •5.2.1. Характеристики прочности
- •5.2.2. Характеристики пластичности
- •5.2.3. Работа разрушения при разрыве
- •5.2.4. Диаграммы деформирования других материалов
- •5.3 Испытание материалов на сжатие
- •5.4 Допускаемые напряжения
- •Глава 06 Сдвиг и кручение
- •6.1 Сдвиг
- •6.2 Расчет простейших соединений
- •6.2.1. Расчет тяги
- •6.2.2. Расчет штифта (заклепки)
- •6.2.3. Расчет сварного соединения
- •6.3 Кручение стержней круглого поперечного сечения
- •6.3.1. Касательные напряжения и угол закручивания
- •6.3.2 Потенциальная энергия при кручении стержня
- •6.4. Связь между крутящим моментом, мощностью и скоростью вращения вала
- •6.5. Кручение стержней некруглого поперечного сечения
- •Глава 07 Плоский поперечный изгиб
- •7.1 Нормальные напряжения при изгибе балки
- •7.1.1. Условие прочности при изгибе
- •7.1.2. Рациональная форма поперечного сечения
- •7.2 Касательные напряжения при изгибе
- •7.2.2. Проверка прочности по касательным напряжениям
- •7.4 Перемещения при изгибе
- •7.4.1. Непосредственное интегрирование уравнения упругой линии балки
- •7.4.2. Метод начальных параметров
- •7.5 Изгиб кривых брусьев
- •7.6 Расчет балок на упругом основании
- •8.1 Связь напряжений и деформаций
- •8.3 Учет пластических деформаций при изгибе
- •8.4 Учет пластических деформаций при кручении
- •8.5 Расчеты по предельной нагрузке
- •8.6. Понятие о приспособляемости конструкций
- •9.1. Деформации
- •9.2. Напряжения
- •9.3. Виды напряженного состояния
- •9.4. Плоское напряженное состояние
- •9.4.1. Прямая задача
- •9.4.2. Обратная задача
- •9.6 Гипотезы прочности и пластичности
- •9.7. Условие прочности при плоском напряженном состоянии
- •Глава 10 Сложное сопротивление
- •10.1.Внутренние усилия при сложном сопротивлении
- •10.1.1. Построение эпюр внутренних усилий
- •10.2 Напряжения
- •10.3.1. Стержень произвольного сечения
- •10.3.2. Прямоугольное сечение
- •10.3.3. Круглое или кольцевое сечение
- •10.4. Частные случаи сложного сопротивления
- •11.1 Интеграл Мора
- •11.1.1. Определение перемещений в кривом брусе
- •11.1.2. Порядок определения перемещений с помощью интеграла Мора
- •11.2 Метод сил
- •11.2.1. Степень статической неопределимости
- •11.2.2. Перемещение от единичной силы (коэффициент податливости)
- •11.2.3. Канонические уравнения метода сил
- •11.2.4. Учет монтажных и температурных напряжений
- •11.2.5. Учет симметрии в методе сил
- •11.2.6. Проверка правильности решения системы
- •11.2.7. Порядок решения статически неопределимой задачи методом сил
- •11.3. Определение перемещений систем из нескольких элементов
- •Глава 12 Устойчивость сжатых стержней
- •12.1. Определение критической силы. Формула Эйлера
- •12.2. Определение критической силы при других видах закрепления
- •12.3. Критические напряжения
- •12.4. Расчет сжатых стержней на устойчивость
- •12.4.1. Примечания к расчету на устойчивость
- •12.5 Энергетический метод определения критической силы
- •12.6 Продольно-поперечный изгиб
- •Глава 13 Расчет тонкостенных оболочек
- •13.1 Безмоментная теория тонкостенных оболочек
- •13.1.1. Гипотезы и допущения
- •13.1.2. Формула Лапласа
- •13.1.3.Частные случаи тонкостенных оболочек
- •13.1.4. Расчет на прочность
- •13.2 Расчет распорного кольца
- •13.3 Деформация трубы под давлением
- •13.4 Краевой эффект
- •Глава 14 Динамика упругих систем
- •14.1. Учет сил инерции при движении тела
- •14.2. Колебания упругой системы
- •14.2.1. Уравнение движения системы с одной степенью свободы
- •14.2.2. Свободные затухающие колебания.
- •14.2.3. Опытное определение коэффициента затухания колебаний
- •14.3. Определение собственной частоты системы с одной степенью свободы
- •14.3.1. Без учета собственной массы системы
- •14.3.2. С учетом собственной массы системы
- •14.3.3. Крутильные колебания
- •14.3.4. Замечания к расчету собственных частот колебаний
- •14.4.Ударная нагрузка
- •14.4.1.Вертикальный удар
- •14.4.2. Горизонтальный удар
- •14.4.3. Крутящий удар
- •14.4.4. Замечания к расчетам на ударную нагрузку
- •14.5. Вынужденные колебания системы с одной степенью свободы
- •14.5.1. Импульс силы
- •14.5.2. Произвольная нагрузка
- •14.5.3. Гармоническое действие силы
- •14.5.4. Критическая скорость вращения вала
- •Глава 15 Усталость материалов
- •15.1. Механизм усталостного разрешения
- •15.2. Характеристики цикла нагружения
- •15.3. Диаграммы усталостной прочности
- •15.3.1. Усталостная кривая
- •15.3.2. Диаграмма предельных амплитуд
- •15.3.3. Приближенное построение диаграмм усталостной прочности
- •15.4. Суммирование повреждений при нестационарной нагрузке
- •15.5.1. Концентрация напряжений
- •15.5.2. Размеры детали
- •15.5.3. Состояние поверхности
- •15.5.4. Поверхностное упрочнение
- •15.5.5. Влияние коррозии
- •15.5.6. Влияние температуры
- •15.6. Предел выносливости детали
- •15.7. Расчет на усталостную прочность
- •15.8. Понятие о малоцикловой усталости
- •Глава 16 Природа разрушения твердых тел
- •16.1. Природа упругой деформации
- •16.2. Теоретическая прочность твердых тел
- •16.4. Виды дислокаций
- •16.5. Размножение дислокаций
- •16.6. Механизмы упрочнения
- •16.7. Механизм больших пластических деформаций
- •16.8. Механизмы образования трещин
- •16.9. Механизмы роста трещин
- •16.10. Механизмы пластического разрушения
- •16.11.Механизм хрупкого разрушения
- •Глава 17 Факторы, влияющие на прочность и разрушение материалов
- •17.1. Скорость деформации
- •17.2. Температура эксплуатации
- •17.4. Напряженное состояние
- •17.5. Остаточные напряжения
- •Глава 18 Механика разрушения тел с трещинами
- •18.1. Основные гипотезы
- •18.2. Критерии трещиностойкости
- •18.3. Живучесть конструкций
- •19.1. Выбор рациональной конструкции
- •19.2. Выбор критериев оптимизации
- •Список литературы
Пример определения величины и направления главных напряжений в Mathcad приведен в электронной книге.
9.3. Виды напряженного состояния
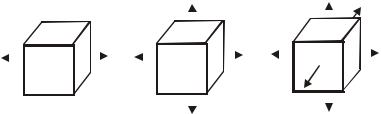
В зависимости от количества неравных нулю главных напряжений различают объемное, плоское и линейное напряженные состояния (рис. 9.3).
|
|
a) |
|
|
|
б) σ |
|
|
|
в) |
|
σII σ |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
σI |
|
σI σI |
|
|
σI σI |
|
|
σI |
|||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σII |
|
|
σIII |
|
σ |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
II |
|
|||
Рис. 9.3. Виды напряженного соcтояния
Линейное напряженное состояние — одно главное напряжение не равно нулю
(рис 9.3, а).
Примером линейного напряженного состояния являются растяжение-сжатие и чистый изгиб. При растяжении σ1 ≠ 0 , σ2 = σ3 = 0 . При сжатии σ3 ≠ 0 ,
σ1 = σ2 = 0 .
Плоское напряженное состояние — два главных напряжение не равны нулю
(рис. 9.3, б).
Примером плоского напряженного состояния являются сдвиг, изгиб и кручение длинных и тонких стержней, тонкостенные пластины и оболочки.
Объемное напряженное состояние — все три главных напряжения не равны нулю (рис. 9.3, в).
Примером объемного напряженного состояния является нагружение массивных тел.
Решение объемной задачи на порядок сложнее решения плоской задачи. Однако часто и для массивных тел можно использовать решения, найденные для плоского напряженного состояния.
Разрушение массивных тел чаще всего начинается с поверхности, а на поверхности одно из главных напряжений равно нулю. Следовательно вблизи поверхности можно использовать зависимости, полученные при плоском напряженном состоянии.
Кроме того, на практике часто встречаются частные случаи объемного напряженного состояния: плоское деформированное состояние и осесимметричное нагружение. для этих случаев используют уравнения плоского напряженного состояния с небольшой поправкой. Большинство расчетных программ, составленных для плоского напряженного состояния, как правило решают и задачи плоской деформации и осесимметричного нагружения.
9.4. Плоское напряженное состояние
К плоскому напряженному состоянию относятся большинство рассматриваемых в сопротивлении материалов случаев нагружения стержней, поэтому плоскому напряженному состоянию уделим особое внимание.
Найдем связь между напряжениями на гранях выделенного элемента и напряжениями на наклонной площадке. Рассмотрим прямую и обратную задачи.
9.4.1. Прямая задача
Предположим, что в какой-то точке тела известны главные напряжения σI ≠ 0 ,
σII ≠ 0 , σIII = 0 .
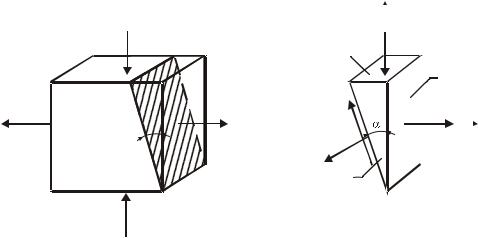
Требуется найти напряжения σα и τα на площадке, наклоненной под углом α к главной площадке (рис. 9.4, a).
|
|
|
|
|
|
y |
||||
а) |
σIII |
б) |
|
σIII |
||||||
|
Ay |
|
||||||||
|
|
|||||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||
|
σI |
|
|
|
|
|
|
Ax |
||
|
τα |
|
|
|
σI |
|||||
|
α? |
|
|
|
|
|
x |
|||
|
σα |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
Aα |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 9.4. Напряжения на наклонной площадке
Условимся, что знак касательного напряжения τ совпадает со знаком поперечной силы. Это не совпадает с правилом знаков для τ , принятым в теории упругости, но необходимо для построения круговой диаграммы Мора, о которой далее пойдет речь.
Расмотрим равновесие части выделенного элемента, отрезанного сечением под углом α (рис. 9.4, б). Спроектируем силы, действующие на отрезанную часть элемента на нормаль к наклонной площадке ν и на касательную к наклонной площадке ν + 90°
Площади граней рассматриваемой части элемента обозначим Aα , Ax , Ay .
∑Fα =σα Aα −σI AxCos(α) −σII Ay Sin(α) = 0 ,
∑Fν +90° =τα Aα −σI Ax Sin(α)+σII AyCos(α) = 0 .
С учетом |
Cos(α) = |
Αx |
и |
Sin(α) = |
Ay |
, |
|
||||||
|
|
A |
|
|
A |
|
|
|
α |
|
|
α |
|
Разделив оба выражения на Aα , получаем
σα =σICos2 (α)+σIISin2 (α) .
τα = (σI −σII )Sin(α)Cοs(α)
С учетом |
Sin(2α) = 2Sin(α)Cos(α) |
|
|
||||
Sin2 (α) = 1−Cos(2α) |
Cos2 |
(α) = |
1+ Cos(2α) |
получаем |
|||
|
|
2 |
|
|
2 |
|
|
σα = |
σI +σII + |
|
σI −σII |
Cos(2α) |
|
|
|
2 |
|
|
|
||||
|
2 |
|
|
|
(9.2). |
||
|
σI −σII Sin(2α) |
|
|
|
|||
τα = |
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
Уравнения (9.2) представляют собой параметрическое уравнение окружности типа
x= x0 + RCos(α).
y= y0 + Rsin(α)
Ввыражении (9.2)
σI −σII |
— радиус окружности, |
σI +σII |
— смещение центра окружности. |
2 |
|
2 |
|
Построим такую |
окружность в координатах σα −τα (рис. 9.5). Она называется |
||
круговая диаграмма Мора
Чтобы с помощью круга Мора определить напряжения на площадке, наклоненной на угол α , надо из центра круга провести луч под углом 2α и определить координаты σα ,τα точки пересечения луча с окружностью.
Примечание
Обратите внимание, что точки, соответствующие напряжениям на двух взаимноперпендикулярных площадках, лежат на одном диаметре.
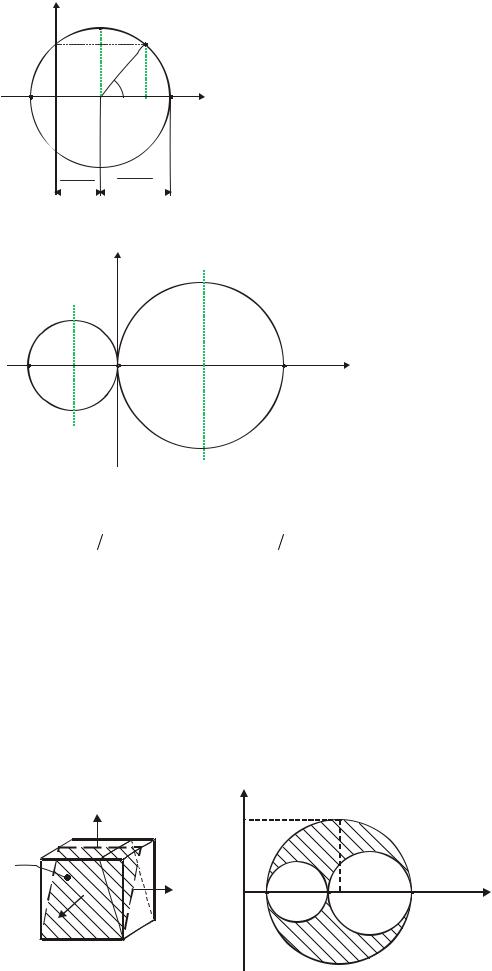
τα |
τ |
|
|
max |
|
|
|
(σα ,τα ) |
σIII |
2α |
σI σα |
σI +σIII
2
σI −σIII
2
Рис. 9.5. Круговая диаграмма Мора
В качестве примера построим круги Мора для растяжения и сжатия (рис.9.6).
τα
σIII |
|
|
|
σI |
σα |
|
0 |
|
|
|
|
сжатие |
|
|
|
|
|
|
|
|
растяжение |
|
|
Рис. 9.6. Круги Мора для растяжения и сжатия |
|
|
|||
При растяжении |
σI |
≠ 0 , |
σII =σIII = 0 . На оси σα |
отложить напряжение σI . |
|
Радиус круга σI |
2 . Смещение центра круга σI |
2 . Строим круг Мора. |
|||
При сжатии σIII |
≠ 0 , |
σI |
=σII = 0 . На оси σα |
отложить напряжение σIII . Радиус |
|
круга σIII  2 . Смещение центра круга σIII
2 . Смещение центра круга σIII  2 . Строим круг Мора.
2 . Строим круг Мора.
Круг Мора предназначен для определения напряжений при плоском напряженном состоянии, так как в построении используют напряжения на двух взаимно перпендикулярных площадках.
Для объемного напряженного состояния круг Мора можно применить для нахождения напряжений на площадках, параллельных одной из главных осей. В этом случае в построении круга будут участвовать напряжения только на двух площадках, как и при плоском напряженном состоянии.
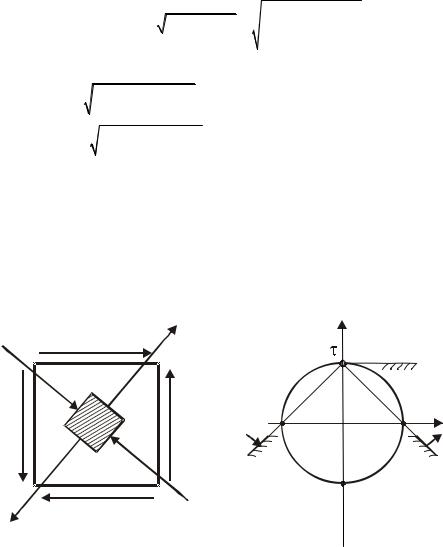
На рисунке 9.7, а изображен элемент, ориентированный по главным площадкам, при объемном напряженном состоянии.. Возьмем три плошадки, каждая из которых параллельна одной из главных осей, и построим для них круги Мора (рис.9.7, б).
|
σ |
|
|
τα |
τmax |
а) |
σ |
II |
б) |
|
|
|
|
|
II σ II
|
σ |
σ II |
σI =σmax |
0 |
III |
II |
|
σI |
|
|
σα |
σIII |
|
|
|
Рис. 9. 7. Круговая диаграмма Мора при объемном напряженном состоянии |
|
||
Если площадка параллельна напряжению σI , |
то в построении круга участвуют |
||
напряжения σII и σIII . Отложить на оси σα |
величины этих |
напряжений. Их |
|
разность — диаметр круга. Посередине — центр круга
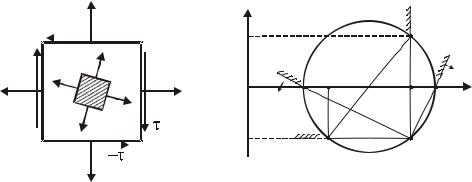
Аналогично строятся круги Мора для площадок, параллельных осям σII и σIII .
Точки, соответствующие напряженному состоянию произвольных площадок лежат в заштрихованной области между тремя кругами.
Анализируя круговую диаграмму Мора для объемного напряженного состояния сделаем важный для последующего изложения вывод о максимальных напряжениях в точке тела.
σ |
max |
=σ |
I |
τ |
max |
= |
σI −σIII |
|
|||||||
|
|
|
2 |
||||
|
|
|
|
|
|
||
Максимальные касательные напряжения всегда направлены под углом 45° к максимальным нормальным напряжениям.
9.4.2. Обратная задача
При плоском напряженном состоянии известны напряжения на гранях произвольно
выделенного |
элемента σx ,σ y ,τ |
(рис. 9.8, а). Требуется |
определить |
величину и |
||
направление главных напряжений σI ,σII ,σIII . |
|
|
|
|||
а) |
σ |
y |
б) τ |
|
|
|
|
|
α |
|
|
|
|
|
Б |
|
τ |
|
|
А |
|
|
|
|
|
|
|
|
|
А σx |
0 |
σy |
σx |
σα |
|
|
|
σII |
|
σI |
|
σII |
|
σI |
|
|
||
|
−τ |
|
|
|
||
|
|
|
Б |
|
Р |
|
|
|
|
|
|
||
Рис. 9.8. Обратная задача построения круга Мора
Построим круг Мора (рис. 9.8, б).
На площадке А действуют напряжения σx и τ .
На площадке Б действуют напряжения σ y и −τ .
В системе координат σα −τα отложим две точки, соответствующие напряженному состоянию на двух взаимно перепендикулярных площадках А и Б.
Эти две точки лежат на одном диаметре. Проведя прямую АБ, находим центр круга С на оси σα . Зная центр и радиус круга, проводим окружность. Точки пересечения
круга с осью σα дают величину главных напряжений σI и σIII .
Для определения направления главных напряжений через точки А и Б на окружности проведем прямые, параллельные площадкам А и Б до пересечения друг с другом. Точка пересечения Р лежит на окружности и называется полюсом круга.
Прямая, проведенная из полюса до любой точки окружности, будет параллельна площадке, напряженное состояние на которой соответствует точке пересечения с кругом.
Для наглядности по найденным направлениям внутри рассматриваемого элемента (рис. 9.8, а) построены главные площадки и показаны направления главных напряжений на них.
Прямые, проведенные из полюса до точек пересечения круга с осью σα , параллельны главным площадкам. Соответственно перпендикуляры к ним указывают направления главных напряжений σI и σIII на этих площадках.
Обратите внимание, что оси σα −τα необязательно должны быть параллельны граням выделенного элемента.
Наклоните выбранный элемент на некоторый угол. Поменяйте величину и направления действующих на него напряжений. Постройте для него круг Мора и определите величину и направление главных напряжений. Найдите напряжения на произвольно выбранной вами площадке или для любой точки круга найдите направление соответствующей ей площадки.
Рассмотренный метод определения направлений площадок и напряжений прост и элегантен, но...не очень важен. Круги Мора крайне редко используются в инженерной практике.
Воспользуемся кругом Мора, чтобы получить расчетную формулу для определения главных напряжений при плоском напряженном состоянии.
σI = OC + AC |
|
|
|
|
|
σIII = OC − AC , |
|
|
|
|
|
|
||||||
где OC = |
σx +σ y |
— смещение центра круга, АС — радиус круга. |
||||||||||||||||
|
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
x |
−σ |
y |
2 |
По теореме Пифагора AC = CD2 + AD2 = |
|
|
|
+τ2 . |
||||||||||||||
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончательно |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
σI = |
σx +σ y |
+ |
1 |
|
|
(σx −σ y )2 + 4τ2 |
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
(9.3). |
||||||
|
|
σx +σ y |
|
|
|
1 |
(σx −σ y )2 + 4τ2 |
|
|
|
|
|
||||||
σIII = |
|
− |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||
Направление главных напряжений αглав |
определим через тангенс двойного угла |
||||||
tg(2αглав ) = |
AD |
= |
|
2τ |
|
(9.4). |
|
CD |
σx −σ y |
||||||
|
|
|
|||||
В качестве примера рассмотрим определение главных напряжений при чистом сдвиге
(рис. 9.9).
τ |
|
σI |
|
τa |
σIII |
|
|
P |
Б |
Б |
|
|
|
|
−τ |
А |
−τ |
σIII |
σI σα |
|
|
|
||
τ |
|
|
−τ |
А |
|
|
|
|
Рис. 9.9. Круг Мора при чистом сдвиге
На площадке А действуют напряжения σ = 0 и τ .
На площадке Б действуют σ = 0 и −τ . Строим круг Мора, по которому определяем главные напряжения σI =τ и σIII = −τ .
9.5 Связь напряжений и деформаций. Обобщенный закон Гука
В предыдущих главах уже рассматривалась связь напряжений и деформаций при простых видах упругой деформации. Пришло время установить такую связь в общем случае нагружения. Напомним закон Гука при растяжении и при сдвиге
При растяжении (рис. 9.10, а) |
σx = E εx . |
|
|
||
В продольном направлении |
εx = |
σx |
. |
|
|
|
|
|
|||
|
|
E |
|
|
|
В поперечном направлении |
εy =εz = −μεx = −μ |
σx |
. |
||
|
|||||
|
|
|
|
E |
|
Следует отметить, что линейная деформация не вызывает сдвига. Прямые углы в растянутом элементе остаются прямыми.
При сдвиге (рис. 9.10, б) |
|
τxy = G γ xy . |
||
Откуда угол сдвига |
γ xy = |
τxy |
. |
|
G |
||||
|
|
|
||
