Остальные характеристики определить невозможно. Характеристики пластичности у материалов в хрупком состоянии, как показывают замеры образцов до и после разрушения, близки к нулю.
5.3 Испытание материалов на сжатие
Испытание материалов на растяжение — основной вид испытаний материалов. Именно результаты испытаний на растяжение приводятся во всех справочниках как механические характеристики материалов.
Все другие виды испытаний являются технологическими и проводятся только в случае производственной необходимости. Тем не менее их изучение позволяет изучить поведение материалов при различных видах напряженно-деформированного состояния.
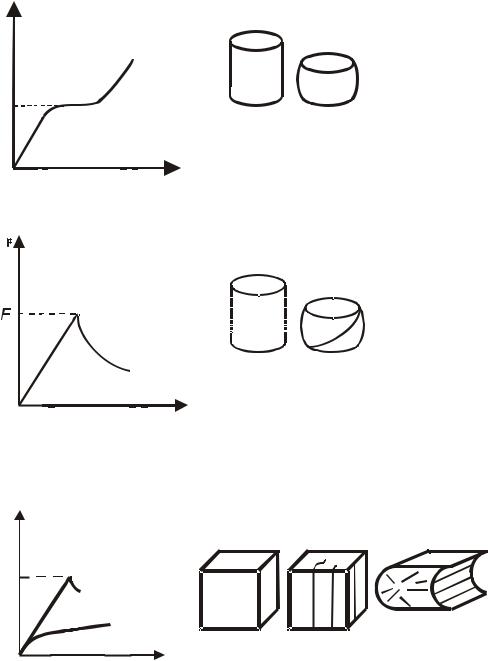
При сжатии образцов из мягкой стали и других высокопластичных материалов разрушения получить не удается.
Поскольку объем образца при пластической деформации не меняется, с уменьшением высоты образца при сжатии площадь поперечного сечения увеличивается. Соответственно растет нагрузка, вызывающая пластическую деформацию. Диаграмма сжатия стали и вид образца до и после испытания показаны на рис. 5.5.
F
FT
L
Рис. 5.5. Испытание стали на сжатие
в
L
Рис. 5.6. Испытание чугуна на сжатие
F
FB
L
до после
деформации
До После Деформации
Вдоль Поперек Волокон
До После Деформации
Рис. 5. 7. Испытание дерева на сжатие
Поведение чугуна при сжатии резко отличается от его поведения при растяжении. Если для испытаний на растяжение используется образец, у которого h
d = 10 , то
для испытаний на сжатие берут h
d = 1, 5 , так как при сжатии более длинного
образца при больших нагрузках возможна потеря устойчивости образца, то есть изгиб его в боковом направлении. Вид чугунного образца до и после испытаний и его диаграмма сжатия показаны на рис. 5.6.
Цилиндрический образец (и стальной и чугунный) при сжатии превращается в бочонок. При этом его высота значительно меньше, чем до испытаний, то есть налицо большая пластическая деформация чугунного образца.
Бочкообразная форма образца вызвана силами трения между образцом и поверхностью пресса. Если уменьшить трение путем смазки торцов образца, например, парафином, то бочкообразность практически исчезает. Иногда для ее устранения используют тонкие медные прокладки толщиной 0,1мм, но при этом бочка может превратиться в рюмку.
Если стальной образец при сжатии не разрушается вовсе, то чугунный разрушается путем скола (среза) под углом порядка 30° к оси образца, а если уменьшить силу трения смазкой, то угол плоскости среза приближается к 45°. Следовательно при сжатии чугуна разрушение происходит путем среза под действием максимальных касательных напряжений. Напомню, при растяжении-сжатии плоскость действия максимальных касательных напряжений наклонена под углом 45° к оси стержня.
В изломе образца хорошо видны следы сдвига. Таким образом при сжатии чугунного образца наблюдаются все признаки пластического разрушения.
При растяжении чугун разрушается хрупко, при сжатии пластично. Более подробно об условиях перехода от пластического разрушения к хрупкому написано в главе 16.
Важно отметить, что прочность чугуна на сжатие в 4 раза больше, чем на растяжение. Сталь при сжатии не разрушается, а вот пределы пропорциональности и текучести при растяжении и при сжатии примерно одинаковы.
Примером хрупкого разрушения при сжатии может служить сжатие камня, бетона, стали после закалки без отпуска, дерева вдоль волокон. В этих случаях разрушение происходит по плоскостям параллельным оси образца путем расслоения образца на отдельные сегменты.
Причиной разрушения при этом является не σmax или τmax , а максимальная линейная деформация εmax . Речь о ней пойдет в разделе 9.6.
Отдельного рассмотрения заслуживает сжатие дерева. Дерево анизотропный материал, у которого свойства вдоль волокон и поперек волокон различны. вид образцов до и после испытаний и диаграммы сжатия дерева вдоль и поперек волокон показаны на рис. 5.7.
Предел прочности дерева на растяжение примерно в два раза больше, чем на сжатие. Это объясняется тем, что при сжатии вдоль волокон дерево разрушается хрупко. Оно расслаивается на отдельные волокна, которые при дальнейшей деформации теряют устойчивость, изгибаются и переламываются.
При сжатии поперек волокон дерево деформируется пластично. Волокна сдвигаются друг относительно друга, образец сплющивается и в конце концов разваливается в силу недостаточной прочности скрепления волокон. Предел прочности дерева вдоль волокон примерно в 10 раз больше, чем поперек волокон.
5.4 Допускаемые напряжения
Понятие о допускаемом напряжении уже давалось в разделе 1.10. Пришло время уточнить, что принять в качестве предельного напряжения.
При расчете конструкции на прочность и жесткость будем рассматривать два вида выхода конструкции из строя:
разделение тела на части (хрупкое разрушение),
Появление недопустимых пластических деформаций (пластическая деформация, но не разрушение).
В реальных условиях существует и много других видов выхода из строя, например, потеря устойчивости, износ, коррозия и др.
При расчетах на прочность условие выхода конструкции из строя σmax = σпред .
Условие работоспособности конструкции σmax = [σ].
Допускаемое напряжение |
[σ] = |
σпред |
, где |
|
n |
||||
|
|
|
•σпред = σв — для материалов в хрупком состоянии
•σпред = σт — для материалов в пластичном состоянии.
Коэффициент запаса n выбирается по справочникам в зависимости от условий эксплуатации конструкции и других факторов. Перечислим основные факторы, учитываемые при выборе коэффициента запаса.
Точность знания нагрузок и их характера. Точность расчетных формул. Возможные последствия выхода из строя.
Коэффициент запаса иногда называют еще коэффициент незнания. Чем меньше мы знаем, тем больше коэффициент запаса.
Если рассчитывается неответственная деталь, которую в случае поломки легко заменить, коэффициент запаса можно взять минимальным n = 1, 2 −1, 5 .
Если возможная поломка может вызвать гибель людей, например, трос подъема лифта, коэффициент запаса берется максимально большим n = 10 −15 .
Коэффициент запаса косвенным образом оценивает возможную вероятность выхода из строя конструкции, как сказано в разделе 1.13.3.
5.5 Диаграммы условных и истинных
напряжений
В процессе испытаний изменяется площадь поперечного сечения образца. При подсчете напряжений в образце изменение площади сечения можно учитывать или не учитывать, получая соответственно условные или истинные напряжения
До образования шейки деформация по всей длине образца одинаковая. В процессе образования шейки деформация происходит только в области шейки.
Диаметр шейки уменьшается, диаметр остальной части образца не меняется.. Соответственно деформации образца можно определять с учетом и без учета изменения диаметра, получая при этом условные или истинные деформации.
Условными называются напряжения, найденные как отношение нагрузки к
первоначальной площади поперечного сечения σусл = |
F |
. |
|
||
|
A0 |
|
Условными называются деформации, найденные как отношение удлинения образца к
его первоначальной длине |
ε = |
L . |
|
|
L |
|
|
0 |
Истинными называются напряжения, найденные как отношение нагрузки к текущей
площади поперечного сечения σист = |
F |
. |
|
||
|
Aист |
|
Истинными называются деформации, найденные как отношение приращение длины элемента образца к текущей длине этого элемента.
Чтобы определить истинные напряжения необходимо в процессе испытаний замерять диаметр образца в области шейки, что обычно не делается, а замеряется лишь диаметр шейки после разрыва.
Ввести понятие истинной деформации не так просто, ведь надо оценить деформации в шейке, которая образуется неизвестно где.
Рассмотрим элемент образца длиной dL0 до деформации. В произвольный момент
нагружения |
его |
длина |
становится равной |
dL . Дадим небольшое приращение |
||||||
нагрузки, длина элемента вырастет еще на |
d(dL) |
(рис. 5.8). Тогда приращение |
||||||||
деформации |
элемента |
dεист |
= |
d(dL) |
, а полная |
истинная деформация за все |
||||
|
||||||||||
нагружение |
|
|
|
|
|
|
dL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dL |
|
d(dL) |
|
dL |
|
|
|
|
|
εист = ∫ |
|
|
= ln |
|
. |
|
|
|
||
|
dL |
dL |
|
|
|
|||||
|
dL |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Поскольку отношение приращений длины неизвестно, выразим его через известные величины.
d0 |
d |
|
|
dL0
dL |
d(dL) |
|
|
|
|
Рис. 5.8. К расчету истинных деформаций при растяжении
Пластическая деформация протекает без изменением объема пренебрегаем. Считаем постоянным.
dV = A0dL0 = AdL , |
откуда |
изменения объема тела. Упругим объем тела в процессе деформации
dL = A0 , dL0 A
|
dL |
|
|
A |
|
тогда εист = ln |
|
|
= ln |
0 |
. |
|
A |
||||
dL0 |
|
|
|
||
Чтобы найти истинную деформацию в момент разрыва надо знать площадь шейки при разрыве или при использовании справочных данных можно взять относительное сужение ψ в момент разрыва
ψ = |
A0 − Aк |
=1 |
− |
Aк |
|
или |
|
A0 |
= |
|
|
1 |
, тогда |
||||||
|
|
|
A |
1 |
−ψ |
||||||||||||||
|
A |
|
|
|
|
|
A |
0 |
|
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
||
|
|
|
dL |
|
|
|
|
A |
|
|
1 |
|
|
|
|
|
|
||
εист = ln |
|
|
|
|
= ln |
|
0 |
|
= ln |
|
|
|
. |
|
|
||||
|
|
A |
|
|
|
|
|
||||||||||||
|
|
dL0 |
|
|
|
|
|
|
1−ψ |
|
|
|
|
||||||
Для пластичных сталей ψ ≈ 0,6 – 0,7 и ε ≈1, то есть деформация в шейке достигает
100%.
Свяжем истинные деформации εист и истинные напряжения σист .
σ |
|
= |
F |
= |
F |
|
A0 |
=σ |
|
A0 |
=σ |
|
eεист . |
ист |
A |
A |
A |
усл A |
усл |
||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
До образования шейки — деформация одинаковая по всей длине образца, тогда из условия постоянства объема образца
A L = AL , |
A0 |
= |
L |
= |
L0 + L |
=1+ε |
усл |
, |
|
|
|
||||||
0 0 |
A |
|
L0 |
|
L0 |
|
||
|
|
|
|
|
||||
εист = ln A0 = ln(1+εусл) ≈ εусл ,
A
σист =σуслeln(1+εист ) =σусл(1+εист)
Построение диаграммы истинных напряжений, выполненное в Mathcad, приведено в электронной книге в единственном примере главы 5.
Рис. 5.9. Сопоставление диаграмм условных и истинных напряжений
Диаграммы условных и истинных напряжений, полученные в указанном примере показаны на рис. 5.9. Диаграмма условных напряжений σусл – εусл подобна
диаграмме деформирования, нарисованной машиной в координатах нагрузка – удлинение ( F – L ). Действительно условные напряжения и деформация — это нагрузка и удлинение, деленные на постоянную величину, то есть фактически просто изменен масштаб диаграммы деформирования.
Диаграмма истинных напряжений в 5 – 7 раз длиннее и в 2 – 3 раза выше диаграммы условных напряжений.
В практических расчетах на прочность при необходимости учета пластических деформаций используются различные аппроксимации диаграммы деформирования. Используемые виды аппроксимации диаграммы деформирования описаны в разделе 8.2.