Рис. 33. Операции с матрицами

Решение матричных уравнений

Матричные уравнения представляют собой, как правило, систему линейных алгебраических уравнений A · X = B и решаются путем обращения матрицы коэффициентов X = A-1 · B (рис. 34).

Рис. 34. Решение системы алгебраических линейных уравнений путем обращения матрицы коэффициентов

Символьные операции с матрицами можно производить с помощью меню Symbolics и с помощью символьного знака равенства. В примерах на рис. 35 используется только символьный знак равенства →. Подробно о символьных операциях с матрицами рассказано в электронной книге в разделе Символьные вычисления).

При выполнении символьных операций с матрицами необходимо помнить, что если какому-либо символу ранее присвоено численное значение, то при использовании символьного знака равенства этот символ участвует в символьных расчетах как число. Если символу ранее присвоено значение вектора или матрицы, то символьные вычисления с его участием становятся невозможными. В этих случаях надо использовать для символьных вычислений меню Symbolics.

Оператор векторизации

Mathcad допускает в качестве аргумента функции вводить не только числа, но и векторы. При этом вычисляется значение функции для всех элементов вектора. Если аргумент функции — матрица, то, чтобы вычислить значения функции для всех элементов матрицы, надо использовать оператор векторизации (рис. 36).

Рис. 35. Символьные операции с матрицами

Для использования оператора векторизации надо:

ввести выражение или функцию;

выделить синим уголком необходимую часть выражения (чаще всего выражение целиком);

на математической панели щелкнуть на кнопке Vector and Matrix Toolbar, а в

JJJJJJG

открывшейся панели — кнопке Vectorize ( f (M) ) (Векторизация). Над

выделенной частью выражения появится стрелка — символ операции векторизации;

нажать клавишу =.

Оператор векторизации изменяет смысл векторной или матричной операции. Векторизация означает выполнение однотипной операции, предписанной

выражением, со всеми элементами массива. Например, A — операция невозможная, если A — вектор или матрица.

Рис. 36. Операция векторизации в Mathcad

Начиная с версии Mathcad 2000, аргумент функции может быть вектором, и функция, как и в случае использования дискретной переменной, вычисляется для всех элементов вектора.

Если аргумент функции — матрица, необходимо применение оператора векторизации, чтобы выполнить то же самое, то есть вычислить функцию для всех элементов матрицы. В нашем случае это корень квадратный из каждого элемента

матрицы A. В случае перемножения матриц A B это матричное произведение, а

JJJJJG

A B — это попарное произведение элементов матриц A и B с одинаковыми индексами. Все массивы под знаком векторизации должны быть одного размера, так как операция над всеми массивами производится поэлементно. Использование векторов или матриц в качестве аргументов функции приведены на рис. 36.

ВНИМАНИЕ

Если аргумент — вектор, векторизация не нужна. Если аргумент — матрица, векторизация нужна.

Решение дифференциальных уравнений

Математически решение дифференциальных уравнений — очень сложная проблема. Mathcad не в состоянии решить без дополнительных упрощений многие дифференциальные уравнения и их системы. Все, что Mathcad может сделать с ними, подробно описано в электронной книге в разделе Решение дифференциальных уравнений. Здесь рассмотрим лишь использование одной функции odesolve. Имя функции odesolve можно писать и с прописной, и со строчной буквы. Алгоритм функции odesolve использует большинство, имеющихся в Mathcad функций решения дифференциальных уравнений, фактически заменяя их. Эта замечательная функция появилась в Mathcad 2000 и могла решить лишь одно дифференциальное уравнение.

ВMathcad 2001i возможности этой функции расширены. Теперь odesolve может решать и системы дифференциальных уравнений. В последующих версиях Mathcad устранен ряд ошибок, возникавших при использовании этой функции. В контекстном меню появилась возможность выбора метода решения дифференциальных уравнений.

ВMathcad много встроенных функций для решения дифференциальных уравнений. Все они, кроме функции odesolve, требуют определенной, непростой формы записи исходного уравнения. Функция odesolve позволяет записывать уравнение в блоке решения в привычном виде, как обычно записывают уравнение на листе бумаги.

Рис. 37. Решение дифференциального уравнения с начальными условиями

Обращение к функции odesolve требует записи вычислительного блока, состоящего

из трех частей:

1.ключевое слово given;

2.дифференциальное уравнение и начальные или граничные условия к нему, или система дифференциальных уравнений и условия к ней;

3.функция odesolve(x, xk, n), где

x — имя переменной, относительно которой решается уравнение;

xk — конец интервала интегрирования. Начало интервала интегрирования указано выше в начальных условиях;

n — необязательный внутренний параметр, определяющий число шагов интегрирования, на которых вычисляется решение дифференциального уравнения.

Чем больше n, тем с большей точностью будет решено уравнение, тем больше будет время решения. Параметр n не является обязательным. Его можно удалить, предоставив Mathcad возможность самому выбирать число шагов интегрирования.

ВНИМАНИЕ

Появление других математических выражений в вычислительном блоке между словами given и odesolve недопустимо. Текстовую область внутри вычислительного блока размещать можно. Граничные условия можно задавать лишь в двух точках, одна из которых — начало интервала интегрирования.

Примеры использования функции odesolve приведены на рис. 37 – 40.

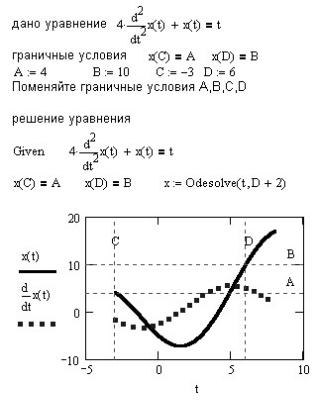
Рис. 38. Решение дифференциального уравнения с граничными условиями

ПРИМЕЧАНИЕ

Исходное уравнение можно записывать как с использованием оператора дифференцирования, так и со штрихом (рис. 39). Граничные условия следует записывать только со штрихом. Для набора штриха используйте сочетание клавиш

Ctrl+F7.

Функция odesolve возвращает решение дифференциального уравнения в виде функции, а не в виде массива, как все остальные функции решения дифференциальных уравнений, поэтому найденное решение можно интегрировать и