
Киреев - Расчёт И Проектирование Зуборезных Инструментов
.pdfРАСЧЕТ И ПРОЕКТИРОВАНИЕ
ЗУБОРЕЗНЫХ ИНСТРУМЕНТОВ
Прудников
Киреев
ȼȼȿȾȿɇɂȿ
Ʉ ɱɢɫɥɭ ɧɚɢɛɨɥɟɟ ɫɥɨɠɧɵɯ ɢ ɞɨɪɨɝɢɯ ɦɟɬɚɥɥɨɪɟɠɭɳɢɯ ɢɧɫɬɪɭɦɟɧɬɨɜ ɨɬɧɨ-
ɫɹɬɫɹ ɡɭɛɨɪɟɡɧɵɟ ɢɧɫɬɪɭɦɟɧɬɵ. ȼ ɩɨɫɨɛɢɢ ɩɪɢɜɟɞɟɧɵ ɦɟɬɨɞɵ ɪɚɫɱɟɬɚ ɢ ɩɪɨɟɤɬɢ-
ɪɨɜɚɧɢɹ ɢɧɫɬɪɭɦɟɧɬɨɜ ɞɥɹ ɨɛɪɚɛɨɬɤɢ ɡɭɛɱɚɬɵɯ ɤɨɥɟɫ ɫ ɷɜɨɥɶɜɟɧɬɧɵɦ ɩɪɨɮɢɥɟɦ ɡɭɛɶɟɜ ɜɧɟɲɧɟɝɨ ɡɚɰɟɩɥɟɧɢɹ ɢ ɲɥɢɰɟɜɵɯ ɜɚɥɨɜ ɫ ɷɜɨɥɶɜɟɧɬɧɵɦ ɢ ɩɪɹɦɨɥɢɧɟɣɧɵɦ ɩɪɨɮɢɥɟɦ ɡɭɛɶɟɜ. ɇɚɢɛɨɥɶɲɭɸ ɩɪɨɢɡɜɨɞɢɬɟɥɶɧɨɫɬɶ ɢ ɬɨɱɧɨɫɬɶ ɨɛɪɚɛɨɬɤɢ ɬɚɤɨɝɨ ɬɢɩɚ ɢɡɞɟɥɢɣ ɨɛɟɫɩɟɱɢɜɚɸɬ ɢɧɫɬɪɭɦɟɧɬɵ, ɪɚɛɨɬɚɸɳɢɟ ɩɨ ɦɟɬɨɞɭ ɰɟɧɬɪɨɢɞɧɨɝɨ ɨɝɢɛɚɧɢɹ - ɨɛɤɚɬɚ. ɂɦɟɧɧɨ ɞɥɹ ɬɚɤɨɝɨ ɬɢɩɚ ɢɧɫɬɪɭɦɟɧɬɨɜ ɪɚɫɫɦɨɬɪɟɧɵ ɫɩɨɫɨɛɵ ɪɚɫɱɟɬɚ ɢ ɩɪɨɟɤɬɢɪɨɜɚɧɢɹ.
ȼ ɭɫɥɨɜɢɹɯ ɦɚɫɫɨɜɨɝɨ ɩɪɨɢɡɜɨɞɫɬɜɚ ɡɭɛɱɚɬɵɯ ɤɨɥɟɫ ɢ ɲɥɢɰɟɜɵɯ ɜɚɥɨɜ, ɧɚ-
ɩɪɢɦɟɪ, ɜ ɚɜɬɨɦɨɛɢɥɟɫɬɪɨɟɧɢɢ, ɢɫɩɨɥɶɡɭɸɬɫɹ ɫɩɟɰɢɚɥɶɧɵɟ ɪɟɠɭɳɢɟ ɢɧɫɬɪɭɦɟɧɬɵ.
ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɡɭɛɨɪɟɡɧɵɣ ɢɧɫɬɪɭɦɟɧɬ ɩɪɨɟɤɬɢɪɭɟɬɫɹ ɞɥɹ ɨɛɤɚɬɤɢ ɡɭɛɱɚɬɨɝɨ ɤɨɥɟɫɚ ɬɨɥɶɤɨ ɫ ɨɩɪɟɞɟɥɟɧɧɵɦ ɱɢɫɥɨɦ ɡɭɛɶɟɜ, ɚ ɲɥɢɰɟɜɨɝɨ ɜɚɥɚ ɫ ɨɩɪɟɞɟɥɟɧɧɵɦ ɱɢɫɥɨɦ ɲɥɢɰɟɜ ɢ ɞɪɭɝɢɦɢ ɤɨɧɤɪɟɬɧɵɦɢ ɩɚɪɚɦɟɬɪɚɦɢ. ȼ ɩɨɫɨɛɢɢ ɧɟ ɪɚɫɫɦɚɬɪɢɜɚɸɬɫɹ ɪɚɫ-
ɱɟɬɵ, ɫɜɹɡɚɧɧɵɟ ɫ ɜɨɡɦɨɠɧɨɫɬɶɸ ɩɪɢɦɟɧɟɧɢɹ ɫɬɚɧɞɚɪɬɧɨɝɨ ɢɧɫɬɪɭɦɟɧɬɚ ɞɥɹ ɨɛɪɚ-
ɛɨɬɤɢ ɡɭɛɱɚɬɵɯ ɤɨɥɟɫ ɢ ɲɥɢɰɟɜɵɯ ɜɚɥɨɜ.
Ɉɩɬɢɦɚɥɶɧɨɣ ɤɨɧɫɬɪɭɤɰɢɟɣ ɡɭɛɨɪɟɡɧɨɝɨ ɢɧɫɬɪɭɦɟɧɬɚ ɹɜɥɹɟɬɫɹ ɬɚɤɚɹ ɤɨɧɫɬ-
ɪɭɤɰɢɹ, ɤɨɬɨɪɚɹ ɩɪɢ ɩɪɢɦɟɧɟɧɢɢ ɢɧɫɬɪɭɦɟɧɬɚ ɨɛɟɫɩɟɱɢɜɚɟɬ ɧɚɢɦɟɧɶɲɢɟ ɡɚɬɪɚɬɵ ɩɨ ɟɝɨ ɷɤɫɩɥɭɚɬɚɰɢɢ ɩɪɢ ɢɡɝɨɬɨɜɥɟɧɢɢ ɨɞɧɨɝɨ ɡɭɛɱɚɬɨɝɨ ɤɨɥɟɫɚ. ɉɪɢ ɷɬɨɦ ɬɚɤɨɣ ɢɧɫɬɪɭɦɟɧɬ ɞɨɥɠɟɧ ɨɛɟɫɩɟɱɢɜɚɬɶ ɬɪɟɛɭɟɦɨɟ ɤɚɱɟɫɬɜɨ - ɬɨɱɧɨɫɬɶ ɡɭɛɱɚɬɵɯ ɤɨɥɟɫ ɢ ɲɟɪɨɯɨɜɚɬɨɫɬɶ ɩɨɜɟɪɯɧɨɫɬɢ ɡɭɛɶɟɜ. ɉɨɞɯɨɞ ɤ ɨɩɬɢɦɢɡɚɰɢɢ ɤɨɧɫɬɪɭɤɰɢɢ ɡɭɛɨɪɟɡ-
ɧɨɝɨ ɢɧɫɬɪɭɦɟɧɬɚ ɬɚɤɠɟ ɪɚɫɫɦɨɬɪɟɧ ɜ ɭɱɟɛɧɨɦ ɩɨɫɨɛɢɢ. Ɋɟɲɟɧɢɟ ɜɨɩɪɨɫɚ ɨɩɬɢɦɢ-
ɡɚɰɢɢ ɤɨɧɫɬɪɭɤɰɢɢ, ɤɚɤ ɩɪɚɜɢɥɨ, ɭɫɩɟɲɧɨ ɦɨɠɟɬ ɛɵɬɶ ɜɵɩɨɥɧɟɧɨ ɩɪɢ ɩɪɨɟɤɬɢɪɨ-
ɜɚɧɢɢ ɫ ɩɨɦɨɳɶɸ ɗȼɆ.
Ɍɨɱɧɨɫɬɶ ɩɚɪɚɦɟɬɪɨɜ ɡɭɛɨɪɟɡɧɵɯ ɢɧɫɬɪɭɦɟɧɬɨɜ ɨɩɪɟɞɟɥɹɟɬɫɹ ɪɟɲɟɧɢɟɦ ɬɪɚɧɫɰɟɧɞɟɧɬɧɵɯ ɭɪɚɜɧɟɧɢɣ. Ⱦɚɧ ɚɥɝɨɪɢɬɦ ɪɟɲɟɧɢɹ ɬɚɤɢɯ ɭɪɚɜɧɟɧɢɣ ɧɚ ɗȼɆ.
ȼ ɫɜɹɡɢ ɫ ɧɟɞɨɫɬɚɬɨɱɧɨɫɬɶɸ ɢɥɢ ɩɨɥɧɵɦ ɨɬɫɭɬɫɬɜɢɟɦ ɫɬɚɧɞɚɪɬɨɜ ɧɚ ɡɭɛɱɚɬɵɟ ɤɨɥɟɫɚ, ɲɥɢɰɟɜɵɟ ɜɚɥɵ ɢ ɡɭɛɨɪɟɡɧɵɟ ɢɧɫɬɪɭɦɟɧɬɵ ɜ ɛɢɛɥɢɨɬɟɤɟ ɜɭɡɚ, ɜ ɩɨɫɨɛɢɢ ɞɚɧɵ ɧɟɤɨɬɨɪɵɟ ɦɚɬɟɪɢɚɥɵ, ɤɨɬɨɪɵɟ ɨɛɥɟɝɱɚɬ ɩɪɨɰɟɫɫ ɪɚɫɱɟɬɚ ɢ ɩɪɨɟɤɬɢɪɨɜɚɧɢɹ ɡɭɛɨɪɟɡɧɨɝɨ ɢɧɫɬɪɭɦɟɧɬɚ, ɩɪɢɜɟɞɟɧɵ ɩɪɢɦɟɪɵ ɪɚɫɱɟɬɚ ɢ ɪɚɛɨɱɢɯ ɱɟɪɬɟɠɟɣ ɦɨɧɨ-
ɥɢɬɧɨɝɨ ɡɭɛɨɪɟɡɧɨɝɨ ɢɧɫɬɪɭɦɟɧɬɚ.
5
. ɂɋɏɈȾɇɕȿ ȾȺɇɇɕȿ, ɋɉɊȺȼɈɑɇȺə ɂɇɎɈɊɆȺɐɂə ȾɅə ɉɊɈȿɄɌɂɊɈȼȺɇɂə ɁɍȻɈɊȿɁɇɕɏ ɂɇɋɌɊɍɆȿɇɌɈȼ ɂ ɊȺɋɑȿɌ ȾɈɉɈɅɇɂɌȿɅɖɇɕɏ ɌȿɏɇɈɅɈȽɂɑȿɋɄɂɏ ɉȺɊȺɆȿɌɊɈȼ ɁɍȻɑȺɌɕɏ ɄɈɅȿɋ ɂ ɒɅɂɐȿȼɕɏ ȼȺɅɈȼ
ȼ ɡɚɞɚɧɢɢ ɧɚ ɤɭɪɫɨɜɨɟ ɢɥɢ ɞɢɩɥɨɦɧɨɟ ɩɪɨɟɤɬɢɪɨɜɚɧɢɟ ɜ ɤɚɱɟɫɬɜɟ ɢɫ-
ɯɨɞɧɵɯ ɞɚɧɧɵɯ ɩɪɢɜɨɞɹɬɫɹ ɩɚɪɚɦɟɬɪɵ ɨɛɪɚɛɚɬɵɜɚɟɦɨɝɨ ɢ ɫɨɩɪɹɠɟɧɧɨɝɨ ɤɨ-
ɥɟɫ ɡɭɛɱɚɬɨɣ ɩɚɪɵ: ɱɢɫɥɨ ɡɭɛɶɟɜ ɨɛɪɚɛɚɬɵɜɚɟɦɨɝɨ z1 ɢ ɫɨɩɪɹɠɟɧɧɨɝɨ z2 ɤɨ-
ɥɟɫ; ɦɨɞɭɥɶ m; ɭɝɨɥ ɩɪɨɮɢɥɹ ɧɚ ɞɟɥɢɬɟɥɶɧɨɦ ɞɢɚɦɟɬɪɟ α; ɤɨɷɮɮɢɰɢɟɧɬ ɜɵ-
ɫɨɬɵ ɝɨɥɨɜɤɢ ɡɭɛɚ ha* ; ɝɪɚɧɢɱɧɨɣ ɜɵɫɨɬɵ ɡɭɛɚ hl* ɢ ɧɨɠɤɢ ɡɭɛɚ h*f ; ɭɝɨɥ ɧɚ-
ɤɥɨɧɚ ɡɭɛɶɟɜ β; ɤɨɷɮɮɢɰɢɟɧɬɵ ɤɨɪɪɟɤɰɢɢ ɡɭɛɱɚɬɵɯ ɤɨɥɟɫ x ɢ x2 (ɢɥɢ ɬɨɥɳɢ-
ɧɚ ɡɭɛɶɟɜ ɤɨɥɟɫ ɜ ɧɨɪɦɚɥɶɧɨɦ ɫɟɱɟɧɢɢ ɧɚ ɞɟɥɢɬɟɥɶɧɨɣ ɨɤɪɭɠɧɨɫɬɢ Sn1 ɢ Sn2);
ɫɬɟɩɟɧɶ ɬɨɱɧɨɫɬɢ ɩɚɪɵ ɡɭɛɱɚɬɵɯ ɤɨɥɟɫ ɩɨ ɜɫɟɦ ɧɨɪɦɚɦ ɬɨɱɧɨɫɬɢ, ɜɢɞ ɫɨɩɪɹ-
ɠɟɧɢɹ ɩɨ ȽɈɋɌ 643-8 . Ɇɨɠɟɬ ɛɵɬɶ ɭɤɚɡɚɧɢɟ ɨɛ ɨɛɨɪɭɞɨɜɚɧɢɢ (ɦɨɞɟɥɶ ɫɬɚɧɤɚ), ɧɚ ɤɨɬɨɪɨɦ ɞɨɥɠɧɚ ɜɵɩɨɥɧɹɬɶɫɹ ɨɛɪɚɛɨɬɤɚ ɡɭɛɱɚɬɨɝɨ ɤɨɥɟɫɚ. Ⱦɥɹ ɪɚɫɱɟɬɚ ɩɚɪɚɦɟɬɪɨɜ ɡɭɛɨɪɟɡɧɵɯ ɢɧɫɬɪɭɦɟɧɬɨɜ ɧɟɨɛɯɨɞɢɦɨ ɨɩɪɟɞɟɥɹɬɶ ɞɨ-
ɩɨɥɧɢɬɟɥɶɧɵɟ ɬɟɯɧɨɥɨɝɢɱɟɫɤɢɟ ɩɚɪɚɦɟɬɪɵ ɡɭɛɱɚɬɵɯ ɤɨɥɟɫ.
Ⱦɢɚɦɟɬɪɵ ɞɟɥɢɬɟɥɶɧɵɯ ɨɤɪɭɠɧɨɫɬɟɣ
d = |
mz |
; d |
|
= |
mz 2 |
. |
( . ) |
|
|
||||||
cos β |
|
||||||
|
|
2 |
|
cos β |
|
||
ɍɝɨɥ ɩɪɨɮɢɥɹ ɢ ɦɨɞɭɥɶ ɩɨ ɬɨɪɰɭ (ɬɨɪɰɨɜɵɣ ɩɪɨɮɢɥɶɧɵɣ ɭɝɨɥ ɢ ɬɨɪɰɨ-
ɜɵɣ ɦɨɞɭɥɶ)
d |
t |
= arctg |
tg α |
|
|
; m |
t |
|
= |
m |
|
; |
( .2) |
|||
|
|
cos β |
|
|
|
|
|
cos β |
|
|||||||
ɞɥɹ ɩɪɹɦɨɡɭɛɵɯ ɤɨɥɟɫ α |
t |
=α |
ɢ m |
= m. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
Ⱦɢɚɦɟɬɪɵ ɨɫɧɨɜɧɵɯ ɨɤɪɭɠɧɨɫɬɟɣ |
|
|||||||||||||||
d |
b |
=d cosα |
; d |
b |
= d |
2 |
cosα ; |
( .3) |
||||||||
|
|
t |
|
|
|
|
|
t |
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
6

ɍɝɨɥ ɡɚɰɟɩɥɟɧɢɹ ɜ ɩɟɪɟɞɚɱɟ ɩɨ ɬɨɪɰɭ ɤɨɥɟɫ αtw ɡɚɜɢɫɢɬ ɨɬ ɬɨɝɨ, ɢɡɜɟɫɬɧɨ ɢɥɢ ɧɟɢɡɜɟɫɬɧɨ ɦɟɠɨɫɟɜɨɟ ɪɚɫɫɬɨɹɧɢɟ αw .
ɉɪɢ ɧɟɡɚɞɚɧɧɨɦ ɦɟɠɨɫɟɜɨɦ ɪɚɫɫɬɨɹɧɢɢ ɞɥɹ ɧɟɤɨɪɪɢɝɢɪɨɜɚɧɧɨɣ ɩɟɪɟɞɚ-
ɱɢ, ɤɨɝɞɚ ɯ1 = 0, ɯ2 = 0 ; αtw =αt ɢ |
y = 0 . |
( .4) |
||||||||||
Ⱦɥɹ ɤɨɪɪɢɝɢɪɨɜɚɧɧɨɣ ɩɟɪɟɞɚɱɢ αtwɧɚɯɨɞɢɬɫɹ ɩɨɫɥɟ ɨɩɪɟɞɟɥɟɧɢɹ ɢɧɜɨ- |
||||||||||||
ɥɸɬɵ ɭɝɥɚ |
|
|
|
|
|
|
|
|
|
|
||
inv α |
tw |
= inv α |
t |
+ |
2(x + x2 ) |
tg α . |
( .5) |
|||||
|
||||||||||||
|
|
|
|
|
|
|
z + z2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Ɂɧɚɱɟɧɢɟ |
αtwɨɩɪɟɞɟɥɹɟɬɫɹ ɢɡ |
ɪɟɲɟɧɢɹ ɬɪɚɧɫɰɟɧɞɟɧɬɧɨɝɨ |
ɭɪɚɜɧɟɧɢɹ |
|||||||||
inv α |
tw |
= tg α |
tw |
− α |
. |
|
|
|
||||
|
|
|
|
|
|
tw |
|
|
||||
Ȼɥɨɤ-ɫɯɟɦɚ ɚɥɝɨɪɢɬɦɚ ɧɚɯɨɠɞɟɧɢɹ ɭɝɥɚ ɩɨ ɡɧɚɱɟɧɢɸ ɟɝɨ ɢɧɜɨɥɸɬɵ ɧɚ ɗȼɆ ɩɪɢɜɟɞɟɧɚ ɧɚ ɪɢɫ. . .
ɉɪɢɛɥɢɠɟɧɧɨɟ ɡɧɚɱɟɧɢɟ αtw ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɩɪɢ ɩɨɦɨɳɢ ɬɚɛɥɢɰ ɢɧɜɨ-
ɥɸɬɧɨɣ ɮɭɧɤɰɢɢ [ ].
Ⱦɥɹ ɩɪɹɦɨɡɭɛɵɯ ɤɨɥɟɫ α tw = α w
inv α |
w |
= inv α |
|
+ 2(x + x2 ) tg α . |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
z + z2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ɉɪɢ |
|
|
ɢɡɜɟɫɬɧɨɦ |
ɦɟɠɨɫɟɜɨɦ |
|
ɪɚɫɫɬɨɹɧɢɢ |
|
|
ɡɭɛɱɚɬɵɯ |
|||||||||
α tw = arccos[( |
|
d + d 2 ) cos α t |
2 aw ] . |
|
|
|
|
|
|
|||||||||
Ɇɟɠɨɫɟɜɨɟ ɪɚɫɫɬɨɹɧɢɟ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
aw = [0,5m (z + z2 ) cos α t ] (cos α tw cos |
β ) |
. |
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||||
Ʉɨɷɮɮɢɰɢɟɧɬ ɭɪɚɜɧɢɬɟɥɶɧɨɝɨ ɫɦɟɳɟɧɢɹ y [2,ɫ.75]: |
|
|
||||||||||||||||
y = x |
|
+ x |
− |
|
0,5(z |
|
+ z |
|
)[(cos α |
|
cos α |
|
)− |
|
cos |
. |
||
|
|
|
2 |
t |
tw |
] |
β |
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
Ⱦɥɹ ɤɨɥɟɫ ɛɟɡ ɫɦɟɳɟɧɢɹ x1 = x 2= 0 ; |
y = 0. |
|
|
|
|
|
|
|||||||||||
( .6)
ɤɨɥɟɫ
( .7)
( .8)
( .9)
7
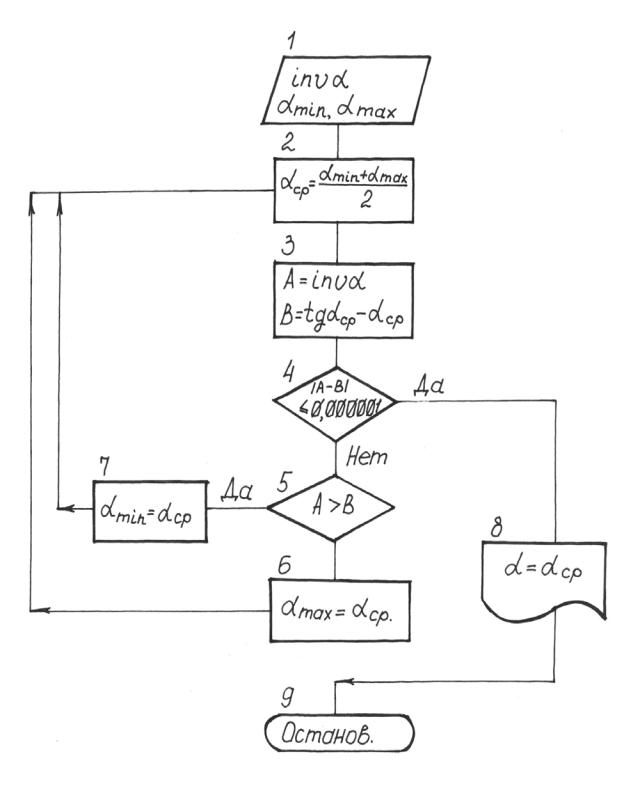
Ɋɢɫ. . . Ȼɥɨɤ-ɫɯɟɦɚ ɚɥɝɨɪɢɬɦɚ ɧɚɯɨɠɞɟɧɢɹ ɭɝɥɚ ɩɨ ɡɧɚɱɟɧɢɸ ɟɝɨ ɢɧɜɨɥɸɬɵ ɧɚ ɗȼɆ
8
ȼɵɫɨɬɚ ɝɨɥɨɜɤɢ ɡɭɛɶɟɜ ɤɨɥɟɫ
h |
a |
= (h |
* + x − |
y)m; |
h |
= (h* + x |
− |
y)m . |
( . 0) |
|
|
a |
|
a2 |
a |
2 |
|
|
|
Ⱦɢɚɦɟɬɪɵ ɜɟɪɲɢɧ ɡɭɛɶɟɜ ɤɨɥɟɫ |
|
|
|
|
|||||
d |
= d |
|
+ |
2(h* + x − y)m ; d |
|
= d |
2 |
+ 2(h* + x − |
y)m . ( . ) |
||||||
a |
|
|
|
a |
|
|
|
|
|
a2 |
a |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
||||||
ȼɵɫɨɬɚ ɡɭɛɶɟɜ ɤɨɥɟɫ |
|
|
|
|
|
|
|
|
|
|
|
||||
h = (2h* |
+ |
C * − y )m , |
|
|
|
|
|
|
|
|
|
( . 2) |
|||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɝɞɟ C* - ɤɨɷɮɮɢɰɢɟɧɬ ɪɚɞɢɚɥɶɧɨɝɨ ɡɚɡɨɪɚ (C* = 0,25). |
|
|
|||||||||||||
ȼɵɫɨɬɚ h ɦɨɠɟɬ ɛɵɬɶɩɨɞɫɱɢɬɚɧɚ ɬɚɤɠɟ ɩɨ ɮɨɪɦɭɥɟ: |
|
|
|||||||||||||
h = |
(h * |
+ h |
* )m . |
|
|
|
|
|
|
|
|
|
|
( . 3) |
|
|
a |
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
ȼɵɫɨɬɚ ɧɨɠɤɢ ɡɭɛɶɟɜ ɤɨɥɟɫ |
|
|
|
|
|
|
|
|
|
|
|||||
hf = h – ha ; hf 2 = h – ha 2 . |
|
|
|
|
|
|
|
|
|
( . 4) |
|||||
Ⱦɢɚɦɟɬɪ ɜɩɚɞɢɧ ɡɭɛɶɟɜ ɤɨɥɟɫ |
|
|
|
|
|
|
|
|
|
|
|||||
df1 = da1 -2h ; df2 = da2 -2h. |
|
|
|
|
|
|
|
|
|
( . 5) |
|||||
Ɍɨɥɳɢɧɚ ɡɭɛɚ ɧɚɪɟɡɚɟɦɨɝɨ ɢ ɫɨɩɪɹɠɟɧɧɨɝɨ ɤɨɥɟɫɚ ɧɚ ɞɟɥɢɬɟɥɶɧɨɦ ɞɢɚ- |
|||||||||||||||
ɦɟɬɪɟ (ɟɫɥɢ ɧɟ ɭɤɚɡɚɧɚ ɜ ɢɫɯɨɞɧɵɯ ɞɚɧɧɵɯ) |
|
|
|
|
|||||||||||
Sn1 |
= 0,5πm + 2 x1 m tgα - ECS1; |
|
|
|
|
|
|
||||||||
Sn2 |
= 0,5πm + 2 x2 m tgα - ECS2. |
|
|
|
|
|
( . 6) |
||||||||
ɉɪɢ ɩɪɨɟɤɬɢɪɨɜɚɧɢɢ ɲɟɜɟɪɨɜ ɪɚɫɱɟɬɧɵɟ ɡɧɚɱɟɧɢɹ Sn1 ɢ Sn2 ɨɩɪɟɞɟɥɹɸɬ- |
|||||||||||||||
ɫɹ ɫ ɭɱɟɬɨɦ ɩɨɥɨɜɢɧɵ ɜɟɥɢɱɢɧɵ ɞɨɩɭɫɤɚ ɧɚ ɬɨɥɳɢɧɭɡɭɛɚ: |
|
|
|||||||||||||
Sn1 |
= 0,5πm + 2 x1 m tgα - ECS1 |
- |
TC |
|
; |
|
|
|
|
||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
Sn2 |
= 0,5πm + 2 x2 m tgα - ECS2 |
- |
TC 2 |
|
, |
|
|
|
|
||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
ɝɞɟ ECS1 ɢ ECS2 - ɧɚɢɦɟɧɶɲɢɟ ɨɬɤɥɨɧɟɧɢɹ ɬɨɥɳɢɧɵ ɡɭɛɚ ɤɨɥɟɫɚ, ɧɟɨɛɯɨ-
ɞɢɦɵɟ ɞɥɹ ɨɛɪɚɡɨɜɚɧɢɹ ɛɨɤɨɜɨɝɨ ɡɚɡɨɪɚ ɜ ɡɭɛɱɚɬɨɦ ɡɚɰɟɩɥɟɧɢɢ. Ɂɚɜɢɫɹɬ ɨɬ ɫɬɟɩɟɧɢ ɬɨɱɧɨɫɬɢ ɤɨɥɟɫ ɢ ɜɢɞɚ ɫɨɩɪɹɠɟɧɢɹ. ȼ ɭɱɟɛɧɨɣ ɢ ɧɚɭɱɧɨ-ɬɟɯɧɢɱɟɫɤɨɣ
9
ɥɢɬɟɪɚɬɭɪɟ ɦɨɝɭɬ ɨɛɨɡɧɚɱɚɬɶɫɹ ɫɢɦɜɨɥɚɦɢ S1 ɢ S2. Ⱦɥɹ ɱɚɫɬɢ ɡɭɛɱɚɬɵɯ ɤɨ-
ɥɟɫ ɩɨ ȽɈɋɌ 643-8 [3] ɜɟɥɢɱɢɧɵ ECS ɩɪɢɜɟɞɟɧɵ ɜ ɬɚɛɥ. . .
Ɍɚɛɥɢɰɚ .
|
|
|
ɋɬɟ- |
|
Ⱦɢɚɦɟɬɪ ɞɟɥɢɬɟɥɶɧɨɣ ɨɤɪɭɠɧɨɫɬɢ, ɦɦ |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
ȼɢɞ |
|
|
|
|
ɫɜ. 80 |
ɫɜ. |
ɫɜ. |
ɫɜ. |
ɫɜ. |
ɫɜ. |
ɫɜ. |
||
ɫɨɩɪɹ- |
|
ɩɟɧɶ |
|
25 |
80 |
250 |
3 5 |
400 |
500 |
||||
|
ɬɨɱɧɨ- |
ɞɨ 80 |
|
||||||||||
|
|
|
ɞɨ |
|
|
|
|
|
|
|
|||
ɠɟɧɢɹ |
|
|
|
|
|
ɞɨ |
ɞɨ |
ɞɨ |
ɞɨ |
ɞɨ |
ɞɨ |
||
|
|
|
ɫɬɢ |
|
25 |
80 |
250 |
3 5 |
400 |
500 |
630 |
||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
0,035 |
0,04 |
0,045 |
0,055 |
0,06 |
0,06 |
0,07 |
0,08 |
|
Ⱦ |
|
|
|
7 |
0,035 |
0,045 |
0,05 |
0,06 |
0,07 |
0,07 |
0,08 |
0,09 |
|
|
|
|
|
8 |
0,04 |
0,05 |
0,06 |
0,07 |
0,07 |
0,08 |
0,09 |
0, |
|
|
|
|
|
6 |
0,055 |
0,06 |
0,07 |
0,08 |
0,09 |
0, |
0, |
0, 2 |
|
ɋ |
|
|
|
7 |
0,06 |
0,07 |
0,08 |
0,09 |
0, |
0, 2 |
0, 4 |
0, 4 |
|
|
|
|
|
8 |
0,07 |
0,08 |
0,09 |
0, |
0, 2 |
0, 4 |
0, 4 |
0, 6 |
|
|
|
|
|
6 |
0,09 |
0, |
0, 2 |
0, 4 |
0, 6 |
0, 6 |
0, 8 |
0,2 |
|
ȼ |
|
|
|
7 |
0, |
0, 2 |
0, 4 |
0, 4 |
0, 8 |
0, 8 |
0,2 |
0,22 |
|
|
|
|
|
8 |
0, |
0, 2 |
0, 4 |
0, 6 |
0, 8 |
0,2 |
0,22 |
0,25 |
|
ɇɚɢɛɨɥɶɲɢɣ ɪɚɞɢɭɫ ɤɪɢɜɢɡɧɵ ɩɪɨɮɢɥɹ ɡɭɛɚ ɧɚɪɟɡɚɟɦɨɝɨ ɤɨɥɟɫɚ |
|
|
|||||||||||
ρ |
a |
= 0,5 |
d 2 |
− d 2 |
|
|
|
|
|
|
( |
|
|
|
|
|
a |
b . |
|
|
|
|
|
|
. 7) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɋɚɞɢɭɫ ɤɪɢɜɢɡɧɵ ɜ ɬɨɱɤɟ ɧɚɱɚɥɚ ɚɤɬɢɜɧɨɣ ɱɚɫɬɢ ɩɪɨɮɢɥɹ ɡɭɛɚ ɧɚɪɟɡɚɟɦɨɝɨ ɤɨɥɟɫɚ
ρ |
a |
= a |
w |
sinα |
tw |
− 0,5 |
d 2 |
− d 2 |
( |
|
p |
|
|
|
|
a 2 |
b2 . |
. 8) |
|||
Ⱦɥɢɧɚ ɚɤɬɢɜɧɨɣ ɱɚɫɬɢ ɥɢɧɢɢ ɡɚɰɟɩɥɟɧɢɹ |
|
|
||||||||
L= 0,5( d2 |
−d2 + |
d2 |
−d2 |
)−a |
sinα . |
( . 9) |
a |
b |
a2 |
b2 |
w |
tw |
|
ɇɟɨɛɯɨɞɢɦɨɟ ɩɪɢ ɲɟɜɢɧɝɨɜɚɧɢɢ ɩɟɪɟɤɪɵɬɢɟ ɨɛɪɚɛɨɬɤɨɣ ɚɤɬɢɜɧɨɣ ɱɚɫɬɢ |
||||||
ɩɪɨɮɢɥɹ ɡɭɛɚ ɧɚɪɟɡɚɟɦɨɝɨ ɤɨɥɟɫɚ |
|
|
|
|||
L = 0, 5m sinαtw . |
|
|
|
|
( .20) |
|
ɍɝɨɥ ɧɚɤɥɨɧɚ ɜɢɧɬɨɜɨɣ ɥɢɧɢɢ ɧɚ ɨɫɧɨɜɧɨɦ ɰɢɥɢɧɞɪɟ ɤɨɥɟɫɚ ɩɨ ɨɬɧɨɲɟ-
ɧɢɸ ɤ ɬɨɪɰɭ (ɞɥɹ ɤɨɫɨɡɭɛɵɯ ɤɨɥɟɫ)
0
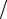
σ = arccos(cosα sinβ) . ( .2 )
Ⱦɥɹ ɩɪɹɦɨɡɭɛɵɯ ɤɨɥɟɫ σ = 90° .
Ʉɨɷɮɮɢɰɢɟɧɬ ɩɟɪɟɤɪɵɬɢɹ ɨɛɪɚɛɨɬɤɨɣ ɩɪɢ ɡɚɰɟɩɥɟɧɢɢ ɤɨɥɟɫɚ ɫ ɲɟɜɟɪɨɦ
ε = (L + L) πm (sinσ cosα ) |
( .22) |
Ⱦɨɥɠɧɨ ɛɵɬɶ ε ≥ , . ȼ ɩɪɨɬɢɜɧɨɦ ɫɥɭɱɚɟ ɲɟɜɢɧɝɨɜɚɧɢɟ ɧɟɜɨɡɦɨɠɧɨ.
ɢ ɲɟɜɟɪ ɧɟ ɩɪɨɟɤɬɢɪɭɟɬɫɹ.
ȼ ɡɚɞɚɧɢɢ ɧɚ ɤɭɪɫɨɜɨɟ ɢɥɢ ɞɢɩɥɨɦɧɨɟ ɩɪɨɟɤɬɢɪɨɜɚɧɢɟ ɜ ɤɚɱɟɫɬɜɟ ɢɫ-
ɯɨɞɧɵɯ ɞɚɧɧɵɯ ɦɨɝɭɬ ɛɵɬɶ ɭɤɚɡɚɧɵ ɧɨɦɟɪɚ ɱɟɪɬɟɠɟɣ ɡɭɛɱɚɬɵɯ ɤɨɥɟɫ, ɦɟɠ-
ɰɟɧɬɪɨɜɨɟ ɪɚɫɫɬɨɹɧɢɟ ɩɨ ɫɛɨɪɨɱɧɨɦɭ ɱɟɪɬɟɠɭ ɭɡɥɚ ɢɥɢ ɞɟɬɚɥɶɧɨɦɭ ɤɨɪɩɭɫɚ
ɭɡɥɚ, ɬɟɯɧɨɥɨɝɢɱɟɫɤɢɟ ɩɪɨɰɟɫɫɵ ɢɡɝɨɬɨɜɥɟɧɢɹ ɡɭɛɱɚɬɵɯ ɤɨɥɟɫ.
ȼ ɱɟɪɬɟɠɚɯ ɦɨɠɟɬ ɜɫɬɪɟɬɢɬɶɫɹ ɞɸɣɦɨɜɚɹ ɫɢɫɬɟɦɚ ɦɟɪ. Ɋɚɡɥɢɱɚɸɬ
ɞɢɚɦɟɬɪɚɥɶɧɵɣ ɢ ɨɤɪɭɠɧɨɣ ɩɢɬɱ. Ⱦɢɚɦɟɬɪɚɥɶɧɵɣ ɩɢɬɱ ɜɵɪɚɠɚɟɬ ɱɢɫɥɨ
ɡɭɛɶɟɜ, ɩɪɢɯɨɞɹɳɢɯɫɹ ɧɚ ɞɸɣɦ ɞɢɚɦɟɬɪɚ ɞɟɥɢɬɟɥɶɧɨɣ ɨɤɪɭɠɧɨɫɬɢ. ɉɢɬɱ ɢ
ɦɨɞɭɥɶ ɫɜɹɡɚɧɵ ɡɚɜɢɫɢɦɨɫɬɶɸ |
|
m = 25,4 / p, ɦɦ, |
( .23) |
ɝɞɟ p - ɞɢɚɦɟɬɪɚɥɶɧɵɣ ɩɢɬɱ.
Ɉɤɪɭɠɧɨɣ ɩɢɬɱ ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɲɚɝ ɦɟɠɞɭɡɭɛɶɹɦɢ ɧɚ ɞɟɥɢɬɟɥɶɧɨɣ
ɨɤɪɭɠɧɨɫɬɢ, ɜɵɪɚɠɟɧɧɵɣ ɜ ɞɸɣɦɚɯ. Ɇɟɠɞɭ ɨɤɪɭɠɧɵɦ ɩɢɬɱɟɦ P, ɞɢɚɦɟɬ-
ɪɚɥɶɧɵɦ ɩɢɬɱɟɦ p ɢ ɦɨɞɭɥɟɦ m ɫɭɳɟɫɬɜɭɟɬ ɡɚɜɢɫɢɦɨɫɬɶ:
P = π/p , ɞɸɣɦ; P = π m/25,4, ɞɸɣɦ; m = 8,09P, ɦɦ. |
( .24) |
ɏɨɪɞɚɥɶɧɵɣ ɩɢɬɱ ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɲɚɝ ɦɟɠɞɭ ɡɭɛɶɹɦɢ ɩɨ ɯɨɪɞɟ ɧɚ ɞɟɥɢɬɟɥɶɧɨɣ ɨɤɪɭɠɧɨɫɬɢ, ɜɵɪɚɠɟɧɧɨɣ ɜ ɞɸɣɦɚɯ.
ȼ ɱɟɪɬɟɠɚɯ ɦɨɠɟɬ ɜɫɬɪɟɬɢɬɶɫɹ ɢ ɞɜɭɯɦɨɞɭɥɶɧɚɹ (ɢɥɢ ɞɜɭɯɩɢɬɱɟɜɚɹ) ɫɢɫ-
ɬɟɦɚ ɡɚɰɟɩɥɟɧɢɹ, ɧɚɩɪɢɦɟɪ m1/m2. ȼ ɷɬɨɣ ɫɢɫɬɟɦɟ ɪɚɡɦɟɪɵ ɞɟɥɢɬɟɥɶɧɨɣ ɨɤ-
ɪɭɠɧɨɫɬɢ ɢ ɬɨɥɳɢɧɵ ɡɭɛɶɟɜ ɪɚɫɫɱɢɬɵɜɚɸɬɫɹ ɩɨ ɛɨɥɶɲɨɦɭ ɦɨɞɭɥɸ, ɚ ɜɵɫɨɬɵ ɡɭɛɶɟɜ - ɩɨ ɦɚɥɨɦɭ ɦɨɞɭɥɸ, ɬ.ɟ. ɤɨɥɟɫɚ ɢɦɟɸɬ ɭɤɨɪɨɱɟɧɧɭɸ ɩɪɨɬɢɜ ɨɛɵɱɧɨɣ ɜɵɫɨɬɭɡɭɛɶɟɜ.
ɇɚ ɱɟɪɬɟɠɟ ɡɭɛɱɚɬɨɝɨ ɤɨɥɟɫɚ ɦɨɠɟɬ ɛɵɬɶ ɭɤɚɡɚɧɚ ɜ ɧɨɪɦɚɥɶɧɨɦ ɫɟɱɟɧɢɢ ɤ ɧɚɩɪɚɜɥɟɧɢɸ ɡɭɛɚ ɬɨɥɳɢɧɚ ɡɭɛɚ ɩɨ ɯɨɪɞɟ Sx ɢ ɜɵɫɨɬɚ ɝɨɥɨɜɤɢ ɡɭɛɚ ɞɨ ɯɨɪ-

ɞɵ ɢ ɧɚɪɭɠɧɵɣ ɞɢɚɦɟɬɪ ɡɭɛɱɚɬɨɝɨ ɤɨɥɟɫɚ. Ɍɨɝɞɚ ɜɵɫɨɬɚ ɝɨɥɨɜɤɢ ɡɭɛɚ ha ɢ
ɬɨɥɳɢɧɚ ɡɭɛɚ ɩɨ ɞɭɝɟ ɞɟɥɢɬɟɥɶɧɨɣ ɨɤɪɭɠɧɨɫɬɢ Sn1 ɩɨɞɫɱɢɬɵɜɚɸɬɫɹ ɩɨ ɮɨɪ-
ɦɭɥɚɦ:
|
|
|
d |
|
|
|
S |
x |
|
|
h |
=h |
− |
|
|
|
|
; |
|||
|
|
|
|
|
|
|||||
|
|
|
|
|||||||
|
−cos arcsin |
d |
|
|
|
|
||||
a |
x |
|
2 |
|
|
cosβ |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sn = d cos β arcsin ( Sx /(d cos β). |
( .25) |
|||||||||
ɇɚ ɱɟɪɬɟɠɟ ɡɭɛɱɚɬɨɝɨ ɤɨɥɟɫɚ ɦɨɠɟɬ ɛɵɬɶ ɭɤɚɡɚɧ ɪɚɡɦɟɪ Ʉ ɩɨ ɪɨɥɢɤɚɦ
(ɲɚɪɢɤɚɦ) ɞɢɚɦɟɬɪɚ dɒ. Ɍɨɝɞɚ ɞɥɹ ɩɪɹɦɨɡɭɛɵɯ ɤɨɥɟɫ ɫ ɱɟɬɧɵɦ ɱɢɫɥɨɦ ɡɭɛɶ-
ɟɜ ɬɨɥɳɢɧɚ ɡɭɛɚ ɩɨ ɞɭɝɟ ɞɟɥɢɬɟɥɶɧɨɣ ɨɤɪɭɠɧɨɫɬɢ ɦɨɠɟɬ ɛɵɬɶ ɩɨɞɫɱɢɬɚɧɚ ɩɨ ɮɨɪɦɭɥɚɦ:
M = |
K − dɒ |
|
α D |
d cosα |
|
|||
; |
=arccos |
|
|
; |
||||
2M |
||||||||
2 |
||||||||
|
|
|
|
|
|
|||
Sn = d ( |
π |
+ inv αD – inv α - |
dɒ |
|
z |
d cosα |
). |
||
Ⱦɥɹ ɧɟɱɟɬɧɨɝɨ ɱɢɫɥɚ ɡɭɛɶɟɜ ɤɨɥɟɫɚ ɪɚɡɦɟɪ
K −dɒ
M = 2cos π ;
2z
ɚɜɟɥɢɱɢɧɵ αD ɢ Sn ɩɨɞɫɱɢɬɵɜɚɸɬɫɹ ɬɚɤ ɠɟ, ɩɨ ɮɨɪɦɭɥɚɦ ( .26).
( .26)
( .27)
Ⱦɥɹ ɤɨɫɨɡɭɛɵɯ ɤɨɥɟɫ ɪɚɡɦɟɪ Ɇ ɨɩɪɟɞɟɥɹɟɬɫɹ ɬɚɤ ɠɟ, ɤɚɤ ɢ ɞɥɹ ɩɪɹɦɨɡɭ-
ɛɵɯ, ɬ.ɟ. ɩɨ ɮɨɪɦɭɥɚɦ:
M = |
|
K − dɒ |
|
- ɞɥɹ ɱɟɬɧɨɝɨ ɱɢɫɥɚ ɡɭɛɶɟɜ ɤɨɥɟɫɚ ɢ |
||
2 |
|
|||||
|
|
|
|
|
||
M = |
|
K −dɒ |
|
- ɞɥɹ ɧɟɱɟɬɧɨɝɨ ɱɢɫɥɚ ɡɭɛɶɟɜ. |
||
2cos |
π |
|
||||
|
2z |
|
|
|||
|
|
|
|
|
|
|
Ɂɞɟɫɶ ɜɟɥɢɱɢɧɚ Ʉ - ɨɯɜɚɬɵɜɚɸɳɢɣ ɪɚɡɦɟɪ ɩɨ ɲɚɪɢɤɚɦ.
Ɍɨɥɳɢɧɚ ɡɭɛɚ ɩɨ ɧɨɪɦɚɥɢ ɧɚ ɞɟɥɢɬɟɥɶɧɨɣ ɨɤɪɭɠɧɨɫɬɢ ɤɨɫɨɡɭɛɨɝɨ ɤɨɥɟ-
ɫɚ ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɨ ɮɨɪɦɭɥɚɦ:
2

|
|
|
|
tgα |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
d cos arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
α D |
= |
|
cos β |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||
2M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ó = arccos[cos (arctg |
|
tgá |
)sin â] ; |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
cos â |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
tgα |
|
|
|
|
|
|
|
|
|
|
|
|
|
ɒ |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
−invα |
|
+inv arctg |
|
|
|
|
|
|||
Sn1= π |
|
m – d1cos β |
|
|
|
|
|
|
|
|
|
|
D |
|
|
. |
( |
.28) |
|||
|
|
|
|
|
|
|
|
|
tgα |
|
|
|
|
cosβ |
|
|
|
||||
|
|
|
d |
cos arctg |
sinσ |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
cosβ |
|
|
|
|
|
|
|
|
|||||
Ɋɚɫɱɟɬ ɞɨɩɨɥɧɢɬɟɥɶɧɵɯ ɬɟɯɧɨɥɨɝɢɱɟɫɤɢɯ ɩɚɪɚɦɟɬɪɨɜ ɲɥɢɰɟɜɵɯ ɜɚɥɨɜ ɫ ɷɜɨɥɶɜɟɧɬɧɵɦɢ ɡɭɛɶɹɦɢ ɧɟ ɨɬɥɢɱɚɟɬɫɹ ɨɬ ɪɚɫɱɟɬɚ ɩɚɪɚɦɟɬɪɨɜ ɡɭɛɱɚɬɵɯ ɤɨ-
ɥɟɫ. Ɉɫɨɛɟɧɧɨɫɬɶɸ ɪɚɫɱɟɬɚ ɡɭɛɨɪɟɡɧɨɝɨ ɢɧɫɬɪɭɦɟɧɬɚ (ɱɟɪɜɹɱɧɵɯ ɮɪɟɡ, ɞɨɥ-
ɛɹɤɨɜ) ɜ ɷɬɨɦ ɫɥɭɱɚɟ ɹɜɥɹɟɬɫɹ ɧɟɨɛɯɨɞɢɦɨɫɬɶ ɨɩɪɟɞɟɥɟɧɢɹ ɞɢɚɦɟɬɪɚ ɨɤɪɭɠ-
ɧɨɫɬɢ, ɫɨɨɬɜɟɬɫɬɜɭɸɳɟɣ ɧɚɱɚɥɭɪɚɛɨɱɟɣ ɱɚɫɬɢ ɩɪɨɮɢɥɹ ɡɭɛɚ ɜɚɥɚ dp .
ȿɫɥɢ ɷɬɨɬ ɞɢɚɦɟɬɪ ɧɚ ɱɟɪɬɟɠɟ ɧɟ ɭɤɚɡɚɧ, ɬɨ ɫɥɟɞɭɟɬ ɨɛɪɚɬɢɬɶɫɹ ɤ ɫɬɚɧ-
ɞɚɪɬɭɧɚ ɲɥɢɰɟɜɵɟ ɫɨɟɞɢɧɟɧɢɹ ɋɌ ɋɗȼ 268-76 [4].
Ⱥ ɪɚɞɢɭɫ ɤɪɢɜɢɡɧɵ ɜ ɬɨɱɤɟ ɧɚɱɚɥɚ ɚɤɬɢɜɧɨɣ ɱɚɫɬɢ ɩɪɨɮɢɥɹ ɡɭɛɚ ɜɚɥɚ ɪɚɫɫɱɢɬɚɬɶ ɩɨ ɮɨɪɦɭɥɟ:
ρ P = |
d |
2 |
d |
|
2 |
|
||
|
|
P |
− |
|
b |
. |
( .29) |
|
|
|
2 |
|
2 |
|
|
||
ɋ ɰɟɥɶɸ ɭɜɟɥɢɱɟɧɢɹ ɩɪɨɢɡɜɨɞɢɬɟɥɶɧɨɫɬɢ ɢ ɬɨɱɧɨɫɬɢ ɢɡɝɨɬɨɜɥɟɧɢɹ ɲɥɢɰɟɜɵɟ ɜɚɥɵ ɫ ɩɪɹɦɨɥɢɧɟɣɧɵɦ ɩɪɨɮɢɥɟɦ ɡɭɛɶɟɜ ɩɨ ȽɈɋɌ 39-80 ɢɥɢ ɫɩɟɰɢɚɥɶɧɵɟ ɨɛɪɚɛɚɬɵɜɚɸɬɫɹ ɬɚɤɠɟ ɩɨ ɦɟɬɨɞɭ ɨɛɤɚɬɚ ɫ ɩɨɦɨɳɶɸ ɱɟɪɜɹɱɧɵɯ ɮɪɟɡ ɢ ɞɨɥɛɹɤɨɜ.
ɇɚ ɪɢɫ. .2 ɩɪɟɞɫɬɚɜɥɟɧɵ ɩɨɩɟɪɟɱɧɨɟ ɫɟɱɟɧɢɟ ɲɥɢɰɟɜɨɝɨ ɜɚɥɚ ɢ ɜɚɪɢɚɧ-
ɬɵ ɟɝɨ ɢɫɩɨɥɧɟɧɢɹ ɩɨ ȽɈɋɌ 39-80 [5].
ɇɚ ɪɢɫ. .2 ɨɛɨɡɧɚɱɟɧɢɹ:
D - ɧɨɦɢɧɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɧɚɪɭɠɧɨɝɨ ɞɢɚɦɟɬɪɚ; d(d )- ɧɨɦɢɧɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɜɧɭɬɪɟɧɧɟɝɨ ɞɢɚɦɟɬɪɚ; b - ɧɨɦɢɧɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɲɢɪɢɧɵ ɡɭɛɚ.
3
