ferma / ДИПЛОМ БАКАЛАВРА / диплом 5 курс / ___Диплом Гончаров____ / _Дипломs / Дипломы теплотехников / Пояснит. Записка / По разделам / 8.4 АСР разрежения

8.4 Автоматическая система регулирования разрежения в топке котла

8.4.1 Расчет динамических характеристик элементов АСР

Структурная схема АСР разрежения приведена на рисунке 8.19, где

W_р(р)– передаточная функция регулятора разрежения;

W_об(р) – передаточная функция объекта регулирования;

W_дф(р) – передаточная функция демпфера;

W_им(р) – передаточная функция исполнительного механизма (ИМ) регулятора разрежения;

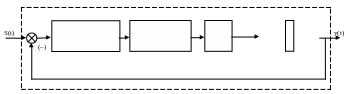
Рисунок 8.19 – Структурная схема одноконтурной АСР

На основании полученной кривой разгона при возмущении расходом газа (таблице 8.14, рисунок 8.20, 8.21).

Рисунок 8.20 – Возмущающее воздействие

Таблица 8.14 – Значение разрежения

от времени

t, c	δсг,кгс/м2	Δоп,кгс/м2
0	0	0
2	0,1	0,9
4	1,05	0,85
8	1,8	1,5
10	1,93	1,6
12	1,98	1,79
14	1,99	1,86
16	2	1,99

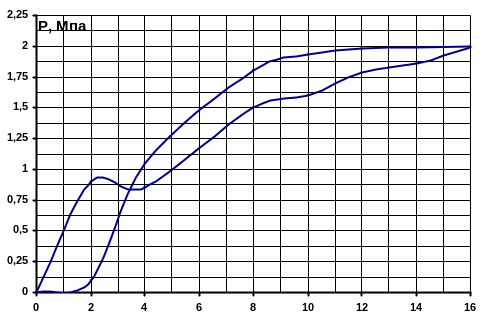
Рисунок 8.21 – Кривая разгона АСР разрежения

Полученная кривая разгона (рисунок 8.21) представляет собой S-образную временную характеристику. В таком случае для определения динамических параметров объекта воспользуемся методом Круг-Мининой [7]. Согласно этого метода по кривой разгона объекта регулирования (рисунок 8.21) графическим методом определяем с и с, при которых ординаты временной характеристики составляют кгс/м² и кгс/м² соответственно, где кгс/м².

Вычисляем динамические параметры объекта:

- время чистого запаздывания

, с (8.42)

с;

- постоянная времени объекта

, с (8.43)

с;

- коэффициент передачи объекта

(8.44)

(кгс/м²)/%.

Передаточная функция объекта регулирования будет иметь

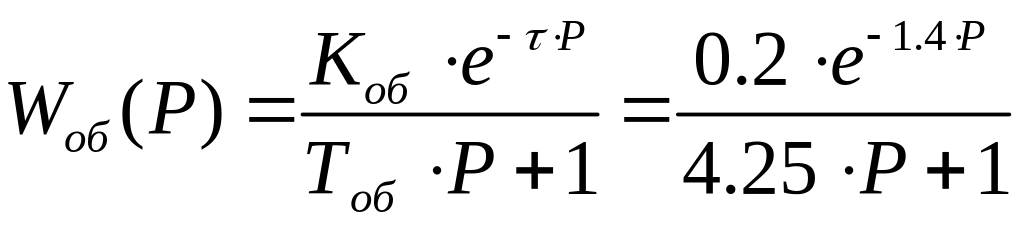, (кгс/м²)/%. (8.45)

Передаточная функция исполнительного механизма регулятора разрежения:

, (8.46)

где Т_им – постоянная времени ИМ регулятора разрежения, с;

.

Передаточная функция демпфера измерительной цепи регулятора:

, (8.47)

где Т_дф – настраиваемая величина, с;

для регулятора типа Ремиконт – 130

Т_дф = 0,04+α·1.32,

α – значение потенциометра “Демпфер” в регуляторе (изменяется от 0 до 1).

При максимальном значении α = 1 находим передаточную функцию демпфера

Передаточная функция датчика, т.к. инерционность датчика мала, считаем его усилительным звеном

, (8.48)

где К_д - номинальный статический коэффициент усиления датчика разрежения, мА/( кгс/м²):

, (8.49)

где I – выходной токовый сигнал датчика равный 4÷20 мА,

Р – перепад давления равный 2,5 кгс/м²:

мА/( кгс/м²).

Передаточная функция датчика

8.4.2 Расчет границы области заданного запаса устойчивости

При расчете границы области заданного запаса устойчивости будем использовать метод расширенных амплитудно-фазо-частотных характеристик (РАФЧХ).

Исходными для определения границы области заданного запаса устойчивости m = m_зд = 0,478 является выражение (ф.8.37).

Так, для объекта регулирования с передаточной функцией (ф.8.45) граница области заданного запаса устойчивости определяется выражениями:

Задавая различные значения ω найдем границу заданного запаса устойчивости.

По формулам (8.12) рассчитаем границу заданного запаса устойчивости для данной передаточной функции (8.8) в оболочке Mathcad 2001 Professional

(приложение Ж), численные значения сведем в таблицу 8.15. По этим численным значения в пространстве параметров настройки построим границу заданного запаса устойчивости (рисунок 8.22), по которой, используя первый интегральный критерий, определяем оптимальные параметры настройки регулятора:

– коэффициент регулятора: %/mA;

– время изодромы: с.

В таком случае передаточная функция регулятора в численном виде будет выглядеть: 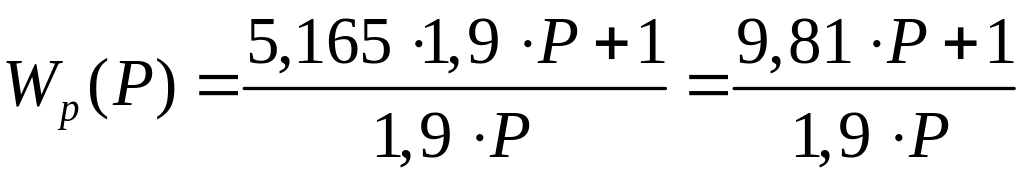, %/mA.

Таблица 8.15 – Расчетные

значения параметров настройки

Кр,%/mA	Кр/Ти,%/(mA·c)
-2.367	0
-1.646	0.132
-0.702	0.486
0.402	0.989
1.602	1.555
2.835	2.092
4.042	2.508
5.165	2.718
6.153	2.644

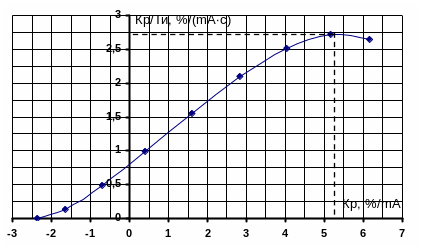Рисунок 8.22 – Граница заданного

запаса устойчивости ПИ-регулятора

8.4.3 Построение переходных процессов по каналу f и S

и определение оценок качества процессов

Полная схема, по каналу задающего воздействия f(t) y(t), которая показана на рисунке 8.19.

Передаточная функция эквивалентного объекта будет иметь вид:

, mA, (8.50)

где – передаточная функция объекта регулирования;

, – передаточные функции датчиков давления воздуха и газа перед котлом;

– передаточная функция исполнительного механизма.

Подставляя численные значения передаточных функций входящих в передаточную эквивалентного объекта и заменяя оператор на , получим

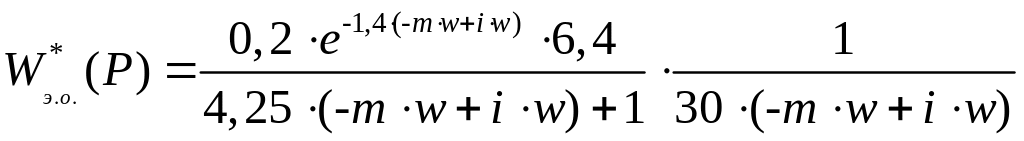, mA.

Передаточная функция эквивалентного регулятора будет иметь вид:

, (8.51)

где – передаточная функция регулятора;

– передаточная функция демпфера.

.

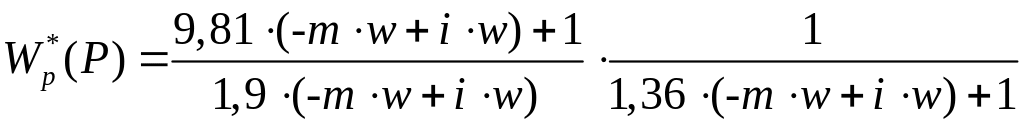Рисунок 8.23 – Структурная схема АСР топлива

W_р^*(Р) – передаточная функция регулятора;

W_об^*(Р) – передаточная функция объекта регулирования;

Переходный в замкнутой системе (рисунок 8.4.3.2) можно вычислить, используя вещественную частотную характеристику (ВЧХ). Передаточная функция такой системы будет иметь вид:

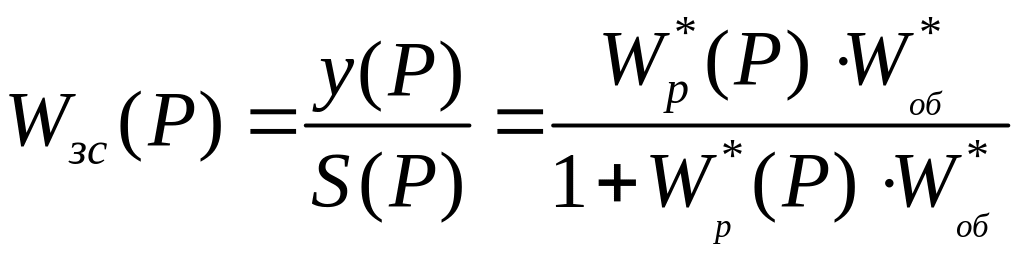. (8.52)

Заменяя оператор Р на iω, получаем АФЧХ замкнутой системы W_зс(iω).

Для приближенного построения переход­ного процесса устойчивой системы, вызванного воздейст­вием типа единичного скачка при нулевых начальных усло­виях, воспользуемся следующим интегралом ф. 8.17. Вычисление интеграла выполним в оболочке Mathcad 2001 Professional (приложение З), расчетные значения переходного процесса (рисунок 8.24) сведем в таблицу 8.16.

Таблица 8.16 – Расчетные значения переходного процесса

t, c	Y(t)
0	0
5	0,884
10	1,218
15	1,143
20	0,991
25	0,943
30	0,975
35	1,008
40	1,013
45	1,004
50	0,997
55	0,997
60	0,999
65	1
70	1
75	1

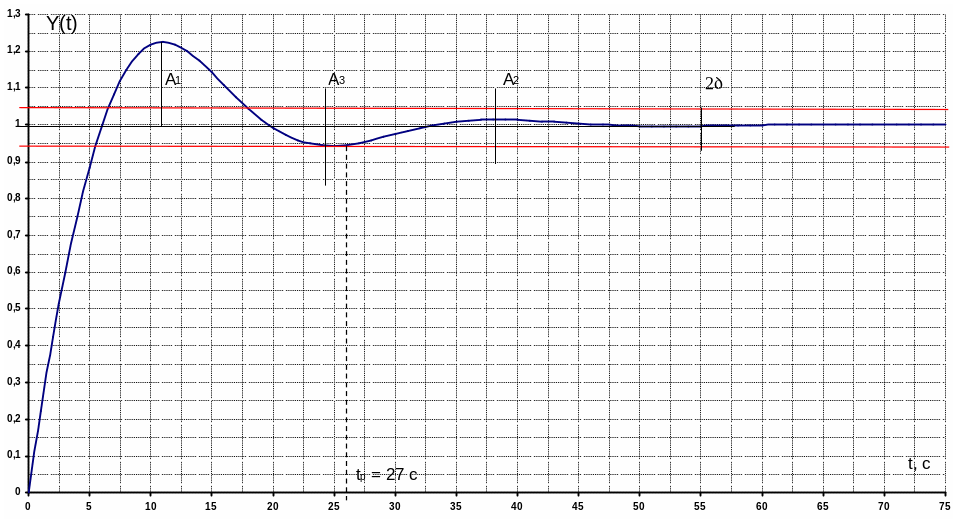
Рисунок 8.24 – Переходный процесс замкнутой системы по каналу f

По разработанной программе на кафедре АТП RAF1S “Расчет параметров настройки ПИ-регулятора в системе с объектом” ф. (8.18) и построим график переходного процесса объекта управления по каналу S.

Для этого введем исходные данные:

(кгс/см²)/%; T₀ = T₂ = T₃ = 0; Т₁ = 2,56 с; m = 0,478, а также полученные раннее ОПН регулятора.

Получаем переходный процесс по каналу возмущения, идущего со стороны регулирующего органа (рисунок 8.18).

Результаты расчета сведем в таблицу 8.13.

Т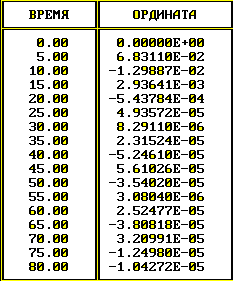 аблица 8.13 - Расчетные значения переходного процесса по каналу S

Рисунок 8.18 – Переходный процесс замкнутой системы по каналу S

Произведем прямую оценку качества полученных переходных процессов регулирования по следующим показателям:

а) длительность процесса регулирования – время, по истечении которого отклонение регулируемой величины от установившего состояния не будет превышать некоторой, наперед заданной величины

δ = 0,05 ∙ y(∞) = 0,05 ∙ 1 = 0,05,

по каналу f t_р = 27 с,

по каналу S t_р = 10 с;

б) степень затухания

по каналу f Ψ = ,

по каналу S Ψ = ;

в) величина динамической ошибки регулирования

по каналу f А₁ = 0,226,

по каналу S А₁ = 0,07;

г) величина перерегулирования

по каналу f ;

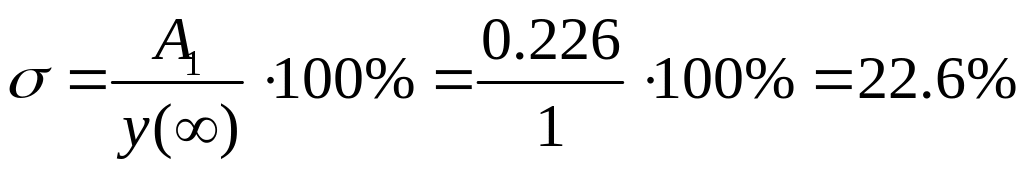по каналу S .
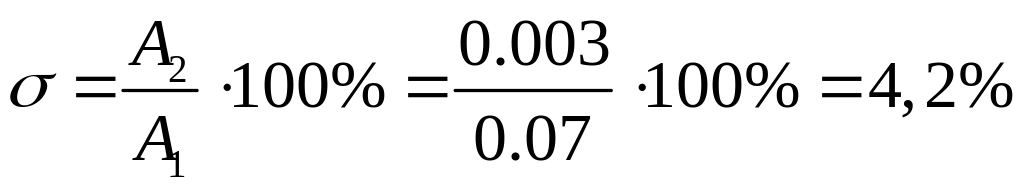