Замкнутость реляционной алгебры и операция переименования

Как мы говорили, каждое отношение характеризуется схемой (или заголовком) и набором кортежей (или телом). Поэтому, если действительно желать иметь алгебру, операции которой замкнуты относительно понятия отношения, то каждая операция должна производить отношение в полном смысле, т.е. оно должно обладать и телом, и заголовком.

Хотя в основе теоретико-множественной части реляционной алгебры лежит классическая теория множеств, соответствующие операции реляционной алгебры обладают некоторыми особенностями.

Два отношения совместимы по объединению в том и только в том случае, когда обладают одинаковыми заголовками. Более точно, это означает, что в заголовках обоих отношений содержится один и тот же набор имен атрибутов, и одноименные атрибуты определены на одном и том же домене.

Другие проблемы связаны с операцией взятия прямого произведения двух отношений. В теории множеств прямое произведение может быть получено для любых двух множеств, и элементами результирующего множества являются пары, составленные из элементов первого и второго множеств. Поскольку отношения являются множествами, то и для любых двух отношений возможно получение прямого произведения. Но результат не будет отношением! Элементами результата будут являться не кортежи, а пары кортежей.

Поэтому в реляционной алгебре используется специализированная форма операции взятия прямого произведения - расширенное прямое произведение отношений. При взятии расширенного прямого произведения двух отношений элементом результирующего отношения является кортеж, являющийся конкатенацией (или слиянием) одного кортежа первого отношения и одного кортежа второго отношения.

По поводу теоретико-множественных операций реляционной алгебры следует еще заметить, что все четыре операции являются ассоциативными. Т. е., если обозначить через OP любую из четырех операций, то (A OP B) OP C = A OP (B OP C), и следовательно, без введения двусмысленности можно писать A OP B OP C (A, B и C - отношения, обладающие свойствами, требуемыми для корректного выполнения соответствующей операции). Все операции, кроме взятия разности, являются коммутативными, т.е. A OP B = B OP A.

Ниже используются обозначения:

• A,B,C... (возможно с индексами) - имена полей (атрибуты), причем считается, что для каждого имени однозначно определен тип данных (домен) и этот тип неструктурный;

• r,s,t... (возможно с индексами) - переменные типа запись (кортеж), причем считается, что порядок полей в записи не существенен, т.е. записи с одинаковым множеством полей (и их значениями) одинаковы;

• R,S,T... (возможно с индексами) - переменные типа файл (таблица, отношение), причем считается, что порядок записей в файле не существенен и одинаковых записей в файле не может быть, т.е. файлы с одинаковым множеством записей одинаковы.

Базовый набор файлов: файлы, содержащие одну запись; базовые файлы определяются с помощью операции - (имя_поля: значение_поля, ...)

Базовый набор операций над файлами.

Теоретико-множественные:   - (объединение, пересечение и разность, соответственно). Операции применимы только к парам файлов(таблиц, отношений), имеющих одинаковую структуру (схему отношения базы данных).

Пусть R, S – отношения с эквивалентной схемой (множества кортежей с одинаковым набором атрибутов), r1...rk - кортежи отношения R и s1...sk - кортежи отношения S

• объединение () - отношение со схемой, эквивалентнойR и S, включающее все различные кортежи из R и S.

• разность - () - отношение со схемой, эквивалентнойR и S, включающее все кортежи из R, которые отсутствуют в S

• пересечение () - отношение со схемой, эквивалентнойR и S, включающее только совпадающие в R и S кортежи

• Декартово произведение ()- определено для отношений, с различными атрибутами, схема результата представляет собой конкатенацию схем отношений схем аргументов, результатом является множество всех кортежей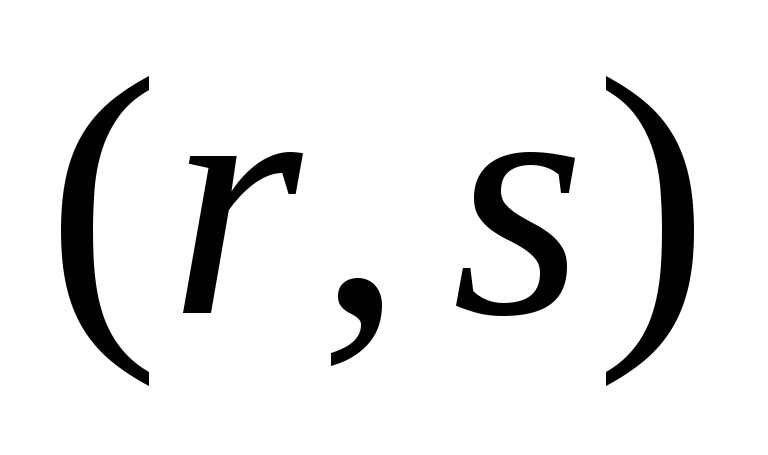, где.

• Тета-соединение. (эквивалентно. Определяет отношение, которое содержит кортежи из, удовлетворяющих предикату. Предикатможет иметь вид простого сравнения, где. Если, то говорят о соединении по эквивалентности.

• Естественное соединение (),() Естественным соединением называется соединение по эквивалентности двух отношенийи, выполненное по всем общим атрибутам, из результатов которого исключается по одному экземпляру каждого общего атрибута., где операция соединения записейиприменима только к парам записей, у которых одноименные поля имеют одинаковое значение. Соединение таких записейидает запись, в которую входят все поля (со своими значениями) изи(одноименные поля не дублируются). В случае, когда имена полей записей не пересекаются, имеем декартово произведение отношений, участвующих в операции.

ПРИМЕР.(A:1,B:2)*(B:2,C:3)=(A:1,B:2,C:3);

(A:1,B:2)*(C:3,D:4)=(A:1,B:2,C:3,D:4) - в случае файлов без одноименных полей, операция применима к каждой паре записей;

(A:1,B:2)*(B:3,D:4) - к такой паре записей операция не применима.

• Внешнее соединение. Иногда возникает ситуация, для кортежа одного отношения не находится соответствующий кортеж в другом отношении. Иначе говоря, в столбцах соединения оказываются несовпадающие значения. Если строка одного отношения должна быть представлена в результатах соединения, даже если в другом отношении нет совпадающего значения. Такое соединение называется внешним.

• Левым внешним соединением называется соединение при котором в результирующее отношение включается также кортежи отношения , не имеющие совпадающих значений в общих столбцах отношения. Для обозначения отсутствующих значений во втором отношении используются значение NULL. Аналогично определяется правое внешнее соединение. Покажите, что .

Реляционные:

• Выборка ([P](R)) () – отношение с набором кортежей из R, удовлетворяющих условию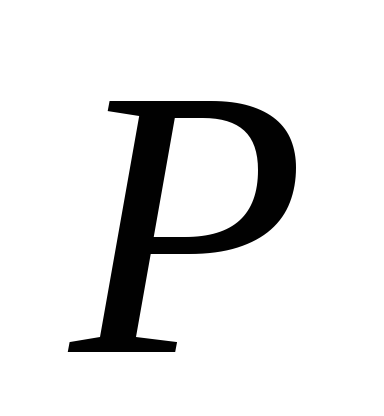. Условиестроится как обычное логическое выражение - из имен полей и констант с помощью операций сравненияи логических операций.

1. [P1 & P2](R)=[P1](R)[P2](R)

2. [P1 P2](R)=[P1](R)[P2](R)

3. [P](R)= R-[P](R)

• Проекция [имя_поля,...](R) () - файл записей из R, в которых удалены все поля, кроме перечисленных в операции. Тем самым, при выполнении операции проекции выделяется "вертикальная" вырезка отношения-операнда с естественным уничтожением потенциально возникающих кортежей-дубликатов.

• Деление RS. Операция применима, если все поля «делителя» S являются полями «делимого» R; пусть A1,A2,... - поля файла S, а A1,A2,...B1,B2,... - поля файла R. Результат деления будет файлом с полями B1,B2,... RS={t: такие, что (t*s)R для любой записи s из S}. Отметим, что в этом выражении записи t и s не имеют общих полей, поэтому операция * это просто соединение записей.

ПРИМЕР. Пусть R - файл с полями (A,B), S - файл с полем (A), T=(RS) - будет файлом с полем (B):

B

T

A

S

Дополнительные операции

• Переименование полей [A1B1,A2B2,...](R). A1,A2,... должны быть именами полей файла R, а поля B1,B2,... должны иметь соответствующий тип. Результат операции будет содержать те же записи, что и файл R, но поля A1,A2,... будут соответственно переименованы на B1,B2,... Эта операция не оказывает влияние на содержимое отношения, но изменяет его схему.

• Расширение

Добавление атрибута, вычисляемого с помощью <выражения>, под именем <имя>. Помимо арифметических операций и операций сравнения могут быть использованы также итоговые функции (к списку скалярных значений):

COUNT() – количество

SUM() – сумма

AVG() – среднее

MAX() - максимальное

MIN() – минимальное

в) подведение итогов

SUMMARIZE <отношение> BY <список атрибутов> ADD <выражение1> AS <имя1>, ... , <выражение1> AS <имя1>

Групповые вычисления. Выполняется расчет значения и добавление нового атрибута под именем <имя>, но предварительно выполняется проецирование на атрибуты, указанные в <список атрибутов>. При проецировании множество кортежей исходного отношения разобьется на группы одинаковых строк отношения – проекции. Для каждой такой группы и выполняется расчет <выражение>. Так как <выражение> применяется к группе, оно должно быть обязательно итоговой функцией от атрибута или скалярного выражения, применяемой уже не к списку скалярных значений, а к столбцу значений в одной такой группе

Рассмотрим примеры: В качестве операндов в рассмотренных ниже примерах используются следующие отношения:

P(D1, D2, D3)			Q(D4,D5)		R(M, P, Q, T)				S(A, B)
1	11	x	x	1	x	101	5	a	5	a
2	11	y	x	2	y	105	3	a	10	b
3	11	z	y	1	z	500	9	a	15	c
4	12	x			w	50	1	b	2	d
					w	10	2	b	6	a
					w	300	4	b	1	b

Взятие проекции:

R(M, T)
x	a
y	a
z	a
w	b
w	b
w	b

Объединение отношений:

Пересечение отношений:

Разность отношений:

Декартово произведение:

Деление:

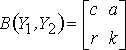
Естественное соединение:

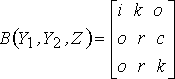
q-соединение:

Эта операция предназначается для тех случаев, когда нам нужно соединить вместе два отношения на основе некоторых условий. Пусть отношения А и В не имеют общих имен атрибутов и q определяется так же, как и в операции выборки. Тогда q-соединением отношения А по атрибуту Х с отношением В по атрибуту Y (A join B on X q Y) называется отношение с тем же заголовком, что и при декартовом произведении отношений А и В, и с телом, содержащим множество кортежей t, таких что t принадлежит этому декартову произведению и вычисление условия "X q Y" дает значение истина для этого кортежа. Атрибуты X и Y должны быть определены на одном и том же домене, а операция должна иметь смысл для этого домена.

Если q обозначает "равно", то q-соединение называется эквисоединением. Из определения следует, что результат эквисоединения должен включать два таких атрибута, значения которых должны быть равны в каждом кортеже отношения. Если один из этих атрибутов исключается (что может быть сделано операцией проекции), результатом будет просто естественное соединение.

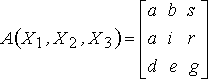
Операции изменения тела отношения

а) присвоение

<выражение-цель> := <выражение-источник>

Замена в отношении <выражение-цель> всех кортежей на кортежи отношения <выражение-источник>. При этом их схемы должны быть эквивалентны.

Обычно применяют в качестве <выражение-цель> имя отношения, а в качестве <выражение-источник> - выражение реляционной алгебры.

б) вставка INSERT <выражение-источник> INTO <выражение-цель> Добавление кортежей <выражение-источник> в отношение <выражение-цель>. Схемы отношений также должны быть эквивалентны.

в) обновление

UPDATE <выражение-цель> <список элементов>

Изменение значений атрибутов в отношении <выражение-цель> в соответствии со <список элементов>, который представляет собой последовательность вида <атрибут>:=<скалярное выражение>,…, <атрибут>:=<скалярное выражение>

г) удаление

DELETE <выражение-ограничение> FROM <выражение-цель>

Удаление в отношении <выражение-цель> кортежей, перечисленных в <выражение-ограничение>.