Сортировочный лесотранспортер.doc / 2-яя часть / Расчеты параметров рычажных бревносбрасывателей

Расчеты параметров рычажных бревносбрасывателей

Для полной сброски бревна с траверс необходимо, чтобы центр его тяжести переместился за ребро седлообразной опоры на расстояние, обеспечивающее сваливание под действием собственного веса бревна

(рис. 2. 8, а). В соответствии с этим необходимую величину хода сбрасывающих рычагов определяют по формуле

,

где - ход сбрасывающих рычагов, под которым понимается расстояние, измеренное по прямой, лежащей в горизонтальной плоскости и перпендикулярной оси транспортера, между крайними положениями конца рычага ( в исходном положении и в конце рабочего хода);

- соответственно наибольший и наименьший диаметы бревна, м;

;

- ширина опоры, м, м;

с – расстояние между рычагом, находящимся в исходном положении, и бревном максимального диаметра, м, м ;

- поперечное смещение тягового устройства под влиянием усилия сброски ( мм);

- величина на которую должен сместиться центр тяжести бревна за ребро опоры, м, , м,

м.

На величину усилия сброски оказывают влияние размеры и вес бревна, характер его движения в поперечном направлении по опоре (скольжение, качение), скорость сброски и конструкция сбрасывателя.

Рис. 2. 8 Схемы к расчетам рычажных бревносбрасывателей

На рис. 2. 8, б изображена схема расположения сил, действующих на бревно в начальный период сброски, для случая скольжения бревна по седлообразной опоре с углом подъема α. На бревно действуют следующие: усилие сброски P; вес бревна Q; реакция опоры N; силы трения и :

, ,

где , - соответственно коэффициенты трения скольжения между рычагом сбрасывателя и бревном и между бревном и опорой, , ;

сила инерции массы бревна , возникающая вследствие того, что бревно в начальный период сброски движется с ускорением;

,

где - ускорение свободного падения;

- ускорение движения бревна в поперечном направлении.

Усилие Р направлено под углом β к горизонту. Примем для расчетов, что β > α, то бревно при его поперечном перемещении опускается относительно рычагов сбрасывателя и сила трения направлена вверх. Принимаем α = 25⁰, β= 30⁰.Проектируя на оси x и у все силы, действующие на бревно, для случая

β > α ( ось x параллельна ребру опоры) получим:

;

.

Решая эти уравнения относительно P, находим

.

Определим максимальный вес бревна

,

где - плотность древесины, кг/м³;

l- длина бревна, м.

Н.

Для расчетов принимаем усилие, необходимое для сброски бревен

P=15 кН.

Общий момент, передаваемый валом на сбрасыватели

,

где - плечо сбрасывателя, м;

кН.

Момент на одном сбрасывателе

,

где n – количество сбрасывателей;

кН.

Результирующий момент на среднем сбрасывателе

;

кН.

Усилие, прикладываемое одним сбрасывателем к бревну

;

кН.

Сила трения одного сбрасывателя о бревно

,

где - коэффициент трения сбрасывателей о бревно, .

кН.

Усилие, необходимое на штоке гидроцилиндра

,

где - плечо, на котором приложено усилие гидроцилиндра к валу, м;

кН.

Результирующие силы приложенные к валу

;

кН.

;

где - равнодействующая в вертикальной плоскости,

;

кН;

кН.

Расчет вала

Рис. 2.9 Схема для расчета вала

Построим схему результирующих сил, действующих в одной плоскости

(рис. 2.10).

1. Для данной системы сил определим степень статической неопределимости

,

где - количество опорных связей данной системы;

3 - количество уравнений равновесия статики, которое может быть составлено для данной системы.

.

Система один раз статически неопределима.

2. Выбираем основную систему, отбрасываем одну реакцию

опоры (рис. 2. 10).

3. Записываем для данной системы уравнение деформации

,

где - единичный коэффициент при неизвестной силе;

- единичная сила;

- грузовой коэффициент.

4. а)Строим эпюры от изгибающих моментов от действия единичных сил и заданной нагрузки (рис. 2. 10).

б) Определим единичный коэффициент канонического уравнения.

,

где - площадь элементарной фигуры;

- ордината эпюры, взятая под центром тяжести элементарной фигуры.

;

; ;

; ;

.

в) Определим грузовой коэффициент канонического уравнения.

;

;

; ; ; ; ; .

; ; ; ; ; .

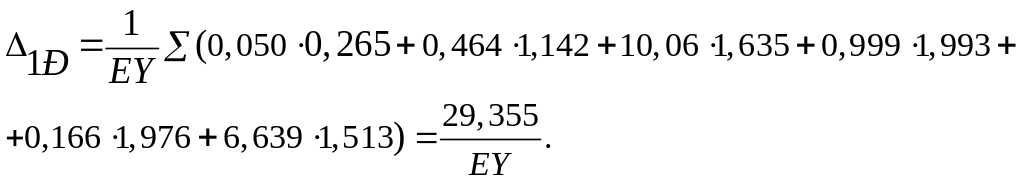
5. Определяем внешнюю неизвестную

;

кН;

кН.

Рис. 2. 10 Расчетные схемы

6. Определим опорные реакции

;

: ;

;

кН;

;

кН.

7. Строим эпюру изгибающих моментов (рис. 2. 11)

;

;

кНм;

кНм;

;

кНм;

кНм;

; кНм; ;

кНм;

; кНм;

кНм.

8. Строим эпюру крутящих моментов (рис. 2. 11)

;

кНм;

;

кНм;

кНм;

9. Строим эпюру суммарных моментов (рис. 2. 11)

;

кНм;

кНм;

кНм;

кНм;

кНм;

кНм;

кНм;

кНм.

Рис. 2. 11 Расчетные схемы