Пояснит. Записка / По разделам / 8.3 АСР воздуха

8.3 АСР воздуха

8.3.1 Динамические характеристики элементов АСР воздуха

Структурная схема АСР топлива приведена на рисунке 8.12, где приняты следующие обозначения:

W_р(Р)–передаточная функция регулятора,

W_об(Р)–передаточная функция объекта регулирования,

W_Рв(Р)–передаточная функция датчика давления воздуха,

W_Рг(Р)–передаточная функция датчика давления газа,

S(t)– управляющее воздействие,

y(t)–выходная характеристика,

f– задающее воздействие.

Рисунок 8.12–Структурная схема одноконтурной АСР

На основании полученной кривой разгона при возмущении расходом газа (таблице 8.10, рисунок 8.13 и 8.14).

Рисунок 8.13 – Возмущающее воздействие

Таблица 8.10 – Значение давления воздуха

перед горелками от времени

t, c	Рвсг,кгс/м2	Рвоп,кгс/м2
0	0	0,5
2	5	7,5
4	45	30,8
6	75	85
8	90	91
10	94	95
14	94	86

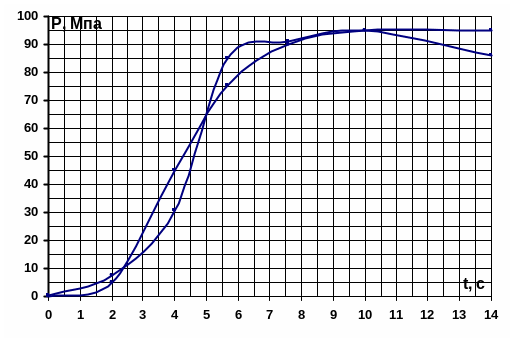
Рисунок 8.14 – Кривая разгона АСР воздуха

Полученная сглаженная кривая разгона (рисунок 8.14) представляет собой S-образную временную характеристику. В таком случае для определения динамических параметров объекта воспользуемся методом Круг-Мининой [7]. Согласно этого метода по кривой разгона объекта регулирования (рисунок 8.3.1.3) графическим методом определяем с и с, при которых ординаты временной характеристики составляют кгс/м² и кгс/м² соответственно, где кгс/м².

Вычисляем динамические параметры объекта:

- время чистого запаздывания

, с (8.29)

с;

- постоянная времени объекта

, с (8.30)

с;

- коэффициент передачи объекта

(8.31)

(кПа)/%.

Передаточная функция объекта регулирования будет иметь

, (кПа)/%. (8.32)

Рассчитаем передаточную функцию датчика давления воздуха и газа перед котлом W_Рв(P) и W_Рг(P). При применении измерительного преобразователя Метран-100-ДИ, коэффициент передачи датчиков K_Рв и K_Рг найдется как отношение выходного токового сигнала (4-20 мА) к величине перепада давления. Поскольку инерционность датчика мала, считаем его усилительным звеном , (8.33)

, (8.34)

Передаточная функция исполнительного механизма регулятора разрежения:

, (8.35)

где Т_им, с – постоянная времени ИМ регулятора воздуха, определяется его типом.

.

Передаточная функция демпфера измерительной цепи регулятора:

, (8.36)

где Т_дф – настраиваемая величина, с;

для регулятора типа Ремиконт – 130: Т_дф = 0,04+α · 1.32,

где α – значение потенциометра “Демпфер” в регуляторе (изменяется от 0 до 1).

При максимальном значении α = 1 находим передаточную функцию демпфера

8.3.2 Расчет границы области заданного запаса устойчивости

При расчете границы области заданного запаса устойчивости будем использовать метод расширенных амплитудно-фазо-частотных характеристик (РАФЧХ). Для ПИ-регулятора с передаточной функцией ф. 8.25.

Исходными для определения границы области заданного запаса устойчивости m = m_зд = 0,221 является выражение

W_p(m, iω)· W_об(m, iω)+1= 0, (8.37)

откуда W_p(m, iω) = - W_об(m, iω). (8.38)

Так, для объекта регулирования с передаточной функцией (ф. 8.32) граница области заданного запаса устойчивости определяется выражениями

(ф.8.12).

Задавая различные значения ω найдем границу заданного запаса устойчивости.

Требования к качеству переходного процесса:

– степень затухания , m = 0,478;

– первый интегральный критерий (ф. 8.13), т.к. колебательный процесс.

По формулам (ф. 8.12) рассчитаем границу заданного запаса устойчивости для данной передаточной функции (ф. 8.8) в оболочке Mathcad 2001 Professional (приложение Д), численные значения сведем в таблицу 8.11. По этим численным значения в пространстве параметров настройки построим границу заданного запаса устойчивости (рисунок 8.15), по которой, используя первый интегральный критерий, определяем оптимальные параметры настройки регулятора:

– коэффициент регулятора: %/mA;

– время изодромы: с.

В таком случае передаточная функция регулятора в численном виде будет выглядеть: , %/mA.

Таблица 8.11 – Расчетные значения

параметров настройки

Кр,%/mA	Кр/Ти,%/(mA·c)
-0,059	0
-0,052	7,42E-04
-0,042	2,81E-03
-0,031	5,90E-03
-0,019	9,70E-03
-5,98E-03	1,40E-02
7,13E-03	1,80E-02
0,02	0,022
0,032	0,024
0,044	0,026
0,054	0,027
0,063	0,025
0,07	0,022

Рисунок 8.15 – Граница заданного

запаса устойчивости ПИ-регулятора

8.3.3 Построение переходных процессов по каналу f и S

и оценка их качества

Полная схема, по каналу задающего воздействия S(t) y(t), которого показана на рисунке 8.12.

Передаточная функция эквивалентного объекта будет иметь вид:

, mA, (8.39)

где – передаточная функция объекта регулирования;

, – передаточные функции датчиков давления воздуха и газа перед котлом;

– передаточная функция исполнительного механизма.

Подставляя численные значения передаточных функций входящих в передаточную эквивалентного объекта и заменяя оператор на , получим

, mA.

Передаточная функция эквивалентного регулятора будет иметь вид:

, (8.40)

где – передаточная функция регулятора;

– передаточная функция демпфера.

.

Рисунок 8.16 – Структурная схема АСР воздуха

W_р^*(Р) – передаточная функция эквивалентного регулятора;

W_об^*(Р) – передаточная функция эквивалентного объекта регулирования;

Переходный в замкнутой системе (рисунок 8.17) можно вычислить, используя вещественную частотную характеристику (ВЧХ). Передаточная функция такой системы будет иметь вид:

. (8.41)

Заменяя оператор Р на iω, получаем АФЧХ замкнутой системы W_зс(iω).

Для приближенного построения переход­ного процесса устойчивой системы, вызванного воздейст­вием типа единичного скачка при нулевых начальных усло­виях, воспользуемся следующим интегралом ф. 8.17. Вычисление интеграла выполним в оболочке Mathcad 2001 Professional (приложение Е), расчетные значения переходного процесса (рисунок 8.17) сведем в таблицу 8.12.

Таблица 8.12 – Расчетные значения переходного процесса

t, c	Y(t)
0	0
5	1,17
10	1,249
15	0,99
20	0,929
25	0,997
30	1,022
35	1,004
40	0,994
45	0,998
50	1,002
55	1,001
60	0,999
65	1
70	1

8 .17 – Переходный процесс замкнутой системы по каналу f

По разработанной программе на кафедре АТП RAF1S “Расчет параметров настройки ПИ-регулятора в системе с объектом” ф. (8.18) и построим график переходного процесса объекта управления по каналу S.

Для этого введем исходные данные:

(кгс/см²)/%; T₀ = T₂ = T₃ = 0; Т₁ = 2,56 с; m = 0,478, а также полученные раннее ОПН регулятора.

Получаем переходный процесс по каналу возмущения, идущего со стороны регулирующего органа (рисунок 8.18).

Результаты расчета сведем в таблицу 8.13.

Таблица 8.13 - Расчетные значения переходного процесса по каналу S

Рисунок 8.18 – Переходный процесс замкнутой системы по каналу S

Произведем прямую оценку качества полученных переходных процессов регулирования по следующим показателям:

а) длительность процесса регулирования – время, по истечении которого отклонение регулируемой величины от установившего состояния не будет превышать некоторой, наперед заданной величины

δ = 0,05 ∙ y(∞) = 0,05 ∙ 1 = 0,05,

по каналу f t_р = 22 с,

по каналу S t_р = 12 с;

б) степень затухания

по каналу f Ψ = ,

по каналу S Ψ = ;

в) величина динамической ошибки регулирования

по каналу f А₁ = 0,306,

по каналу S А₁ = 0,06;

г) величина перерегулирования

по каналу f ;

по каналу S .