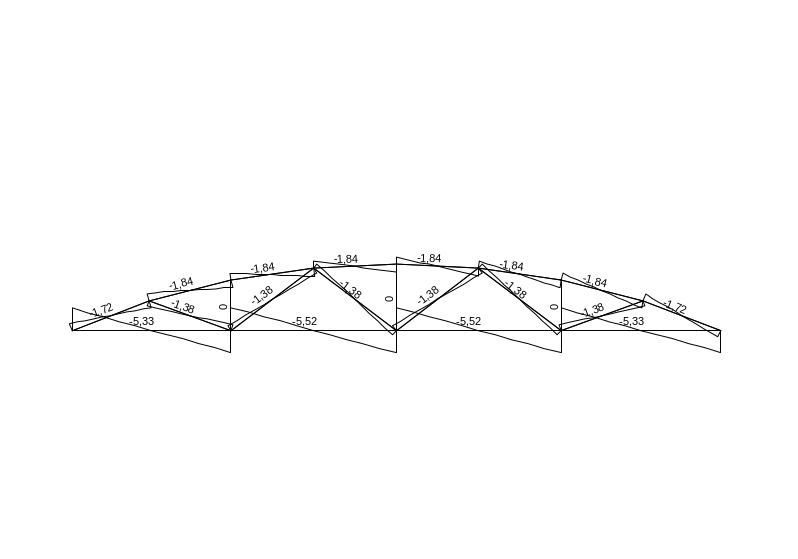
Расчетные сочетания усилий
Загружения |
|
Номер |
Наименование |
1 |
Сдвигающие силы |
2 |
Собственный вес |
Расчетные сочетания усилий, kН, м |
|||||||||||
Номер эл-та |
УНГ |
Номер сечен. |
КРТ |
CT |
КС |
Тип |
Усилия и напряжения |
Номера загружений |
|||
|
|
|
|
|
|
|
N |
M |
Q |
|
|
1 |
|
1 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-349,812 |
-,000005 |
1,71331 |
1 2 |
|
1 |
|
2 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-349,154 |
1,28709 |
-,001716 |
1 2 |
|
1 |
|
3 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-348,496 |
0, |
-1,71675 |
1 2 |
|
2 |
|
1 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-144,317 |
-,000005 |
1,83569 |
1 2 |
|
2 |
|
2 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-143,861 |
1,42131 |
-,001839 |
1 2 |
|
2 |
|
3 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-143,406 |
0, |
-1,83937 |
1 2 |
|
3 |
|
1 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-15,5534 |
-,000005 |
1,83569 |
1 2 |
|
3 |
|
2 |
1 |
1 |
|
A |
-15,2858 |
1,39408 |
-,001839 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
3 |
|
3 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-15,0181 |
0, |
-1,83937 |
1 2 |
|
4 |
|
1 |
1 |
1 |
|
A |
3,51915 |
-,000005 |
1,83569 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
4 |
|
2 |
1 |
1 |
|
A |
3,60797 |
1,38113 |
-,001839 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
4 |
|
3 |
1 |
1 |
|
A |
3,69677 |
0, |
-1,83937 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
5 |
|
1 |
1 |
1 |
|
A |
3,6966 |
-,000005 |
1,83569 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
5 |
|
2 |
1 |
1 |
|
A |
3,60778 |
1,38113 |
-,001839 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
5 |
|
3 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-52,821 |
0, |
-1,83937 |
1 2 |
|
6 |
|
1 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-15,0186 |
-,000005 |
1,83569 |
1 2 |
|
6 |
|
2 |
1 |
1 |
|
A |
-15,2863 |
1,39408 |
-,001839 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
6 |
|
3 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-141,374 |
0, |
-1,83937 |
1 2 |
|
7 |
|
1 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-143,407 |
-,000005 |
1,83569 |
1 2 |
|
7 |
|
2 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-143,862 |
1,42131 |
-,001839 |
1 2 |
|
7 |
|
3 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-402,628 |
0, |
-1,83937 |
1 2 |
|
9 |
|
1 |
1 |
1 |
|
A |
67,8576 |
-,000004 |
1,37677 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
9 |
|
2 |
1 |
1 |
|
A |
68,351 |
1,09895 |
-,001379 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
9 |
|
3 |
1 |
1 |
|
A |
68,8443 |
0, |
-1,37953 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
10 |
|
1 |
1 |
1 |
|
A |
8,86485 |
0, |
0, |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
10 |
|
2 |
1 |
1 |
|
A |
9,70001 |
0, |
0, |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
10 |
|
3 |
1 |
1 |
|
A |
10,5351 |
0, |
0, |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
11 |
|
1 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-30,7551 |
-,000005 |
1,37677 |
1 2 |
|
11 |
|
2 |
1 |
1 |
|
A |
-29,7192 |
1,29434 |
-,001379 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
11 |
|
3 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-28,6832 |
0, |
-1,37953 |
1 2 |
|
12 |
|
1 |
1 |
1 |
|
A |
18,2824 |
-,000005 |
1,37677 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
12 |
|
2 |
1 |
1 |
|
A |
17,2465 |
1,29434 |
-,001379 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
12 |
|
3 |
1 |
1 |
|
A |
16,2106 |
0, |
-1,37953 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
13 |
|
1 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-6,23644 |
0, |
0, |
1 2 |
|
13 |
|
2 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-5,13392 |
0, |
0, |
1 2 |
|
13 |
|
3 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-4,03139 |
0, |
0, |
1 2 |
|
14 |
|
1 |
1 |
1 |
|
A |
16,2127 |
-,000005 |
1,37677 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
14 |
|
2 |
1 |
1 |
|
A |
17,2486 |
1,29434 |
-,001379 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
14 |
|
3 |
1 |
1 |
|
A |
18,2845 |
0, |
-1,37953 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
15 |
|
1 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-28,6853 |
-,000005 |
1,37677 |
1 2 |
|
15 |
|
2 |
1 |
1 |
|
A |
-29,7212 |
1,29434 |
-,001379 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
15 |
|
3 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-30,7571 |
0, |
-1,37953 |
1 2 |
|
16 |
|
1 |
1 |
1 |
|
A |
8,86485 |
0, |
0, |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
16 |
|
2 |
1 |
1 |
|
A |
9,70001 |
0, |
0, |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
16 |
|
3 |
1 |
1 |
|
A |
10,5351 |
0, |
0, |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
17 |
|
1 |
1 |
1 |
|
A |
67,8576 |
-,000004 |
1,37677 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
17 |
|
2 |
1 |
1 |
|
A |
68,351 |
1,09895 |
-,001379 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
17 |
|
3 |
1 |
1 |
|
A |
68,8443 |
0, |
-1,37953 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
23 |
|
1 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-348,498 |
-,000005 |
1,71331 |
1 2 |
|
23 |
|
2 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-349,155 |
1,28709 |
-,001716 |
1 2 |
|
23 |
|
3 |
1 |
4 |
|
A |
|
|
|
|
|
|
|
|
2 |
1 |
|
A |
-694,893 |
0, |
-1,71675 |
1 2 |
|
24 |
|
1 |
1 |
1 |
|
A |
648,187 |
-,00003 |
5,32352 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
24 |
|
2 |
1 |
1 |
|
A |
648,187 |
7,73455 |
-,005334 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
24 |
|
3 |
1 |
1 |
|
A |
648,187 |
0, |
-5,33418 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
25 |
|
1 |
1 |
1 |
|
A |
736,296 |
-,000033 |
5,50709 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
25 |
|
2 |
1 |
1 |
|
A |
736,296 |
8,27717 |
-,005518 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
25 |
|
3 |
1 |
1 |
|
A |
736,296 |
0, |
-5,51812 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
26 |
|
1 |
1 |
1 |
|
A |
736,296 |
-,000033 |
5,50709 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
26 |
|
2 |
1 |
1 |
|
A |
736,296 |
8,27717 |
-,005518 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
26 |
|
3 |
1 |
1 |
|
A |
736,296 |
0, |
-5,51812 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
27 |
|
1 |
1 |
1 |
|
A |
648,187 |
-,00003 |
5,32352 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
27 |
|
2 |
1 |
1 |
|
A |
648,187 |
7,73455 |
-,005334 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
27 |
|
3 |
1 |
1 |
|
A |
648,187 |
0, |
-5,33418 |
1 2 |
|
|
|
|
2 |
4 |
|
A |
|
|
|
|
|
