ITIS0

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2 sin cos sin

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

3.31 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 166 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Анализируя

1
n 1		2n 1
2n 1	x	2n 1
	x
	!

первые члены разложения, записываем его общий член

. В результате

sin x

1 n 1

x2n 1

rn x .

2n 1

1! 3!

Оценим

rn (x)

| rn (x) | | x |2n 1 , так как

(2n 1)!

| sin(x

(2n

1)		)
	2

| 1

Пример f x cos

3. Получим разложение по формуле Маклорена функции x.


f x sin x ,				f x cos x ,				f x sin x ,	f
f	V	x sin x ,		f	VI	x cos x .

Очевидно, что
f	0 1,		f 0 0 ,			f 0 1,		f 0 0 ,
f IV 0 1,			f V 0 0 ,				f VI 0 1.

В соответствии с формулой Маклорена получаем

cos x 1

1 n

x2n rn x

2n !

x cos x

Оценим

rn(x)

	2(n 1)
\| r (x)\|	\| x\|
n	(2n 2)!
	(2n 2)!

, так как

| cos(x

(2n

2)) 2

Пример

Получим

разложение по формуле

Маклорена

функции

f x ln(1 x).

Поскольку

f (n) (x) ( 1)n 1(n 1)!,

(0! 1) ,

имеем

(1 x)n

(n)

(0)

( 1)

n 1

1)!,

поэтому получим разложение

( 1)

n 1

ln(1 x) x

...

r (x).

Оценим

rn(x).

Согласно

приведенной формуле

остаточного члена

имеем | rn(x)|

| x|(n 1)

Поэтому для x 0 получим оценку

(n 1) |1 x |(n 1)

(n 1)

| rn(x)|

| x|

но

для x 0

использование

приведенной

формулы

(n 1)

остаточного члена не годится.

Для таких значений

используют другие

формы остаточного члена.

Пример

Получим

разложение по формуле Маклорена функции

x (1 x) ,

N .

Дифференцируя, найдем

	(n)	n	,

(1 x)		( 1)( 2)...( n 1)(1 x)

поэтому

f	(n)	(0)	( 1)( 2)...( n 1),

и имеем разложение

(1 x)

1 x	( 1)	x	2	...	(
1 x		x		...

	2!

1)(

2)...( n!

n 1)

x	n

rn (x)

Для оценки остаточного члена при

, больших или равных целой части

приведенная форма остаточного этом случае оценка следующая: |

члена годится также только для

r (x)\|	\| ( 1)( 2)...( n) \|	\| x

n	(n 1)!

x |(n1)

. В

Пример применения локальной формулы Маклорена для вычисления предела

											1		x	2	x	4	o(x	4	)	(1	x	2	x	4	o(x	4
	cos x e					x2	/ 2						x		x			4			x		x			4	))
						x2	/ 2						2		24						2		8				))
lim									lim
lim				4					lim											4
x0			x	4						x0									x	4
x0			x							x0									x
		x	4	o(x				4
		x						4	)		1
		12							)
lim												.
lim				x	4						12	.
x0				x							12

Приложения производной функции

Правило Лопиталя

(Правило раскрытия неопределенностей

f x

Пусть требуется

вычислить предел

lim

причем

функции в

g x

x a

числителе и знаменателе

дифференцируемы в окрестности точки a и имеет

место одна из неопределенностей

или

, тогда если существует предел

lim

, возможно, равный бесконечности, то

lim

g x

x a

g x

Доказательство (для

неопределенности

Поскольку f a g a 0 ,

(иначе не будет указанной неопределенности), из теоремы Коши имеем

f x

f x f a

lim

g x

g x g a

x a

c a

x a

g c

g x

Здесь

x a

использовалось, что

и c a .

находится между

, следовательно, при

Примеры.

		x	2	3x 2			0
1)	lim							lim
					2	4
	x 2			x			0	x 2

	2x 3
	2x
	2x

1 4

Раньше это пример решался с помощью тождественного преобразования

lim	x2	3x 2	lim	x 2 x 1	lim	x 1	1	.
		x2 4		x 2 x 2		x 2	4
x 2			x 2		x 2

		sin x	0		cos x
2)	lim	sin x	0	lim	cos x	1
2)	lim	x	0	lim	1	1
	x 0	x	0	x 0	1

(доказан первый замечательный предел).

Теорема о возрастании (убывании) функции интервале

y f x

на

Необходимое условие возрастания (убывания)

функции на интервале: Если

функция

y f x ,

имеющая производную на интервале

(a,b) , возрастает

(убывает) на этом интервале, то ее производная

f x 0

( f x 0 ) на этом

отрезке.

Доказательство

следует

из формулы для

производной

f (x

)

f (x x) f (x

)

lim

, где

знаки

числителя

знаменателя

x 0

совпадают (противоположны), а при предельном переходе знак неравенства становится нестрогим.

Достаточное условие возрастания

функция y f x непрерывна на интервале (a, b) , причем f x 0

(убывания) функции на интервале: Если

отрезке [a, b]	и дифференцируема на
( f x 0 ) для	a x b , то эта функция

возрастает (убывает) на этом отрезке.

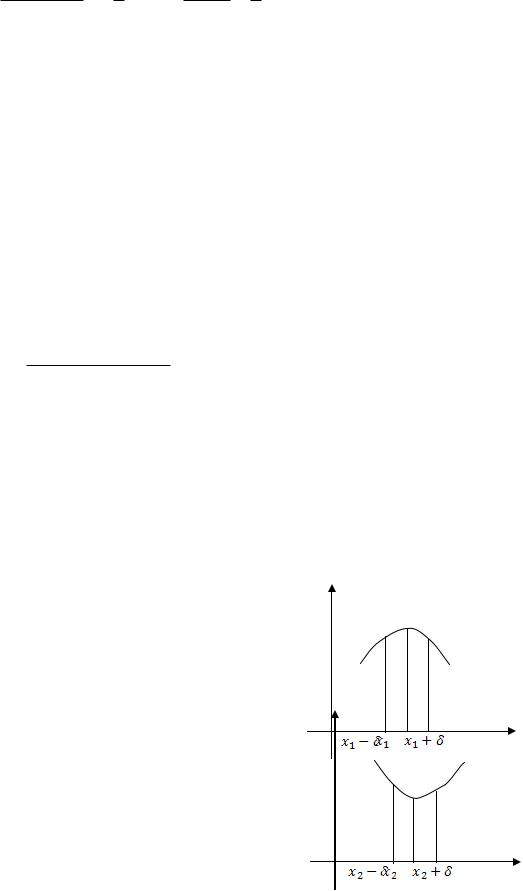
Доказательство легко получается применением теоремы Лагранжа. Определение 1. Функция y f x в точке

x1 имеет максимум, если для всех x из
некоторой	-окрестности	точки	x1
выполняется	неравенство f x f (x )		при
		1
x x1.		y f x в точке
Определение 2. Функция		y f x в точке

x2 имеет минимум, если для всех x из некоторой -окрестности точки x2

Y
0	X

выполняется неравенство

f x

f (x	)
2

при

Определение 3. Точки максимума и минимума функции называются точками экстремума.

Теорема о необходимом условии экстремума дифференцируемой

функции. Необходимым условием экстремума дифференцируемой в точке			c
функции является	f
		c 0.

Доказательство. Пусть точка c				– точка
максимума,	тогда		f (c x) f (c)		0
			x

при x 0	и	f (c x) f (c)		0 при
			x
x 0 . Поскольку
			при вычислении

производной пределы слева и справа должны совпадать, то есть f c 0 .

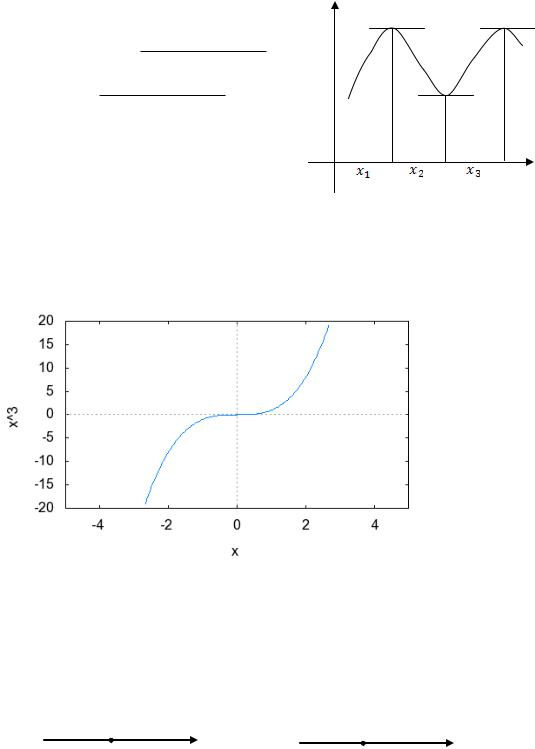
Точки, в которых производная функции обращается в ноль, называются критическими точками.

Критические точки функции не обязательно являются точками экстремума.

Например, если	f x x	3	, то	f ' x 3x	2	0	при

является точкой экстремума, что видно из рисунка.

, но точка

x 0

не

Теорема 1 о достаточном условии существования максимума и

минимума функции.
Если производная функции при переходе через точку c							меняет знак с +
на –,	это точка максимума. Если знак производной меняется с – на +, имеем
точку	минимума. Доказательство			следует	из	теоремы	о возрастании
(убывании) функции.
	+	max	-	-	min	+


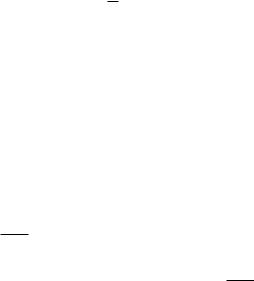
Теорема 2	о	достаточном		условии	существования
минимума функции.		Пусть		0 , тогда при		x x0
			f x0
максимум, если	f " x0 0 и минимум, если				f " x0 0 .

максимума и функция имеет

Доказательство.

Из формулы Тейлора в окрестности точки экстремума

в которой

удержано три первых члена, имеем
y f x f x0 f x0 x x0	1 f x0 x x0 2	o	x x0	2 .
	2
Поскольку f x0 0 , что следует из условия теоремы,			а остаточный член r

по определению меньше предыдущего члена формулы, знак приращения

функции независимо от того,			точка	x	находится левее,				или правее x0 ,
определяется знаком второй		производной.					Когда		0 , получаем
								f x0
f x f x0 0 ,	следовательно,		x0	точка			минимума		функции, если
f x 0, значит	f x f x	0 , тогда x			0	- точка максимума функции.
0	0


П р и м е р 1.			y
как	3	3x		2
	y x

1	x	4	x	3
		4		3
4			(x
x			(x
		2

Найдем критические точки этой функции. Так

, то критическими точками являются

что нет.

0 , x2 3 y x 0

y (x) 0

. Применим первую теорему о достаточном условии. Очевидно,

при x 0	и при 0 x 3, следовательно, в точке 0 экстремума
при x 3	, следовательно, в точке 3 минимум функции.

П р и м е р 2. y cos2 x . Найдем критические точки этой функции. Так как

y sin 2x , то критическими				точками этой функции являются точки
x	k	. Применим вторую теорему о достаточном условии. Очевидно, что
	2
k				k
y (x	) 2cos k , поэтому		x		является точкой локального максимума
				2
k			k

при

четном и точкой локального минимума при

нечетном.

Наибольшее и наименьшее значения функции на отрезке

Следует отличать минимумы и максимумы функций от наибольшего и наименьшего ее значений на заданном отрезке. Функция может не иметь экстремумов в исследуемой области, а наименьшее и наибольшее в этой области значения она имеет всегда.

Чтобы определить наибольшее и наименьшее значения функции на заданном отрезке, необходимо подсчитать значения функции в точках экстремума, входящих в исследуемую область, а также в граничных ее точках и выбрать среди них наименьшее и наибольшее значения.


П р и м е р.							Определить наибольшее и наименьшее значения функции
y x	3	3x			2	1	на отрезке 1; 4 .

Находим точки, в которых производная обращается в нуль:
y 3x			2	6x 3x x 2 0 , получаем две точки, одна из которых				x 0 не

входит в исследуемую область, добавляем к ним граничные точки, тогда

x1 1,	x2 2 ,	x3 4 .
Определяем в этих точках значения функции y1 1,			y2 3 ,	y3 17 .
Таким образом,		наименьшее в заданной области значение функции 3
реализуется при		x 2 , наибольшее 17 при x 3.

ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ

Примерами функций двух переменных являются, например, формулы

		z		x	2		y
эллиптического параболоида,	имеющего уравнение			x			y
эллиптического параболоида,	имеющего уравнение			a	2		b
				a			b

	имеющего уравнение z	x	2	y	2
гиперболическим параболоида,		x		y		.
гиперболическим параболоида,		a	2	b	2	.
		a		b

части приведенных выражений являются функциями переменных

2
2	,		или
2
	Правые
	x	и	y .

Если график функции одной переменной представляет собой плоскую кривую, характеризующую зависимость функции от переменной, то в случае двух переменных такую характеристику зависимости функции ( z ) от переменных ( x и y ) выражает поверхность.

Для графического изображения зависимости функции трех и более переменных понадобилось бы пространство размерности, большей, чем 3. Поэтому такие графические изображения невозможны.

Многомерные пространства.

Мы будем рассматривать	n -мерные пространства	R	n	, элементами которых

являются точки x , каждая из которых задается n координатами (x1, x2,..., xn ) .

В случае малой размерности пространства, чтобы не вводить верхние индексы, мы будем использовать традиционные координаты: x, y, z,u,v, w.

Расстоянием между точками

n -мерного пространства является

величина (x, y) (x1 y1)2 (x2 y2 )2 ... (xn yn )2 .

Функцией

n переменных

,..., x

) , заданной на множестве

z f (x) f (x , x

D из пространства

, назовем закон,

по

которому каждой точке x D

ставится в соответствие вещественное число

z .

Примером функции двух

переменных, заданной на всей плоскости

XOY

, является уже рассмотренная

функция

графическая зависимость

которой изображается с

помощью эллиптического параболоида.

Предел функции многих переменных. Понятие предела функции в точке переносится с функций одной переменной на функции многих

переменных z f (x), x D, следующим	образом. z0	lim f (x) , если для
		x x
		0
любого 0 существует такое значение	( ) 0	, что для любых точек
x D , таких что (x, x0 ) , выполняется неравенство \| f (x) z0 \| .

В случае функций двух переменных для вычисления предела в точке удобно переходить к полярным координатам в окрестности этой точки, а в случае функции трех переменных – к сферическим координатам.

П р и м е р ы. 1. Найти	lim	ln(x ey )		. Переходя к полярным координатам в
	x 1		x2 y2
	y 0

окрестности точки (1,0)

, запишем x 1 r cos , y r sin .

Очевидно, что

точка с координатами

(x, y) стремится к точке с координатами (1,0)

тогда и

только тогда,

когда

r 0.

Следовательно,

искомый

предел

равен

lim

ln(1 r cos er sin )

Последний предел – это предел функции одной

r 0

1 r2 2 r cos

переменной r ,

непрерывной по

r при r 0

для любого значения .

Поэтому мы получаем ответ: lim

ln(x ey )

ln 2 .

x 1

x2 y2

y 0

2. Найти

lim x 0

y 0 z 0

x		2 x y z
	3	2 y	3	z	3

. Переходя к сферическим координатам в

окрестности точки (0,0,0) , положим	x r cos sin , y r sin sin ,
z r cos . Точка с координатами	(x, y, z) стремится к точке (0,0,0) тогда и

только тогда, когда r 0. Следовательно, искомый предел после перехода к сферическим координатам и сокращения числителя и знаменателя на

величину

r	3

равен

. Очевидно, что

данный предел не существует, так выражение не зависит от переменной r Ответ: предел не существует.

как полученное , а зависит только

после сокращения от значений и .

Непрерывность функции многих переменных в точке.

функций одной переменной, функция многих переменных

Как и в случае

z f (x), x D,

называется непрерывной в точке		1
называется непрерывной в точке	x0 (x0
область определения функции D и	f (x	)
	0

Из определения предела функции многих

когда функция	f (x) непрерывна в	точке
такое значение	( ) 0 , что	для

2	n	x0	входит в
, x0 ,..., x0 ) , если точка		x0	входит в
lim	f (x) .
x x
0

переменных следует, что в случае,

x0 , для любого 0		существует
любых точек	x D ,	таких что

(x, x0 ) ,

выполняется неравенство

| f (x) f (x0 ) | . Таким образом,

малым приращениям аргумента (в смысле расстояния в пространстве Rn ) у функции, непрерывной в точке, соответствуют малые приращения

функции.

Как и в случае функций одной переменной, арифметические действия над непрерывными функциями не выводят из класса непрерывных функций, если нет деления на 0.

Дифференцируемость функции многих переменных.

Требование дифференцируемости функции многих переменных в точке является более сильным, чем требование непрерывности функции в точке, так как не только обеспечивается малость приращения функции при малом приращении аргумента. Условие дифференцируемости состоит в том, что


приращение	функции,	соответствующее		бесконечно	малому
приращению	аргумента,	является	результатом		линейного
преобразования этого бесконечно малого приращения аргумента.
Вспомним, что	приращение аргумента		функции многих переменных
является n -мерным вектором,		а линейное отображение n -мерного вектора в
пространство размерности 1		задается матрицей-строкой размера 1 n .

Поэтому условие

дифференцируемости

функции

многих переменных

, x

,...., x

)

в точке

формулируется

z f (x) f (x

(x0

, x0

,..., x0 )

следующим образом: существует матрица-строка (a1,a2,...,an) такая, что

для любого вектора приращений	аргумента			x ( x , x					,..., x	)		имеет
место представление f (x x) f (x ) a x a					x		1	2	n			,
место представление f (x x) f (x ) a x a					x			... an x				,
			1				2				n
0	0	1		2
где величина настолько мала, что		lim							0 .
где величина настолько мала, что	0	lim	) 0	(x		x, x )			0 .
	0	0		(x		x, x )
	(x	x,x			0			0
					0			0

При этом матрица-строка

величина

называется

сравнению с расстоянием

(a ,a		,..., a )
1	2	n

бесконечно

(x	x, x	)
0	0

называется производной матрицей, а малой более высокого порядка по

Частные производные.

Предположим, что функция z f (x) f (x1, x2,...., xn) дифференцируема в

точке

строки

x (x1		, x2,...,
0	0		0
(a ,a			,...,a )
1	2		n

x0n). Как через

выразить элементы производной матрицызаданную функцию? Выберем вектор

приращений так, что приращения происходят только по

k -му аргументу

Вектор приращений аргумента в этом случае имеет

x	k	.

вид

k	,0,...,0)
x (0,0,...,0, x

,следовательно,

(x	x, x	) \| xk
0	0

Приращение

функции

примет

f (x x) f (x ) f (x

,..., x

) f (x ,..., x

) a

lim

0 .

Последние

соотношения

являются

дифференцируемости

функции

g(x

,...x

k 1

, x

k 1

,...,

) f (x

вид , где

условием

x	n	)	одной

0

переменной x

в точке

. При этом

dg(xk )

df (x1

,...xk 1, xk

, xk 1,..., xn )

dxk

x0k

dxk

xk x0k

Таким образом,

k -й элемент производной матрицы-строки является

производной

по

k -й

переменной

заданной функции

точке

при

фиксированных

остальных

переменных

x j x j , j k . Такая производная

называется

частной

производной

функции

многих

переменных

f (x1, x2,...., xn)

по

переменной

точке

x (x1

, x2,..., xn)

обозначается

f (x1,...., xn ) |

f k (x ) .

Итак,

производная

матрица-строка,

x x0

участвующая в определении условия дифференцируемости функции многих переменных в точке x0 (x10, x02,..., x0n), состоит из частных производных по соответствующим переменным в точке x0 :

(a1,a2,...,an) ( fx1 (x0 ), fx2 (x0 ),..., fxn (x0)) .

Главная часть приращения функции многих переменных в точке

принимающая теперь вид

n		k	0			n
		k	0	) x
	f		(x	) x	k
k 1	x					k 1
k 1						k 1

f		(x	) dx	k
f		(x	) dx
x	k	0
x

называется

дифференциалом функции	f (x)	в точке	x0	и обозначается	df (x	) . Таким
					0

образом, связь приращения функции в точке и дифференциала в той же точке

имеет вид	f (x0 x) f (x0 ) df (x0 ) , где	– бесконечно малая более
высокого порядка по сравнению с расстоянием		(x0 x, x0 ) .

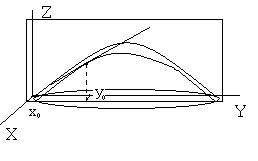
Геометрический смысл частных производных функции двух переменных.

Пусть z f (x, y), x, y D ,	– функция двух переменных. Графическим
изображением этой функции	является поверхность над областью	D .

Рассмотрим точку (x0

, y0 ) D , в которой данная функция имеет конечные

частные производные

fx (x

, y

) и

f y (x , y ) .

Пересечением плоскости

x x0

с заданной поверхностью является кривая.

Аппликата этой кривой

определяется по

формуле

z f (x , y) . Частная

производная

f y (x

, y

)

является

тангенсом

угла

наклона касательной

f (x0, y), лежащей в

плоскости x x0 ,

полученной

кривой

положительным направлением оси OY в точке

y y0

. Направляющий вектор

этой касательной имеет координаты (0,1, f y (x

, y )) .

Пересечением плоскости y y0 с заданной поверхностью является кривая.
Аппликата этой кривой определяется по формуле					z f (x, y0) . Частная
производная	fx (x	, y	) является тангенсом	угла	наклона касательной		к
	0	0	z f (x, y0), лежащей в
полученной	кривой		z f (x, y0), лежащей в		плоскости	y y0 ,	с
положительным направлением оси OX в точке				x x0	. Направляющий вектор
этой касательной имеет координаты (1,0, fx(x				, y )).
			0	0

<<< < Предыдущая 1 2 3 4 56 / 166 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.202570.66 Кб0istoria_zad_otv.doc
#
03.08.2019189.95 Кб14Istoria_zarubezhnoy_literatury_18_veka.doc
#
01.03.202593.11 Кб0Istorii_tamozhennogo_dela_i_tamozhennoy_politik...docx
#
10.02.2015587.33 Кб41istoriya_i_filosofiya_nauki.pdf
#
01.04.202529.52 Кб1ISTORIYa_PEDAGOGIKI_OZO_PSIKh_OBRAZOV.docx
#
10.02.20153.31 Mб21ITIS0.pdf
#
22.04.2019744.45 Кб11itogovaya_baza_testov_po_GMU.doc
#
01.04.2025123.9 Кб0itog_test.doc
#
14.08.20194.53 Mб34ivashkevich_v_b_buhgalterskiy_upravlencheskiy_u...doc
#
22.08.201979.36 Кб6IVF_-_KK_-_Glava_III_-_UDEL_N_J_PERIOD_ROSSIJSK...doc
#
22.08.2019115.2 Кб3IVF_-_KK_-_Glava_IV_-_MOSKOVSKIJ_PERIOD_ROSSIJS...doc