Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ITIS0

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

3.31 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 165 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Примеры получения производных

Применяя замечательные пределы и их следствия, получим

sin x sin a

2sin

x a

cos

x a

sin a lim

lim

x a

sin

x a

lim

lim cos

cosa;

x a 0

x a

cos a lim cos x cosa

2sin

sin

lim

x a

sin

x a

lim

lim sin

sin a;

x a 0

x a

3. (ex ) lim ex ea

|a x a x a

lim	ea (ex a 1)	ea	lim	(ex a 1)	ea ;
	x a			x a
x a			x a 0

ln x ln a

4. ln a lim

lim

x a

x a x a

x a

ln(1

x a

)

lim

;

a x a0

x a

(

)

lim

x a

(

lim

a .

x a 0

ln(1	x a	)
	a

x a

	(	x a		1
		a	1)
	lim
a		x a
	x a

Производные и арифметические операции над функциями

Из условия дифференцируемости и из свойств				пределов
следуют свойства производных.
1. Пусть	функции	f (x) и g(x) дифференцируемы в точке
функция	f (x) g(x)	дифференцируема	в	точке	a	,
( f (x) g(x)) f (x) g (x) .

функций

a . Тогда причем

2. Пусть функция


функция		f (x) дифференцируема в точке a
k f (x)	дифференцируема		в	точке

k R a ,

. Тогда причем

(k f (x)) k f (x) .
3.	Пусть		функции		f (x) и g(x)	дифференцируемы в точке
функция		f (x) g(x)		дифференцируема			в	точке a ,
( f (x) g(x)) f (x) g(x)					f (x) g (x) .
4.	Пусть		функции		f (x) и	g(x)	дифференцируемы в

a . Тогда причем

точке a ,

g(a) 0 .

( gf ((xx)))

	Тогда функция	f (x)
	Тогда функция	g(x)
		g(x)

f (x) g(x) f (x)g (x) . g2 (x)

дифференцируема в точке

, причем

Покажем, как доказывается свойство 3. Обозначим Имеем

h(x)

(x) g(x)

h f (x) g(x) f (a) g(a) ( f (x) f (a)) g(x) f (a) (g(x) g(a))

f g(x) g f (a) ( f (a) x ) g(x) (g (a) x ) f (a)

( f (a) x ) (g(a) g) (g (a) x ) f (a),

где		и – величины более высокого порядка малости,		чем	x .
Раскрывая скобки и собирая коэффициенты при			x ,	получим
следующее представление:
h ( f (a) g(a) g (a) f (a)) x f (a) x g g(a) g f (a)
( f (a) g(a) g (a) f (a)) x ,
где	–	величина более высокого порядка малости,	чем	x .	В

соответствии с условием дифференцируемости и выражением производной свойство 3 доказано.

Упражнение. В качестве приложения свойства 4 докажите равенства:

1		1
tg a		, ctg a		.
	cos2 a		sin2 a

Производная сложной функции

Пусть функция		f (x) дифференцируема
функция	g( y)	дифференцируема в
h(x) g( f (x)) дифференцируема в точке
Доказательство.

в точке точке

x	и h (x
0	0

x0 y0 .

)

,f (x0 ) y0 . Пусть Тогда функция

g (y0) f (x0) .

Имеем

h(x) h(x	) g( f (x)) g( f (x )) g( f (x )) ( f (x) f (x ))
0				0	0		0
g( f (x )) ( f (x		) (x x		) ) g( f (x )) f (x			) (x x	) g( f (x ))
0	0	0			0	0	0	0
g( y	) f (x ) (x x		) ,
0	0	0

где	g( f (x ))	– бесконечно малая величина высшего
	0
малости по сравнению с			(x x	) . Действительно, слагаемое	g(
			0

порядка

f (x0 ))

– бесконечно малая величина высшего порядка малости по сравнению с (x x0 ) , так как сомножитель обладает этим свойством. Слагаемое

– бесконечно малая величина высшего порядка малости по сравнению

с						( f (x) f (x0)) .
								( f (x) f (x		))
lim		(x x		lim		( f (x)		(x x	0
lim			)	lim			f (x ))		)
x x	0		)	x x	0		f (x ))		)
0		0		0			0	0

Таким образом, утверждение доказано.

Поэтому

0 .

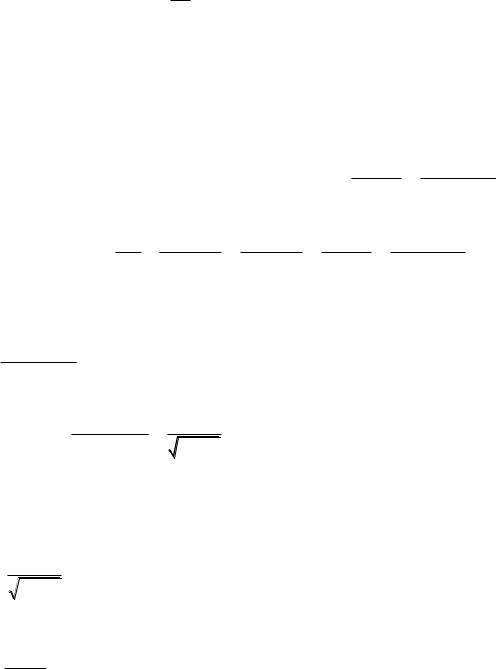
Пример. Найдем производную				ln \| x \|		1		ln
						2

свойством, получим (ln \| x \|)	1	1		2x	1		.
	2	x	2		x

Производная обратной функции

x	2

. Пользуясь доказанным

Даны функция

y f x

и обратная ей функция

x g

Если

f x

дифференцируема

точке

дифференцируема в точке

f (x ), при этом

g ( y

)

Действительно, если x 0 , то

y 0 . Теперь

f '(x

) lim

lim

g '( y

x 0

x 0 x

lim

x 0

y 0

Следовательно,

g ( y

)

f (g( y ))

Пример.

(arcsin x)

cos(sin x)

1 x

y		, т.е.
x		0
	0
	1
(x			)

		0
)			g '(

	x g f
	,тогда
	1
	f (g( y
		0
	1	.
	f (x ))	.
	f (x ))
	0

(x) .
g y
))	.

Упражнение. В качестве приложения правила дифференцирования обратной функции докажите равенства

(arccos x)		1

	1 x
		2
(arc tgx)	1	;
	1 x2

(arcctgx) 1 . 1 x2

;

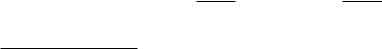
Производная параметрически заданной функции

	x t
Пусть		, t [t	,t		], причем функции
Пусть		, t [t	,t	2	], причем функции
	y t	1		2
	y t

дифференцируемы в точке t0 (t1,t2 ),						(t0 ) 0,

обе функции

(t)

(t0 ) x0 , t0 y0 . Считая,

что y y(x) , вычислим dy в точке x .
					dx			0
					dx
		y				y	lim	y	y '(t0)
y'(x ) lim		y	lim			t	t 0	t	y '(t0)	.
y'(x ) lim			lim				t 0	t		.
0	x 0	x		x 0		x	lim	x	x'(t0)
		x				x	lim	x	x'(t0)
						t	t 0	t
Итак,	y'(x)	y'(t)		.
Итак,	y'(x)			.
		x'(t)

Дифференцирование неявно заданных функций

Если функция задана неявно, перед дифференцированием следует определиться, какую переменную считать аргументом, а затем продифференцировать обе части заданного соотношения, применяя

правило дифференцирования сложной функции.
Пример. Пусть в соотношении				x cos y ln(x y) 5	аргументом
является	x ,	функцией	y . Продифференцируем по		x	заданное
соотношение:		cos y x sin y y (x) 1 y (x) 0 . Отсюда				выражаем
				x y

искомую производную:

y (x)	(x y) cos y 1	.
	(x y) x sin y 1

y (x)(	1	x sin y)	1	cos y
	x y		x y

или

Метод логарифмического дифференцирования

Представим,

(x)	.
y(x) (x)

соотношения:

что нам необходимо взять производную функции Для этого сначала прологарифмируем обе части ln y(x) (x) ln (x) . А теперь продифференцируем обе

части полученного соотношения по x :	y (x)	(x) ln (x)	(x) (x)
	y(x)		(x)

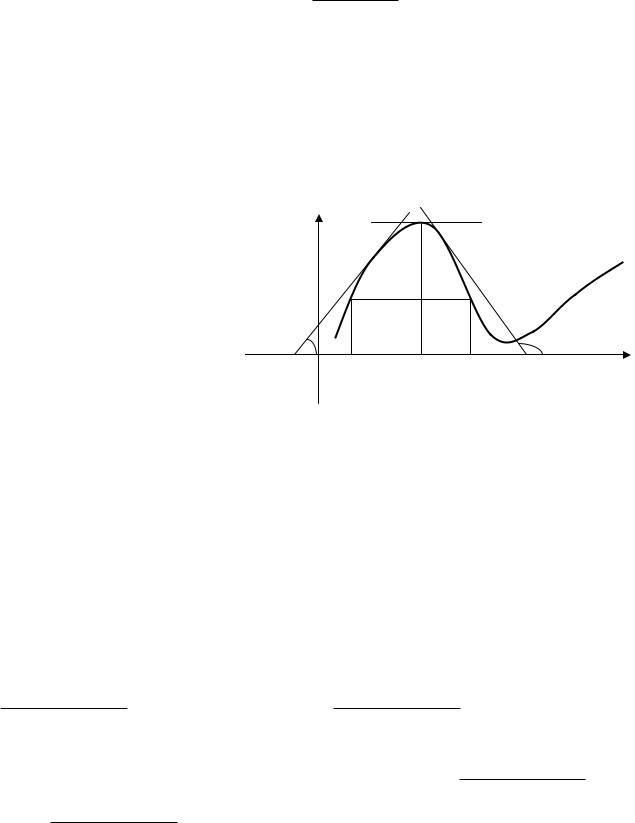
или

y (x)

y(x) ( (x) ln (x)

	(x) (x)	)
	(x)	)
	(x)

Логарифмическое

дифференцирование имеет смысл применять также в случаях, когда необходимо взять производную произведения нескольких функций или производную частного от деления двух произведений.

Теоремы о дифференцируемых функциях

Терема Ролля. Пусть функция
интервала			a , b ,		Y

непрерывна на			отрезке
[a,b] , причем		f a		f b ,
тогда	найдется		хотя	бы
одна	точка	c	внутри
интервала a , b		,	в которой
производная			функции
обращается в нуль, то есть

f c 0, c a , b .

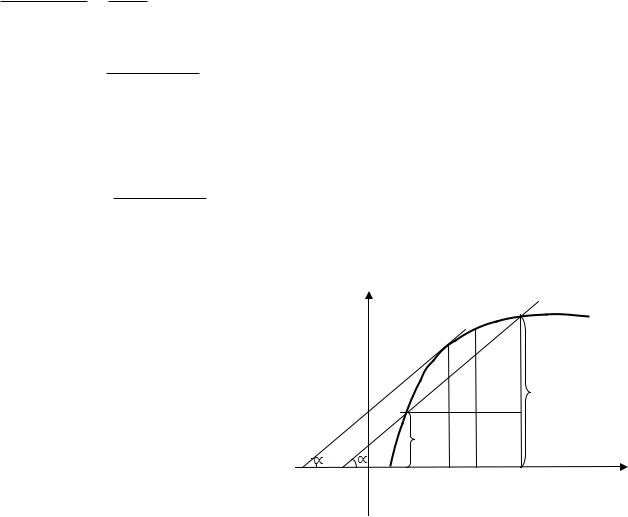
y f x

0 a

дифференцируема внутри

y=f(x)

На рисунке приведена геометрическая иллюстрация теоремы.

Доказательство. 1. В случае, когда теоремы очевиден, и в качестве точки

внутреннюю точку интервала	a , b	.
внутреннюю точку интервала

(x) f (a) f (b)

можно взять

вывод

любую

2. Пусть функция

f (x)

не является постоянной на отрезке

[a,b]

. По

свойству непрерывных на отрезке функций существует внутренняя точка c (a,b) , в которой функция принимает либо минимальное, либо максимальное на отрезке значение. Пусть для определенности это будет

максимальное

значение:

f (x) f (c) 0, x [a,b] .

Значит,

f (c x)x

Поскольку

f (c) 0

функция

при x 0,	f (c x) f (c)	0
	x

f (x) дифференцируема в точке

при x 0 .

с, существует

предел		lim	f (c x) f (c)			f (c) .	Но	lim	f (c

		x 0		x				x 0 0
lim	f (c x) f (c)			0.	Поэтому		единственная
		x
x 0 0

дифференцируемости функции в точке с: f (c) 0.

x) f (c)		,
x	0

возможность

Теорема Коши.					Если функции y f x и y g x
интервале	a , b		и		g b g a , то существует такая
f b f a		f c		.
g b g a		g c

дифференцируемы на

точка

c a , b , что

Доказательство. Рассмотрим вспомогательную функцию

x f

f b f

g x g a .

g b g

y f x и

y g x

Она дифференцируема, так как кроме функций

в нее

входят только постоянные, причем,

a b f a ,

то есть введенная

функция

удовлетворяет

всем

условиям

теоремы

Ролля.

Тогда

f b f a

c f

g b g a

g c 0 , теорема доказана.

Важным частным случаем теоремы Коши при g(x) x является

Теорема Лагранжа.

Если функция

y f x

дифференцируема на

интервале

a , b , то

существует

такая точка c a , b ,

y=f(x)

для которой справедливо:

f b f

a f c b a

f(b)

f(a)

Производные и дифференциалы высших порядков

Определение. Второй производной			функции	y f x

производная ее первой производной	y		.
		y

называется

Если физический смысл первой производной – есть скорость изменения функции, то вторая производная определяет скорость изменения скорости изменения функции, то есть ускорение.


y y ,..., y(n) ( y(n 1) )
Примеры.
1) Если y x5 , то y 5x4 ,	y 20x3 ,	y 60x2 и так далее.

2) Если

y cos

y x ,

sin y

, то

sin x ,	y cos x ,	y	IV	sin x,..., y	(n)	sin(x		n).
			IV		(n)
							2

Аналогично определяются дифференциалы высших порядков. Дифференциал второго порядка – это дифференциал от дифференциала, т.к.

df (x) f (x)'dx , тогда
d	2	f (x) d(df (x)) (df (x))'dx ( f '(x)dx)'dx ,

dx		- бесконечно малое приращение, не зависящее от x, поэтому производная
от него считается как от постоянной. Т.е.
d	2	f (x) ( f '(x))'dx	2	f "(x) dx	2	.

Подобным образом получим d n f (x) f (n) (x) dxn .

Формула Тейлора

Предположим, что функция

y f x

имеет производную первого

порядка в точке a . Из определения дифференцируемости функции в точке a имеем f (a x) f (a) f ' a x , где – бесконечно малая

величина более высокого порядка малости по	сравнению с x при
x 0. Поэтому для точек x , близких к точке a	справедлива формула
f (x) f (a) f ' a (x a),

обеспечивающая первое приближение функции. Эта формула позволяет получать очень грубые приближенные значения функций в точках, так как

ее

можно трактовать как замену функции

f (x) многочленом первой

степени в окрестности той точки

a , где значение функции и ее производной

легко найти. Очевидно, что формула эта применима в очень малой окрестности точки a .

Пример.

4	15	4	16	1	2 4 1	1

						16

	1		3		1
2 1	1			(	1	)
2 1	4	1	4	(	16	)
	4				16

63 32

Здесь мы

использовали формулу				первого приближения при						f (x)	4	1 x,	a 0,

	1					1	3		1
x		. Поэтому	f (a)	1,	f (a)	4	1 4	и (x a)		.
	16								16

Возникают вопросы: 1) нельзя ли использовать многочлены более высоких степеней для более точного приближения функции? 2) как оценить ошибку приближения?

Формула Тейлора дает ответы на эти вопросы.

Предположим, что функция

y f x

имеет все производные до

n 1

порядка в некотором промежутке,

содержащем точку a. В таком случае

для всех значений

из этого промежутка справедлива формула

f x f a

f a

x a

f a

x a

f a

x a

r x ,

n 1

где остаточный член r(x)

(n 1)

(a (x a))

(x a)

и (0,1) .

(n 1)!

Таким образом, функция приближается многочленом, и ошибка вычислений, обусловленная заменой значения функции значением многочлена, равна остаточному члену. Поскольку точное значение (0,1)

не может быть найдено, значения функций вычисляются приближенно, и остаточный член служит не для подсчета, а для оценки ошибки. Последняя формула является обобщением формулы конечных приращений Лагранжа.

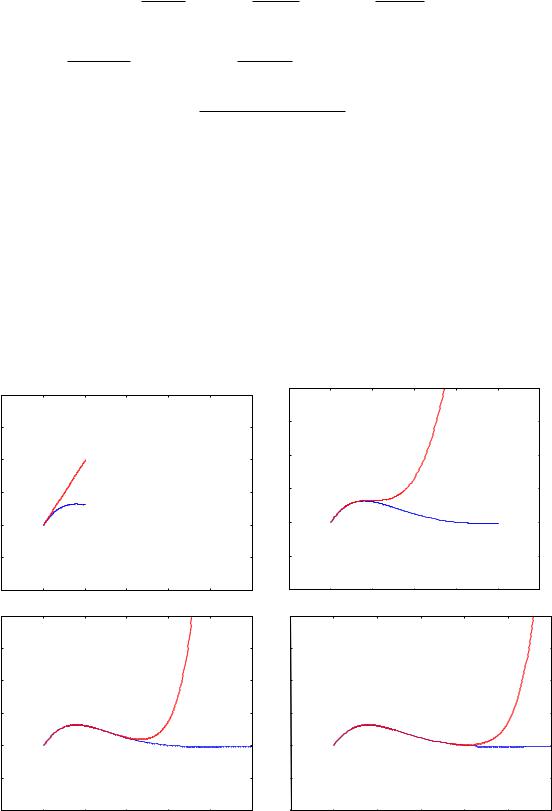
Следующий			пример		демонстрирует,				как	приближается			функция
	x	sin x	(голубая линия) многочленами по формуле Тейлора (красная
f (x) e		sin x	(голубая линия) многочленами по формуле Тейлора (красная
линия) в окрестности точки a 0							при увеличении степеней многочленов от
первой до одиннадцатой.
							2
2
1.5							1.5
1.5
1							1
1
0.5							0.5
0.5
0							0
0
-0.5							-0.5
-1							-1
-1	0	1	2	3	4	5	-1	0	1	2	3	4	5
2							2
1.5							1.5
1							1
0.5							0.5
0							0
-0.5							-0.5
-1							-1
-1	0	1	2	3	4	5	-1	0	1	2	3	4	5

Формулу Тейлора можно записать через дифференциалы:

f a

df (a)

f (a)

f a

d	3

x

f (a)
3!

Для приложений к вычислению пределов используют локальную формулу Тейлора, имеющую вид

x f

x a

f a

x a

f a

4 !

x a

n !

x a

o x a

Такое представление

остаточного

члена

показывает,

что

остаточный

член есть бесконечно малая более высокого порядка малости, чем x a .

Локальная формула Тейлора является обобщением формулы связи

приращения функции и дифференциала функции в точке.

частности, при

a 0

формула

Тейлора

называется

формулой

Маклорена:

f 0

Примеры разложений элементарных функций по формуле Маклорена.

Пример 1.	Рассмотрим функцию	e	x	. Нетрудно	заметить, что					любая

производная	этой функции равна	самой функции,			а	f	n	0 e	0	1. В

соответствии с формулой Маклорена

e	x

	1	x
		1!

Оценим

x	2	x	3

2!		3!

rn (x) :			\|

	x	n	r	x
	x
	n!
	n!		n
			n
r (x) \| e			max{x ,0}
			max{x ,0}
n

| x |n 1 (n 1)!

. В свою очередь для оценки величины

e	max{x,0}	можно брать	1	при
	max{x,0}

Пример 2. Рассмотрим

x 0 и 3x

функцию

при f x

sin

Так

как

f x cos x ,

f x sin x , f x cos x ,			f	IV	x sin x ,		f	V	x cos x
				IV				V
f 0 0 ,	f 0 1 ,	f 0 0 ,		f 0 1 ,		f	IV		0 0 ,	f
							IV

Первые члены формулы Маклорена принимают вид

и т.д., получим

V	….
0 1

sin x 11! x 31! x3 51! x5

<<< < Предыдущая 1 2 3 45 / 165 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.202570.66 Кб0istoria_zad_otv.doc
#
03.08.2019189.95 Кб14Istoria_zarubezhnoy_literatury_18_veka.doc
#
01.03.202593.11 Кб0Istorii_tamozhennogo_dela_i_tamozhennoy_politik...docx
#
10.02.2015587.33 Кб41istoriya_i_filosofiya_nauki.pdf
#
01.04.202529.52 Кб1ISTORIYa_PEDAGOGIKI_OZO_PSIKh_OBRAZOV.docx
#
10.02.20153.31 Mб21ITIS0.pdf
#
22.04.2019744.45 Кб11itogovaya_baza_testov_po_GMU.doc
#
01.04.2025123.9 Кб0itog_test.doc
#
14.08.20194.53 Mб34ivashkevich_v_b_buhgalterskiy_upravlencheskiy_u...doc
#
22.08.201979.36 Кб6IVF_-_KK_-_Glava_III_-_UDEL_N_J_PERIOD_ROSSIJSK...doc
#
22.08.2019115.2 Кб3IVF_-_KK_-_Glava_IV_-_MOSKOVSKIJ_PERIOD_ROSSIJS...doc