
ITIS0
.pdf
|
|
|
|
||||||
и y 9 x2 , x [ 3,3]. |
График первой функции представляет верхнюю |
||||||||
полуокружность, график |
второй – |
|
нижнюю |
ее часть. Если не требовать |
|||||
непрерывности, то из соотношения |
x |
2 |
y |
2 |
9 |
можно получить бесчисленное |
|||
|
|
||||||||
множество функций, заданных на отрезке [-3,3].
|
|
|
|
|
|
|
Кроме того, |
возможно параметрическое задание |
функции |
x t |
, |
||
|
||||||
|
|
|
|
|
y t |
|
|
|
|
|
|
|
|
когда вводится |
дополнительный параметр |
t [t0 |
,T ]. Примером является |
|||
параметрическое |
уравнение той же, |
что |
и |
выше окружности |
||
x 3cost |
,t [0,2 ) |
|
y 3sint |
||
|
, в неявном виде записанное как
x |
2 |
y |
2 |
|
|
9
.
Числовые последовательности.
Числовой последовательностью называют счетный набор пронумерованных
чисел |
xn , n N . Последовательность |
также можно |
рассматривать как |
|
функцию, заданную на множестве |
N. Число xn |
называют членом |
||
последовательности, n – номером этого члена последовательности. |
||||
Примеры. 1) 1 ,n N , 2) 3n, n N , 3)1 ( 1)n , n N , 4) |
( 1)n, n N . |
|||
|
n |
n |
2 |
|
|
|
|
||
|
|
|
|
|
Легко заметить, что члены первой и третьей последовательностей с ростом n приближаются к конкретной величине, члены второй последовательности безгранично увеличиваются, а члены четвертой последовательности поочередно принимают два значения.
Введем определение предела последовательности, используя кванторы общности и существования для отображения динамики процесса.

Определение. Число |
a |
( a lim xn ), если для n
называется
0 |
|
пределом последовательности xn , n N ,
N N( ) N такое, что при n N( )
справедливо неравенство:
| x |
a | |
n |
|
.
Пример.
| x |
a | |
n |
|
Покажем, что |
lim |
|
( 1)n |
||||
1 |
n |
2 |
|||||
|
|
|
n |
|
|||
|
|
|
|
|
|||
1 |
, найдем такое значение |
||||||
n |
2 |
||||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
1. |
|
|
|
|
N( ) |
|
Здесь |
xn |
, что при
1n
( 1) |
n |
||
, |
|||
n |
2 |
||
|
|||
|
|
||
N( ) |
|||
a
(
1
1 |
|
n |
2 |
|
|
. Так как
). Так
как последнее неравенство эквивалентно неравенству
можно принять наибольшее целое число, меньшее или
число обозначается как [ |
1 |
]. |
|
|
|||
|
|
n |
1 |
|
|
||
|
равное
, за
1 |
. |
|
|
||
|
N( )
Такое
Элементарные свойства пределов |
|
|
|
|
|
|||||
1. Предел единственен. |
|
|
|
|
|
|
||||
Доказательство . Пусть a lim xn и |
b lim xn . Для |
0 |
найдем N ( ) |
|||||||
|
|
|
n |
|
n |
|
|
1 |
|
|
такое, что | xn a | |
при n N1( ) |
и найдем N2 ( ) |
такое, |
что | xn b | |
||||||
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|||
при |
n N2 ( ) . |
|
Тогда |
при |
n max{N1( ), N2 ( )} |
получим |
||||
| b a | | b xn xn a | | b xn | | |
xn a | . Из произвольности |
получаем: |
||||||||
расстояние между числами a и |
b может быть сделано сколь угодно малым. |
|||||||||
Это означает, что a b . |
|
|
|
|
|
|
||||
2. Пусть |
xn yn zn, n N . Если |
|
||
(Теорема о двух полицейских). |
|
|||
Доказательство. Для |
0 найдем |
|
||
|
|
|
|
|
n N1( ) и найдем |
N2 ( ) такое, что |
| |
||
|
lim xn |
|
n |
|
N ( ) |
|
1 |
z |
a | |
n |
|
lim zn a ,
n
такое, что
при n
то |
|
| x |
|
|
n |
N |
( |
2 |
|
lim y |
|
n |
n |
|
|
a | |
|
) . Тогда |
|
a .
при
при
n max{N ( ), N |
( )} |
|
1 |
2 |
|
получим |
неравенства |
a xn, zn a . |
Следовательно, при a xn yn zn a
n N( ) max{N ( ), N |
( )} |
|
1 |
2 |
|
, что обеспечивает неравенство | yn
справедливо
a | .
|
|
|
|
1 |
1. Обозначим |
|
Пример применения. Покажем, что lim n |
n |
|||||
|
|
|||||
|
|
n |
|
|
|
|
yn 0, n N . В соответствии с формулой бинома |
||||||
n (1 y )n 1 ny |
n(n 1) y2 |
... yn . |
||||
n |
n |
2! |
n |
|
n |
|
|
|
|
|
|
|
|
1
yn nn 1. Имеем

Следовательно, n 1 |
n(n 1) |
2 |
или y |
2 |
. Из соотношения 0 y |
|
|
2 |
, |
||||||||||
|
2 |
yn |
n |
|
n |
||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|||||
применяя теорему о двух полицейских, получим |
lim yn 0, откуда следует |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
1 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim nn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Пусть xn 0 |
при |
n N . Если |
lim xn a , то a 0 . |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
Доказательство |
от противного. Пусть a 0 . В соответствии с определением |
||||||||||||||||||
предела при |
a |
найдем |
N0 N такое, что |
n N0 (| xn a | |
a |
). То |
|||||||||||||
2 |
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
есть a x a a |
|
при |
n N |
0 |
. Из правого неравенства следует |
x |
|
a , |
|||||||||||
2 |
n |
|
2 |
|
|
|
|
|
|
|
|
|
n |
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
что противоречит предположению.
4. Если lim xn |
a , то lim |
| |
n |
n |
|
Доказательство. |
Сначала |
|
|| xn | | a || | xn a |. Имеем |
|
|
xn | | a |. |
|
|
получим |
вспомогательное |
неравенство |
|
|
|
|
x |
| | a x |
| | x |
| |
|
|
| x |
| | a x |
| |
|
||
| a | | a x |
| a | |
|
|||||||||||||
|
|
|
n |
n |
|
n |
n |
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
| x |
| | x |
a a | | x |
a | | a | |
|
| x |
| | a | | x |
a | |
|
||||||
n |
n |
|
|
n |
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|| x |
| | a || | x |
n |
n |
a
|
.
Согласно определению предела для 0 N N( ) N такое, что при
n N( ) |
справедливо |
неравенству |
при тех же |
Следовательно, |
lim |
| xn | | |
|
n |
|
неравенство: |
| xn a | . Согласно |
|
n N( ) |
справедливо неравенство: |
|
a | . |
|
|
доказанному
|| xn | | a || .
Для рассмотрения следующих свойств пределов последовательностей введем два определения.
Определение |
1. Последовательность |
xn , n N , называется |
ограниченной, |
|
если M 0 |
тчо | xn | M , n N . |
|
|
|
Определение 2. Последовательность |
xn , n N , называется бесконечно малой |
|||
величиной (б.м.в.), если lim xn 0. |
|
|
|
|
|
n |
|
|
|
5. Если последовательность xn , n N , сходится, то есть, |
lim xn a , то |
|||
|
|
|
|
n |
xn , n N , – ограниченная величина.
Доказательство. В соответствии с определением предела при 1 найдем
такое |
N N , |
что | x a | 1 |
при n N |
. Следовательно, в соответствии с |
||||
|
1 |
n |
|
1 |
|
|
|
|
неравенством, |
полученным |
выше, |
|| xn |
| | a || 1 |
при |
n N |
. Отсюда |
|
|
|
|
|
|
|
|
1 |
|
| xn | 1 | a | при n N1. Найдем теперь
M
max{| x |,| x |
|,...,| x |
|
1 |
2 |
N ( ) |
|,| a |
1}
.
Очевидно, что | xn | M , n N .

6. Пусть |
xn , n N , – ограниченная |
величина, |
yn , n N ,– б.м.в. Тогда |
|||||||||||
zn xn yn, n N , – б.м.в. |
|
|
|
|
|
|
|
|
|
|||||
Доказательство. Найдем |
для |
0 |
такое |
N( ) N |
, |
|
что |
n N( ) |
||||||
(| yn | |
|
|
). Тогда для n N( ) выполняется неравенство |
| zn | | xn yn | , то |
||||||||||
M |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
есть lim zn 0 . |
|
|
|
|
|
|
|
|
|
|
||||
n |
|
|
|
|
|
|
|
|
|
|
|
|||
7. Пусть xn , n N , – б.м.в., |
yn , n N ,– б.м.в. Тогда zn xn yn, n N , б.м.в. |
|||||||||||||
Доказательство. Найдем |
для |
0 |
такое |
N1 |
( ) N |
, |
|
что |
n N1( ) |
|||||
(| xn | |
|
) |
и такое |
N2 ( ) N , |
что n N2 |
( ) |
(| yn | |
|
) . |
Тогда при |
||||
2 |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
n N( ) max{N ( ), N |
( )} |
|
1 |
2 |
|
(
| z |
| |
n |
|
).
Арифметические свойства пределов
Для упрощения доказательств этих свойств приведем новое предела последовательности, эквивалентное данному выше:
число |
a |
называется |
пределом последовательности |
xn , |
|||
x |
a x |
|
x |
|
|
|
|
n |
|
n , |
где |
n |
– |
б.м.в. (Доказать эквивалентность |
|
самостоятельно).
определение
n N , если определений
1.Если
lim x |
a |
|
n |
n |
|
|
|
|
и lim yn n
b
, то
lim(x |
|
|
n |
n |
|
|
|
|
y |
) |
n |
|
a b
.
Доказательство. Так как |
x |
a x |
и |
y |
n |
n |
n |
причем выражение в скобках – б.м.в. свойству.
b y |
x |
y |
a b (x |
y ) |
, |
n , то |
n |
n |
n |
n |
согласно седьмому элементарному
2. Если |
lim xn a |
и |
lim yn b , то |
lim(xn yn ) a b . |
|
|||||
|
|
n |
|
n |
|
|
|
n |
|
|
Доказательство. |
|
Так |
|
как |
|
x a x |
и |
|||
|
x |
|
n |
n |
||||||
x |
y a b (b x |
a y |
y ) |
, |
причем |
выражение |
||||
n |
n |
n |
|
n |
n |
n |
||||
согласно шестому и седьмому элементарным свойствам.
y |
b y |
то |
|
n |
|
n , |
|
в скобках |
– |
б.м.в. |
|
3. Если |
lim xn a и a 0 |
|
n |
Доказательство. Так как
|
| x |
| |
|
что выражение |
n |
|
|
| a || x |
a | |
||
|
|||
|
n |
|
|
достаточно показать, |
что |
||
, то lim |
1 |
|
1 |
|
. |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|||||
|
n x |
|
|
|
|
|
|
|
|
|||
|
|
n |
|
|
|
|
|
|
|
|
|
|
x |
a x |
|
|
|
|
1 |
|
1 |
|
| x |
| |
|
|
|
|
|
|
|
n |
|
|
||||
n |
n , |
то |
|
|
|
|
|
|
|
. Чтобы показать, |
||
|
x |
|
a |
|
| a || x a | |
|||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
n |
|
|
|
n |
|
|
– б.м.в., согласно шестому элементарному свойству
1 |
|
– ограниченная величина при достаточно |
|
|
|
|
|
| x a | |
|||
|
n |
|
|
больших значениях n N . Имеем |
1 |
|
|
1 |
|
|
1 |
. Пусть |
|
|
|
|
|
||||
| x a | |
| ( x ) a | |
|| a | | x || |
||||||
|
n |
|
n |
|
n |
|
||
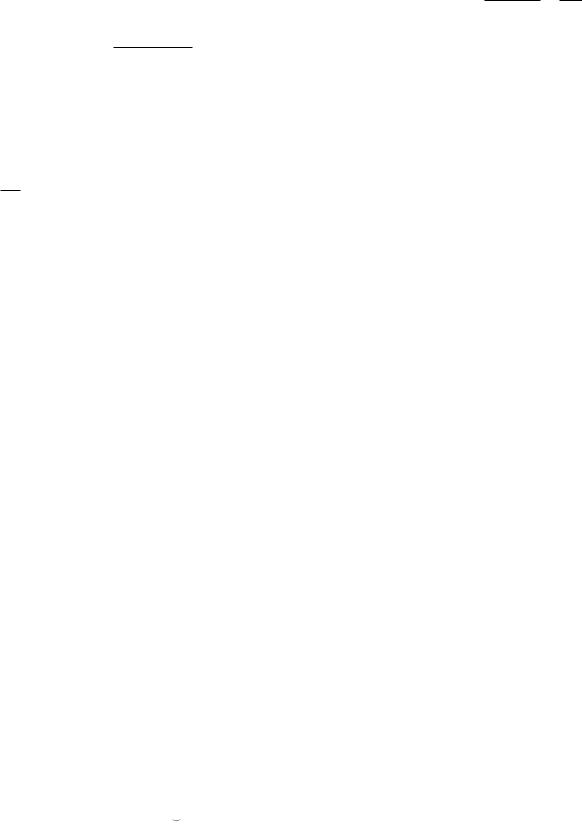
число |
N |
N |
таково, что |
| x |
| |
||
0 |
|
n |
|
||||
при n N0 |
|
| x |
| |
|
|||
и |
n |
a | |
– |
||||
| a || x |
|||||||
|
|
|
|
|
|||
|
|
|
|
n |
|
|
|
| a | |
при n N0 |
|
2 |
||
|
б.м.в. Теперь
. Следовательно, |
1 |
|
2 |
|
a | |
| a | |
|||
| x |
|
|||
n |
|
|
|
остается применить шестое
элементарное свойство и новое определение предела.
Следствие. Согласно 2-му и 3-му арифметическим
является |
следующее утверждение: если |
lim xn |
|||
|
|
|
|
|
n |
|
y |
|
b |
|
|
lim( |
n |
) |
|
. |
|
x |
a |
|
|||
n |
|
|
|
||
|
n |
|
|
|
|
свойствам очевидным
a 0 |
и |
lim yn b , то |
|
|
n |
Основные свойства пределов последовательностей
Прежде, чем сформулируем первое основное свойство, дадим новое
Определение. |
Последовательность |
xn |
, k N , |
называется |
|
|
|
k |
|
|
|
подпоследовательностью последовательности |
xn , n N , если |
n |
, k N , – |
||
|
|
|
|
k |
|
монотонно возрастающая последовательность натуральных чисел. Например,
x |
, x |
, x |
|
,..., x |
k 1 ,.... |
– подпоследовательность последовательности |
|
3 |
7 |
23 |
|
3 4 16 ... 4 |
|
|
|
x , x |
, x |
, x |
,....., xn,... . |
|
|||
1 |
2 |
3 |
|
4 |
|
|
|
1.Из любой ограниченной последовательности можно выбрать сходящуюся |
|
подпоследовательность. |
|
Доказательство. Любая последовательность |
xn , n N , содержит бесконечное |
(счетное) множество |
членов, однако значения некоторых из них могут |
|||
совпадать, например, |
в случае последовательности |
( 1) |
n |
, n N . Обозначим |
|
||||
через A множество значений, принимаемых членами последовательности. Множество A не более, чем счетно. Рассмотрим 2 случая: а)A конечно и
б)A бесконечно.
В случае а) бесконечное множество членов последовательности xn , n N , принимает хотя бы одно значение из A. Обозначив соответствующие члены
последовательности в порядке возрастания номеров |
xn |
, k N , мы получим |
|
k |
|
подпоследовательность, все члены которой принимают единственное значение, и значит, сходятся к этому же значению.
В случае б) множество A является бесконечным ограниченным множеством, и следовательно, согласно теореме Вейерштрасса обладает хотя бы одной
предельной точкой |
a . Согласно определению предельной |
точки в |
проколотой окрестности U1(a) содержится хотя бы одна точка из |
множества |
|
A, а соответствующее значение принимает член последовательности xn1 . Возьмем теперь множество A1 , полученное выбрасыванием из множества A чисел, значения которых принимают все члены последовательности xn с

номерами от |
|
первого |
до |
n . |
Отбрасывание конечного числа членов не |
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
сделает A |
конечным, |
кроме того, точка |
a будет предельной точкой и для |
||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
множества |
A |
. Поэтому в проколотой окрестности |
U1 |
(a) |
найдется число, |
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
значение которого принимает член последовательности |
xn |
, |
причем n n . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теперь отбросим из множества A |
те числа, значения которых принимают |
||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
все |
члены |
последовательности |
xn с |
номерами от |
n 1 |
до |
n . Получим |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
множество |
A |
2 |
, бесконечное и с предельной точкой |
a . Теперь в проколотой |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
окрестности |
U1 (a) найдется число, |
значение которого |
принимает |
член |
|||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
последовательности x |
, причем |
n n |
….. Таким образом, мы построили |
||||||||||||||
|
|
|
|
|
n3 |
|
|
|
2 |
3 |
|
|
|
|
|
|
|
подпоследовательность |
xn |
, k N |
, последовательности |
xn , n N , такую что |
|||||||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
| xn |
a | |
1 |
. |
Из первого |
следствия |
Принципа Архимеда |
следует, |
что |
|||||||||
k |
|||||||||||||||||
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim xn a |
. Итак, сходящаяся подпоследовательность построена. |
|
|||||||||||||||
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Любая монотонная ограниченная последовательность сходится.
Доказательство. Пусть последовательность |
xn , n N , неубывающая, то есть, |
n N (xn xn 1) . Вследствие ограниченности множества значений членов последовательности A существует supA . Согласно второму свойству
супремума для 0 x |
|
такое, что x |
|
|
. В силу монотонности |
||||
|
N |
|
|
N ( ) |
|
|
|
||
для |
n N( ) ( x |
|
xn ) . |
Следовательно, |
для |
||||
|
|
|
N ( ) |
|
|
|
|
|
|
n N( ) (| xn | ) , |
что |
согласно определению |
предела |
доказывает: |
|||||
lim xn . |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
3. Лемма о вложенных отрезках. |
|
|
|
|
|
||||
Пусть |
an ,n N, и bn ,n N, – последовательности концов последовательно |
||||||||
вложенных друг
lim(bn an ) 0 . n
вдруга отрезков
|
|
|
] {a}. |
Тогда |
[a |
,b |
|
|
k |
k |
|
|
k 1 |
|
|
([an,bn ] [a |
,b |
|
]), причем |
n 1 n 1 |
|
||
(То есть, |
|
пересечением |
|
последовательно вложенных друг в друга отрезков с длинами, стремящимися к нулю, является точка).
Доказательство. Очевидно, что последовательности an ,n N, и bn ,n N,
монотонны, причем первая неубывающая, а вторая невозрастающая. Первая ограничена сверху (например, числом b1 ), вторая – снизу (например, числом
a ). Согласно второму основному свойству lim a |
a и lim b |
b . Имеем |
||||||||
1 |
|
|
|
|
n |
n |
|
n |
n |
|
b lim b lim(b a |
a ) lim(b a ) lim a |
a . |
Таким |
|
образом, |
|||||
n n |
n n n |
n |
n n |
n |
n n |
|
|
|
|
|
предельный отрезок, лежащий во всех отрезках, вырождается в точку a . Из

условия последовательной вложимости отрезков
|
|
] lim |
n |
|
] lim[an,bn ] a . |
[a |
,b |
[a |
,b |
||
k |
k |
n |
k |
k |
n |
k 1 |
|
|
k 1 |
|
|
n |
|
[a |
,b |
k |
k |
k 1 |
|
]
[a |
,b |
] |
n |
n |
|
. Поэтому
Неперово число
Утверждение.
lim(1 n
1 |
) |
n |
|
||
n |
|
|
|
|
.
Рассмотрим |
последовательность |
xn (1 |
1 |
) |
n |
, |
|||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
n |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
бинома |
|
Ньютона, |
представим |
|
общий |
|
член |
||||||||||||||||||||||
x 1 |
n |
|
n(n 1) |
|
n(n 1)(n 2) |
... |
|
n! |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
n |
|
|
|
|
||||||||||
n |
|
|
n |
|
|
|
2 n |
|
|
|
2 3 n |
|
|
|
n! n |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
1 |
(1 |
|
1 |
) |
1 |
(1 |
1 |
)(1 |
2 |
) |
... |
1 |
(1 |
1 |
)(1 |
|
2 |
) |
||||||||||
2 |
n |
3! |
n |
n |
n! |
n |
n |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
n N . Пользуясь формулой
последовательности в виде
... (1 |
n 1 |
|
n |
). |
|
|
|
|
Очевидно, что все слагаемые после
положительные, их число равно |
n |
||
слагаемые будут увеличиваться, а |
|
||
добавляться новые, |
то есть |
xn растет |
|
последовательности |
xn |
сверху |
с |
геометрической прогрессии:
числа |
2 в последнем выражении |
||
1 и |
при увеличении |
n |
сами |
кимеющимся слагаемым будут
сростом n . Оценим общий член
применением формулы суммы
x 2 |
1 |
|
1 |
|
... |
1 |
|
2 1 |
|
1 |
|
1 |
... |
1 |
|
|||
|
|
|
|
|
|
|||||||||||||
n |
|
|
2! 3! |
|
|
n! |
2 |
|
2 2 23 |
|
2n 1 |
|||||||
|
|
|
|
|
|
|
||||||||||||
2 |
1 |
|
1 (1/ 2)n 1 |
2 |
1 3. |
|
|
|
|
|
|
|
||||||
2 |
1 1/ 2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, наша последовательность монотонно возрастает и ограничена сверху. Следовательно, в соответствии со вторым основным свойством пределов числовых последовательностей существует предел
этой последовательности, который принято обозначать |
e . Это число |
называется неперовым числом, находится между числами 2 и 3 и приблизительно равно 2,71828.
Итак, lim(1 1)n e .
n n
Критерий Коши сходимости числовой последовательности
Определение предела |
последовательности предполагает известным предел |
последовательности |
( a ), с которым сравнивается общий член |
последовательности
(
xn
).
Возникает вопрос: как узнать, имеет ли
последовательность какой-либо предел, не имея представления о значении этого предела. Ответ на этот вопрос дает
Критерий Коши. |
Последовательность xn, n N, сходится тогда и только |
||||
тогда, |
когда |
для |
0 N N( ) N, такое |
что |
для |
m,n N( )
(| xn
xm
|
)
. (Мы видим,
что сравниваются не общий член
последовательности и предел, а два члена последовательности с достаточно большими номерами. Условие, приведенное в формулировке критерия Коши называется условием фундаментальности последовательности).
Доказательство. |
|
1. Необходимость. Пусть |
lim xn a , то есть, последовательность сходится. |
|
n |
Докажем ее фундаментальность. В соответствии с определением предела для |
||||||||||||
0 N( ) N |
тчо |
для |
n N( ) (| xn a | |
|
). |
Возьмем |
любые |
|||||
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
m,n N( ). Тогда |
| xn xm | | xn a a xm | | xn a | | xm a | |
|
. То |
|||||||||
2 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
есть из сходимости следует фундаментальность. |
|
|
|
|
|
|
|
|
||||
2. Достаточность. |
Пусть |
последовательность |
xn, n N, |
фундаментальна. |
||||||||
Покажем сначала, что из фундаментальности следует ограниченность. В
условии фундаментальности примем 1 |
и найдем |
|
N N |
|
такое, что |
||
m,n N (| xn xm | 1) . |
Следовательно, |
при |
m N 1 |
имеем: |
|||
(| x |
xn | ) при n N . Из неравенства |
|| xn | | x |
|
|| | x |
xn | 1 при |
||
N 1 |
|
|
N 1 |
N 1 |
|
|
|
n N получим неравенство: | xn | 1 | xN 1 | |
при n N . Следовательно, |
||||||
для |
всех |
членов |
|
| x |
| max{| x |,| x |
|,...,| x |
|
n |
1 |
2 |
N |
последовательности
|,1 | x |
|} |
для |
n N |
N 1 |
|
|
|
справедлива оценка
. Итак, ограниченность
доказана. Воспользуемся теперь первым основным свойством пределов
последовательности и |
выберем из ограниченной последовательности |
|||
xn, n N, сходящуюся |
подпоследовательность xn , k N, где |
lim xn |
a . |
|
|
k |
k |
k |
|
Взяв теперь в условии фундаментальности m nk |
при достаточно больших |
||||
значениях |
k K( ) N , |
получим |
k K( ), n N( ) (| xn xn | ) . |
||
|
|
|
|
|
k |
Переходя |
к пределу |
при |
k в |
последнем |
неравенстве, получим |
n N( ) (| xn a | ) . |
В силу произвольности |
выполнение последнего |
|||
неравенства обеспечивает то, что lim xn a . |
|
||||
|
|
|
n |
|
|
Упражнение. Используя определение предела последовательности, докажите, что если последовательность сходится к конечному пределу, то любая ее подпоследовательность сходится к тому же пределу.
Предел функции в точке
Пусть a – предельная точка множества определения функции
Существуют два определения предела функции в точке: |
b lim f (x) . |
||
|
|
|
x a |
1. |
Определение Гейне: для любой последовательности xn, n N |
||
|
что lim xn a , справедливо: |
lim f (xn ) b . |
|
|
n |
n |
|
2. |
Определение Коши: для |
0 ( ) 0 |
такое, что |
x, | x a | , справедливо (| f (x) b | ) .
f (x) .
, такой
для
Для чего нужны два определения? Первое определение не является конструктивным, так как мы не сможем проверить всевозможные числовые последовательности, сходящиеся к точке a. Однако, это определение очень удобно для построения контрпримеров. Доказывать же существование предела в точке удобно с помощью второго определения.
Для того, чтобы пользоваться двумя определениями, докажем их эквивалентность, то есть покажем, что из условий первого определения следует выполнение условий второго определения и наоборот.
2 1. Пусть справедливы условия второго определения и пусть |
lim xn a . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|||
Из определения предела числовой последовательности для любого |
0 и |
|||||||||||||||||||||
определенного в соответствии с условием второго предела значения |
( ) 0 |
|||||||||||||||||||||
найдем |
такое |
значение |
N N( ( )) N( ) N , |
что |
| xn a | ( ) |
для |
||||||||||||||||
любого |
n N( ) . Следовательно, в соответствии с условием определения 2 |
|||||||||||||||||||||
| f (xn ) b | при n N( ) . Последнее является установлением того факта, |
||||||||||||||||||||||
что |
lim f (xn ) b . |
То есть выполнение условий второго |
определения |
|||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
обеспечивает выполнение условий первого определения. |
|
|
|
|
|
|
|
|||||||||||||||
1 2 |
доказывается |
от противного. Пусть выполняются |
условия |
первого |
||||||||||||||||||
определения, но условия второго определения нарушаются, то есть, |
0 |
0 |
||||||||||||||||||||
такое, что для 0 |
x |
такое, |
что |
| x |
a | и |
(| f (x |
) b | |
0 |
) |
. В силу |
||||||||||||
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
||
произвольности |
|
0 |
возьмем |
|
1 |
и найдем при каждом значении n N |
||||||||||||||||
n |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
такое значение |
x , что | x a | 1 |
и (| f (xn) b| |
0 |
) . Мы видим, |
что нашли |
|||||||||||||||||
|
|
|
n |
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
xn, n N , |
|
|
|
|
lim xn a |
|
|
lim f (xn ) b . |
||||||||||
последовательность |
такую, |
что |
|
и |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|||
Последнее показывает невыполнимость условий первого определения. Мы пришли к противоречию.
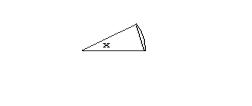
П р и м е р. Покажем, что
limsin x x 0
0
. Пусть
x
0
.
Сравним площади
сектора радиуса 1 раствора |
x |
и вписанного в него равнобедренного |
треугольника с той |
же |
вершиной, |
представленных |
на |
рисунке. |
|||||||
|
|
|
|
Площадь |
треугольника |
равна |
sin x |
, |
||||
|
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
площадь |
сектора |
равна |
|
x |
. |
|||
|
|
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Треугольник вписан в сектор, значит |
||||||||
|
|
|
|
площадь |
треугольника |
меньше |
||||||
площади сектора. Следовательно, sin x x для любого x 0. |
Пользуясь |
|||||||||||
нечетностью функции |
sin x , получим |
sin x x для любого |
x 0 . |
Таким |
||||||||
образом, | sin x | | x | |
для x 0 . Для 0 ( ) |
такое что |sin x | |
||||||||||
при |
| x | ( ) . |
Таким |
образом, |
limsin x 0 |
в соответствии с |
|||||||
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
определением Коши.
Из определения Гейне и свойств пределов последовательностей следует справедливость свойств пределов функций.
Свойства пределов функций
1)если
2)если
3)если
4)если
b lim f (x)
x a
b lim f (x) x a
b lim f (x) x a
b lim f (x) x a
и |
c lim g(x) , то |
b c lim ( f (x) g(x)) ; |
|||
|
x a |
x a |
|
|
|
и |
k R , то kb lim(kf (x)) ; |
|
|
|
|
|
x a |
|
|
|
|
и c lim g(x) , то b c lim ( f (x) g(x)) ; |
|
|
|||
|
x a |
x a |
|
|
|
и c lim g(x) , причем c 0 , то |
b lim( |
f (x) |
) ; |
||
|
|||||
|
x a |
|
c x a |
g(x) |
|
5) если |
f ( |
точки a , то
x)
lim
x a
0 |
при любых |
f (x) b 0 ;
x
, лежащих в некоторой окрестности
6) если |
f |
окрестности
(x) h(x)
точки
g
a ,
(x) |
при |
причем
любых
lim f (x) x a
x ,
lim x a
лежащих g(x) b ,
в некоторой
то lim h(x) b
x a
(теорема о двух полицейских).
П р и м е р. Покажем, что |
limcos x 1. |
Воспользуемся полученной выше |
||||
|
x 0 |
|
|
|
|
|
оценкой в неравенстве 0 | cos x 1| 2sin2 |
|
x |
|
x2 |
. Теперь из теоремы о двух |
|
2 |
|
|||||
|
|
2 |
|
|||
