Файловый архив студентов. Файловый архив студентов.
1305 вузов, 5172 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Казанский федеральный университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

ITIS0

.pdf
Скачиваний:
21
Добавлен:
10.02.2015
Размер:
3.31 Mб
Скачать
☆

Чтобы исследовать, например, траектории, проходящие в квадрате со стороной 20 и центром (0,0) через точки (3,3), (-3,3), (-3,-3), (3,-3), вводим следующие команды: load(drawdf); drawdf([a*x+b*y,c*x+d*y], field_degree=2, duration=20, soln_arrows=true, solns_at([3,3], [-3,3], [-3,-3], [3,-3])) и нажимаем Shift+Enter.

Понятие об устойчивости решения динамической системы

Анализируя поведение траекторий в окрестности положения

равновесия (0,0), мы заметили, что траектории могут

 

а) приближаться к точке

(0,0) с ростом

t

(асимптотическая

устойчивость положения равновесия, примеры – устойчивый узел,

устойчивый фокус),

 

 

б) удаляться от точки (0,0) с ростом

t

(неустойчивость положения

равновесия, примеры – неустойчивый узел, неустойчивый фокус, седло),

в) оставаться вблизи точки (0,0) с ростом

t

(устойчивость положения

равновесия, пример – центр).

 

 

 

 

Теперь представим, что система общего

вида

x f (x, y,t),

имеет

y g(x, y,t),

 

 

 

 

 

 

 

 

 

частное решение

x x

(t), y

 

0

 

 

Введем новые функции

u(t)

функции

 

 

 

 

 

 

 

 

 

y

 

 

 

x

(t) , то есть

0

y

0

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

x(t) x

(t)

и

v(t)

 

0

 

 

 

 

удовлетворяют

f (x

(t),

0

 

g(x

(t),

0

 

y(t) y0

y

(t),t),

0

 

y

(t),t).

0

 

(t) . Тогда новые

 

системе

u f (u x0 (t),v y0 (t),t) f (x0 (t), y0 (t),t),y g(u x0 (t),v y0 (t),t) g(x0 (t), y0 (t),t).

Для новой системы точка (0,0) станет положением равновесия. Хотя новая система не является линейной системой с постоянными коэффициентами,

достаточно рассмотреть линейные по

u

и

v

части выражений в правых

частях системы

в окрестности точки (0,0). В соответствии с поведением

траекторий для

новой системы можно сделать вывод о том, будет ли

решение

x x0 (t), y y0(t)

исходной

системы

устойчивым,

асимптотически устойчивым или неустойчивым.

П р и м е р 1. Найти и исследовать положения равновесия системы

 

x x (1 x y),

 

y y (3/ 4 y x / 2).

Сначала

найдем

положения

равновесия,

решая

систему

 

x (1 x y) 0,

 

 

 

 

 

 

 

 

 

 

 

y x / 2) 0.

 

 

 

 

y (3/ 4

 

 

 

 

 

 

 

 

 

 

 

Очевидно, что решением системы являются точки (0,0), (0,3/4), (1,0) и

(1/2,1/2).

1) Исследуем положение равновесия (0,0). Отбрасывая вблизи этой точки в правых частях уравнений системы нелинейные слагаемые, придем к

 

x x,

 

линейной системе

 

y y 3/ 4.

 

 

Характеристическим уравнением системы является

(1 k) (3/ 4 k) 0 .

Оба корня характеристического уравнения положительны. Следовательно, положение равновесия (0,0) – неустойчивый узел.

2)

Исследуем

положение равновесия (0,3/4). Сделаем замену:

u x, v y 3/ 4.

Отбрасывая нелинейные слагаемые, получим вблизи

точки положения равновесия

 

u u / 4,

 

 

 

 

 

 

v v 3/ 4.

 

 

 

 

 

 

 

Характеристическим

(1/ 4 k) ( 3/ 4 k)

0

уравнением системы является уравнение

. Один из корней характеристического уравнения

положителен, другой отрицателен. Следовательно, положение равновесия (0,3/4) – седло. Устойчивости нет.

3) Исследуем положение равновесия (1,0).

Сделаем замену:

u x 1,

v y . Отбрасывая нелинейные слагаемые,

получим вблизи точки положения равновесия u u,

v v / 4.

Характеристическим

уравнением системы является

уравнение

( 1 k) (1/ 4 k) 0 .

Один из корней характеристического

уравнения

положителен, другой отрицателен. Следовательно, положение равновесия

(1,0) – седло. Устойчивости нет.

 

4) Исследуем положение равновесия (1/2,1/2). Сделаем

замену:

u x 1/ 2, v y 1/ 2 . Отбрасывая нелинейные слагаемые,

получим

u (u v) / 2,

вблизи точки положения равновесия

v u / 4 v / 2.

Характеристическим уравнением системы является уравнение (1/ 2 k)2 1/8 0. Оба корня характеристического уравнения

отрицательны. Следовательно, положение равновесия (1/2,1/2) – устойчивый узел.

Устойчивость положений равновесия заданной системы можно также исследовать графически с помощью того же оператора drawdf.

Например, введение команд load(drawdf); drawdf([x*(1-x-y), y*(3/4-y- x/2)], [x,0,1.1], [y,0,1], field_degree=2, soln_arrows=true, point_at(1/2,1/2), solns_at([0.1,0.2], [0.2,0.1], [1,0.8], [0.8,1], [0.1,0.1], [0.6,0.05], [0.05,0.4], [1,0.01], [0.01,0.75])); дает следующую картину траекторий, проходящих через выбранные точки.

1

0.8

0.6

0.4

0.2

0

0

0.2

0.4

0.6

0.8

1

При этом по полученной картине можно заметить, что положение равновесия (0,0) – неустойчивое, а положение равновесия (1/2,1/2) – асимптотически устойчивое. Для демонстрации устойчивости и неустойчивости приведены частные решения, проходящие через заданные точки (0.1,0.2), (0.2,0.1), (1,0.8), (0.8,1), (0.1,0.1), (0.6,0.05), (0.05,0.4), (1,0.01) и (0.01,0.75).

П р и м е р 2. Исследовать,

y0 (t) 2sin t системы

 

x ln(x 2sin

2

t

)

 

 

 

2

 

 

 

 

 

 

y (4 x

2

)cost 2xsin

 

 

 

 

 

 

 

Введем новые функции вид

 

 

 

v

,

u ln(1 u)

2

 

 

 

 

 

2

cost 2u.

v u

 

 

 

 

 

 

y , 2

2

t cos

3

t.

 

 

u x cost

устойчиво ли решение

x

(t) cost,

 

0

 

,

v y 2sint . Теперь система примет

Последняя система имеет положение равновесия

(0,0)

. Отбрасывая

нелинейные слагаемые в правых частях, получим линеаризованную систему

u u 2v ,

v 2u.

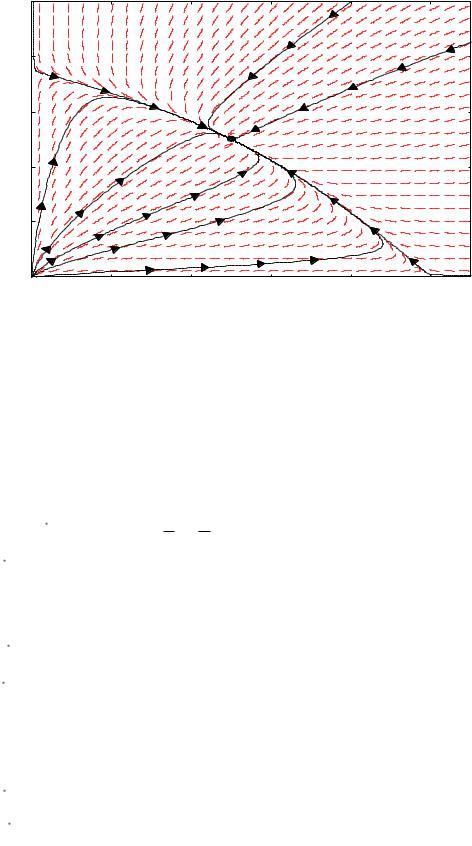
Последняя система имеет характеристическое уравнение

k

2

k 1

0

,

 

один корень которого положителен, а другой отрицателен. Следовательно, соответствующее положение равновесия – седло. Так что данное решение первоначальной системы не будет устойчивым.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности