Применение пакета программ MAXIMA для решения задач Коши для систем линейных дифференциальных уравнений
При решении систем используются те же команды, что и для решения линейных уравнений высших порядков. Например, мы решаем неоднородную систему из предыдущего примера с начальными условиями
y (0) 2, |
y (0) 2 |
. Сначала вводим дифференциальные уравнения: |
1 |
2 |
|
'diff(y1(x),x)=5*y1(x)-3*y2(x)+2*%e^(3*x); 'diff(y2(x),x)=y1(x)+y2(x)+5*%e^(-x);.
Предположим, что первое дифференциальное уравнение записалось под номером %o1, а второе под номером %o2. Теперь введем начальные условия: atvalue(y1(x),x=0,2); atvalue(y2(x),x=0,-2);. Наконец, решаем введенную систему уравнений: desolve([%o1,%o2],[y1(x),y2(x)]);. Ответ имеет вид
[y1(x)=(15*%e^(4*x))/2-4*%e^(3*x)-%e^(2*x)/2-%e^(-x), y2(x)=(5*%e^(4*x))/2-2*%e^(3*x)-%e^(2*x)/2-2*%e^(-x)].
Приближенное решение дифференциальных уравнений.
Класс уравнений, для которых можно получить точное решение, то есть, аналитическую функцию, удовлетворяющую заданному дифференциальному уравнению и всем дополнительным условиям (задача Коши), очень узок. Чаще всего дифференциальные уравнения решаются приближенно. С одним из методов – итерационным – мы познакомились при доказательстве теоремы существования и единственности.
1. Приближение решения с помощью степенного ряда. Представим, что мы должны решить задачу Коши для дифференциального уравнения n -го
y |
(n) |
F(x, y, y ,..., |
|
y (x |
) y ,..., y(n 1) |
(x |
0 |
|
1 |
0 |
сначальным условием
Если функция |
F |
в правой части |
уравнения разлагается в ряды по всем своим переменным, удобно искать
решение дифференциального уравнения в окрестности точки |
x x0 |
в виде |
ряда Тейлора |
по |
степеням |
(x x ) . |
Представим решение |
в |
виде |
|
|
|
|
|
|
0 |
|
|
|
|
y(x) c |
c (x x ) c |
(x x ) |
2 |
.... Из |
начальных условий |
и |
свойств |
|
0 |
1 |
0 |
2 |
0 |
|
|
|
|
|
|
коэффициентов ряда Тейлора следует, что все коэффициенты разложения
вплоть до cn |
нам известны: |
|
|
|
|
|
y(x) y |
y (x x ) |
y2 |
(x x )2 |
... |
yn 1 |
|
(x x )n 1 |
|
|
(n 1)! |
0 |
1 |
0 |
2! |
0 |
|
0 |
|
|
|
|
|
|
|
|
F(x0, y0,..., yn 1) (x x0 )n cn 1(x x0 )n 1 ..., n!
остальные – неизвестные – коэффициенты обозначаются буквами |
c |
и |
|
k |
|
определяются сравнением коэффициентов при одинаковых степенях, находящихся в обеих частях дифференциального уравнения.
м е р. Решить следующую задачу Коши: y xy y2 , y (0) 2 .
Искать решение будем |
в виде ряда |
по |
степеням |
|
начальными условиями |
y(x) 1 2x |
1 |
x |
2 |
c x |
3 |
c x |
4 |
|
|
|
|
|
|
|
2 |
|
|
3 |
|
4 |
|
|
|
|
|
|
|
|
|
хотя бы первые слагаемые рядов в уравнение:
1 6c x 12c |
x2 20c x3 |
... x(2 x 3c x2 |
...) |
3 |
|
|
4 |
|
5 |
|
|
|
3 |
|
(1 2x |
1 |
x2 |
c x3 |
...)(1 2x |
1 |
x2 |
c x3 ...). |
|
|
|
2 |
|
|
3 |
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
Перемножим входящие в правую часть сомножители:
1 6c x 12c x |
2 |
20c x |
3 |
... 2x x |
2 |
3c x |
3 |
... (1 4x 3x |
2 |
(2c |
2)x |
3 |
...) |
|
|
|
|
|
|
3 |
4 |
|
5 |
|
|
|
3 |
|
|
|
3 |
|
|
|
А теперь сравним свободные члены (они равны) и коэффициенты при |
x , при |
x |
2 |
|
|
и |
|
при |
|
x |
3 |
: |
6c |
2, 12c |
4, |
20c |
2c 2 . |
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
|
5 |
3 |
|
c |
|
|
1 |
, |
c |
|
1 |
, |
c |
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
4 |
|
3 |
|
5 |
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мы могли бы и далее сравнивать коэффициенты при степенях x в уравнении
и получать |
значения |
других |
коэффициентов |
c . |
Тем более |
применение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
программ MAXIMA упрощает этот процесс. В данном случае мы получили |
решение |
в |
|
|
виде |
|
|
ряда, |
|
первые члены |
которого |
известны: |
y(x) 1 2x |
1 |
x |
2 |
|
1 |
x |
3 |
|
1 |
x |
4 |
|
2 |
|
x |
5 |
.... |
|
|
|
2 |
|
3 |
|
3 |
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задачу Коши для системы уравнений можно решать подобным способом.
2. Метод Эйлера и его модификации. Познакомимся с методом Эйлера численного решения задачи Коши для дифференциального уравнения
первого |
порядка |
y f (x, y), |
y(x0) y0 . Предположим, |
что |
мы |
должны |
решить |
задачу на |
отрезке |
[x |
, x b]. Разделим отрезок |
[x |
, x b] на n |
|
|
|
0 |
|
0 |
0 |
0 |
|
равных |
частей, |
равных |
. |
Заменим на |
каждом |
отрезке |
[x0 k , x0 (k 1) ] [xk , xk 1], |
k 0,...,n 1, решение дифференциального |
уравнения линейной функцией yk (x) yk f (xk , yk )(x xk ) . При этом имеем
узловые |
|
|
|
|
значения |
|
|
|
|
решения: |
y y |
f (x |
, y |
) , y |
y |
f (x , y ) ,..., y |
y |
f (x |
, y |
) . |
1 |
0 |
0 |
0 |
2 |
1 |
1 |
1 |
n |
n 1 |
n 1 n 1 |
|
Мы здесь приравниваем отношение приращений функции и аргумента производной в точке, соответствующей началу отрезка разбиения:
yk 1 yk f (xk , yk ) .
Очевидно, что такое приближение
мы отойдем от точки |
(x |
, y |
) |
|
0 |
0 |
|
является тем менее точным, чем дальше
. Метод Эйлера является наиболее
примитивным. Здесь интегральная кривая заменяется ломаной, состоящей из прямолинейных отрезков. Возможны его некоторые модификации, несколько улучшающие точность. Например, если брать постоянные значения в виде
Наиболее распространенным численным методом решения указанной задачи Коши является метод Рунге-Кутта. При решении дифференциального уравнения этим методом интегральная кривая заменяется ломаной, состоящей из кусков парабол. Метод Рунге-Кутта встроен в пакет программ
MAXIMA.
Например, мы хотим начальным условием
решить дифференциальное уравнение |
y y |
2 |
x |
с |
|
y(0) 0.3 . При этом мы задаем отрезок [0,1], |
на |
котором хотим получить численное решение и шаг разбиения этого отрезка, равный 0.05. Мы должны ввести команду
load(dynamics); rk(y^2+x,y,0.3,[x,0,1,0.05]);
После того, как мы нажмем клавиши Shift+Enter, получим данные
[[0,0.3],[0.05,0.30583128660202],[0.1,0.31438277172198],[0.15,
0.32574776902574],[0.2,0.34003114365951],[0.25,0.35735268712942],[0.3,
0.37785103897622],[0.35,0.40168830090343],[0.4,0.42905553899765],[0.45,
0.46017943684494],[0.5,0.49533045405802],[0.55,0.53483297195895],[0.6,
0.57907808748734],[0.65,0.62853997325452],[0.7,0.6837970957275],[0.75,
0.74556013793749],[0.8,0.81470931041585],[0.85,0.89234502470182],[0.9,
0.97985793824278],[0.95,1.079027666994073],[1.0,1.192164923146931]].
Это означает, что мы получили узловые значения решения: y(0.05)=
0.30583128660202,…, y(0.4)= 0.42905553899765,…..
Приближенное решение дифференциальных уравнений высших порядков
сводятся к решению систем уравнений первого порядка. Например, требуется решить дифференциальное уравнение y x(y )2 3x2 y 2 на отрезке [0,2] с
шагом |
0.1 |
при начальных |
условиях |
y(0) 1, y (0) 0 . |
Введем новую |
функцию |
z y . Теперь |
уравнение |
запишется в |
виде системы |
|
y z, |
|
|
|
|
|
|
|
|
|
z 2 xz2 |
3x2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с начальными условиями y(0) 1, z(0) 0 .
Для получения решения методом Рунге-Кутта вводим команду load(dynamics); rk([z,2-x*z^2-3*x^2*y], [y,z], [1,0], [x,0,2,0.1]).
Мы получим значения в узлах:
[[0,1,0],[0.1,1.009973277486667,0.19889443755825],[0.2,1.03953179049664,
0.39025908431976],[0.3,1.087443707860848,0.56407930484999],[0.4,1.1513554
76824082,
0.70808296273707],[0.5,1.227625229955781,0.80905909503231],[0.6,1.3113210
0772257,
0.85473889531278],[0.7,1.396404177611673,0.83546996450053],[0.8,1.4760334
30956961,
0.74483368487679],[0.9,1.542855824183935,0.57873490276185],[1.0,1.5891289
45076604, 0.33294944409803],[1.1,1.606518986789783,-9.8829227227875682*10^-4],[1.2, 1.585353126452777,-0.44308261198787],[1.3,1.512758668789601,- 1.041803224981043],[1.4 ,1.367721332806764,-1.927748829187044],[1.5,1.104119674291387,- 3.562685524381777],[ 1.6,0.55276102463945,-9.157645341403534],[1.7,-3.785389000081017,- 789.9052329768924], [1.8,-1.8741633219283803*10^14,-3.7934868677108632*10^30]].
Это означает, что, например, y(0.5)= 1.227625229955781, z(0.5)= 0.80905909503231.
3. Графический метод. Этим методом можно решать дифференциальные
уравнения |
первого |
порядка |
вида |
y f (x, y) . Если |
нам |
необходимо |
построить интегральные кривые, которые являются графиками |
решений |
приведенного уравнения, в какой-то части плоскости |
XOY , |
мы каждой |
точке (x , y ) этой области |
ставим |
в |
соответствие значение |
f (x |
, y ) , |
0 |
0 |
|
|
|
|
|
|
0 |
0 |
которое совпадает с тангенсом угла наклона касательной |
к интегральной |
кривой, проходящей |
через |
точку |
(x |
, y ) . Зная точку |
и направление |
|
|
|
|
0 |
0 |
|
|
|
|
движения по кривой из этой точки, мы переходим к близкой точке, в которой также определяем направление движения,…. Так, двигаясь от точки к точке, мы построим соответствующую интегральную кривую, то есть, решим
задачу Коши |
y f (x, y), |
y(x |
) y . |
|
|
0 |
0 |
Реальное построение решения таким методом было бы очень сложным без применения компьютерной техники. MAXIMA содержит программу построения графических решений. Если мы введем load(plotdf); plotdf(f(x,y),[y,c,d],[x,a,b]), на экране появится прямоугольник [a,b]×[c,d] , в
точках которого указаны направления касательных к интегральным кривым,
проходящим через эти точки. Если щелкнуть курсором по выбранной точке на плоскости, компьютер нарисует интегральную кривую, проходящую через соответствующую точку.
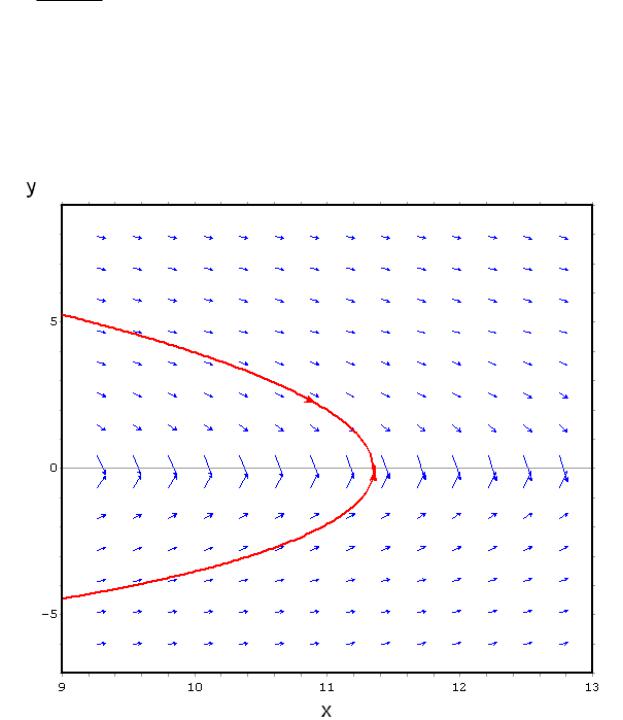
Например, |
|
мы |
хотим построить |
интегральную |
|
5 x |
|
|
|
|
y |
2 |
|
|
|
|
2xy y |
2 |
, |
расположенную в |
прямоугольнике |
|
|
|
|
|
|
|
|
|
проходящую через точку (11,2) .
Введем load(plotdf); plotdf((5-x^2)/(2*x*y-y^2),[y,-7,9],[x,9,13]); и нажмем
Shift+Enter. Мы получим выбранный прямоугольник с указанием направлений из точек прямоугольника. Теперь щелкнем по точке (11,2) , и нарисуется соответствующая интегральная кривая.
Динамические системы
Системы дифференциальных уравнений имеют приложения в физике, |
так как моделируют движение точки в пространстве. Продемонстрируем |
это для случая движения точки с координатами (x, y) |
на плоскости в |
зависимости от времени t . Задать закон движения – |
значит задать |
зависимость скоростей изменения абсциссы x |
и ординаты y от времени и |
местоположения точки на плоскости. Таким |
образом, закон движения |
точки на плоскости в общем случае принимает вид
x f (x, y,t), y g(x, y,t).
системы дифференциальных уравнений называются динамическими
системами. |
Их частные решения |
x x(t), y y(t) |
называются |
траекториями динамической системы. В частном случае, когда траектория вырождается в точку, соответствующее решение называется
точкой покоя или положением равновесия. Очевидно, что в положении равновесия (a,b) имеем f (a,b,t) 0 и g(a,b,t) 0.
Рассмотрим линейные однородные динамические
x a x b y, |
|
|
|
|
x x(t), |
постоянными коэффициентами: |
где |
y c x d y, |
|
|
|
|
|
Нетрудно заметить, что пара вырожденных функций |
x 0, |
системы с
y y(t). y 0 является
частным решением линейной однородной системы и представляет собой положение равновесия. Для исследования поведения других частных решений динамической системы в окрестности положения равновесия
необходимо решить характеристическое уравнение
зависимости от корней траектории системы в
этого уравнения мы окрестности положения
Рассмотрим основные случаи.
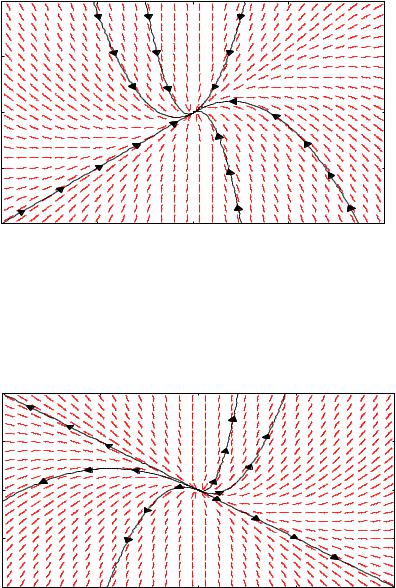
1. Два простых вещественных корня
является
x(t) C1ek1t C2ek2t , y(t) C1 k1 a ek1t b
k |
и |
k |
2 |
. Общим решением системы |
1 |
|
|
|
|
|
|
|
|
|
|
|
вектор-функция |
C |
|
k2 a |
ek2t . |
|
|
2 |
|
b |
|
|
|
|
|
|
|
1-а. k1 k2 0. Очевидно, что с ростом стремятся к положению равновесия
t точки по любой траектории |
(0,0) при |
t , причем |
|
|
|
|
|
|
x(t) C ek2t , |
y(t) |
C |
k2 a |
ek2t . В данном случае положение равновесия |
|
2 |
|
2 |
b |
|
|
|
|
называется устойчивым узлом.
10
5
0
-5
-10
1-б. |
k1 k2 |
0 . |
С ростом t точки по любой траектории удаляются от |
точки |
(0,0) |
. Но |
если устремлять t к , точки по траекториям будут |
стремиться к (0,0) . В данном случае положение равновесия (0,0)
называется неустойчивым узлом.
10 |
|
|
|
|
5 |
|
|
|
|
0 |
|
|
|
|
-5 |
|
|
|
|
-10 |
|
|
|
|
-10 |
-5 |
0 |
5 |
10 |
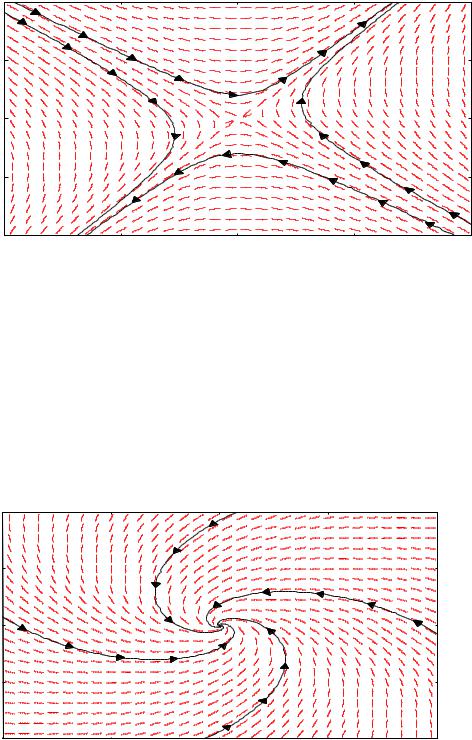
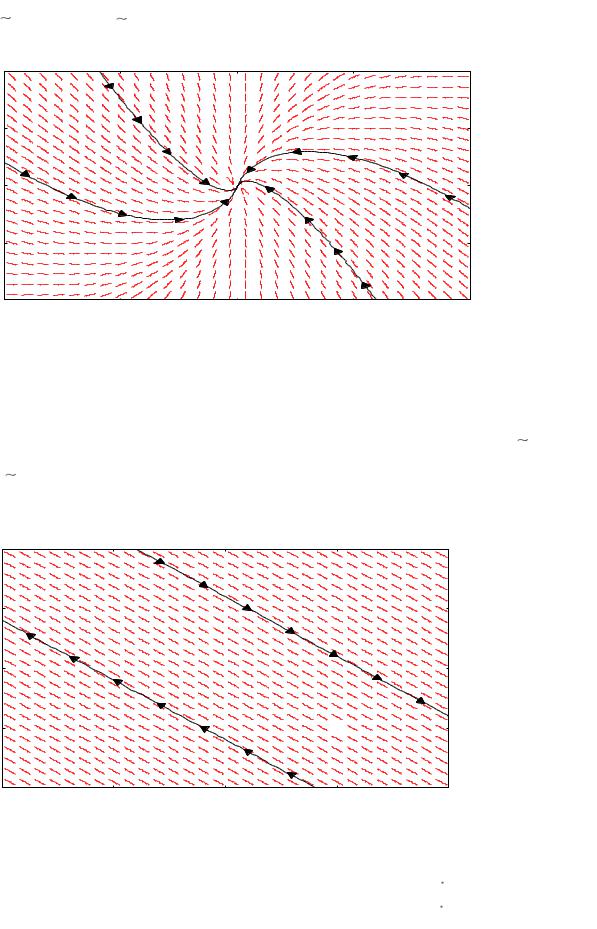
1-в. k1 0 k2 . В этом случае точки по траекториям не могут стремиться к (0,0) , и положение равновесия называется седлом. Оно неустойчиво.
10 |
|
|
|
|
5 |
|
|
|
|
0 |
|
|
|
|
-5 |
|
|
|
|
-10 |
|
|
|
|
-10 |
-5 |
0 |
5 |
10 |
2. Два комплексно-сопряженных корня
решением |
|
системы |
является |
вектор-функция |
t |
(C cos t C sin t) , |
|
|
|
|
x(t) e |
|
|
|
|
|
1 |
|
2 |
|
|
|
|
y(t) e t ( a C1 |
C2 )cos t ( a C2 |
|
C2)sin t . |
|
|
b |
b |
b |
|
b |
|
|
|
|
|
|
|
2-а. 0 . В этом случае с ростом t |
точки по любой траектории стремятся |
к положению равновесия |
(0,0) |
при |
t , при этом вследствие |
присутствия периодических функций траектории описывают вокруг точки
(0,0) |
спирали. Положение равновесия называется устойчивым фокусом. |
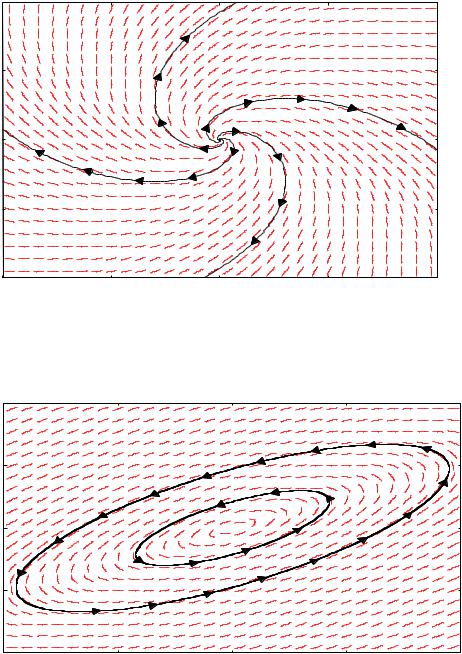
10 |
|
5
2-б. 0. В этом случае с ростом |
t |
точки |
удаляются от положения равновесия, при этом
вокруг точки |
(0,0) |
спирали. Положение |
неустойчивым фокусом.
по любой траектории
равновесия
траектории
описывают
называется
10
5
0
-5
-10 |
|
|
|
|
-10 |
-5 |
0 |
5 |
2-в. |
0. |
В этом случае координатные функции |
периодическими, траектории представляют собой бесконечное число раз обходимые замкнутые кривые – эллипсы. Положение равновесия называется центром.
10
5
0
-5
3. Характеристическое уравнение имеет кратный корень k |
|
. Общим |
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2 |
|
|
|
решением |
системы |
|
является |
|
вектор-функция |
|
x(t) e t (C C t) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
t a |
C |
1 |
C |
a |
|
|
|
|
|
|
|
|
|
y(t) e |
|
|
|
|
C t . |
|
|
|
|
|
|
|
b |
1 |
b |
|
2 |
|
b |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3-а. 0 . |
Очевидно, |
что |
с |
|
ростом t |
точки |
по |
любой траектории |
стремятся |
к |
положению |
равновесия |
(0,0) |
при |
t , |
причем |