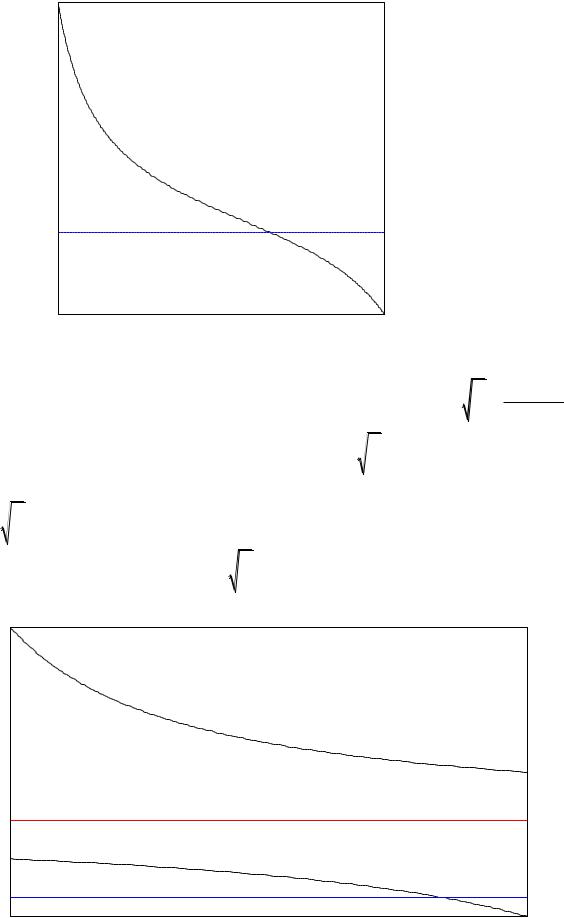
функции. Если брать частную сумму с большим количеством членов, то график частной суммы будет теснее приближаться к исходной функции во
внутренних точках интервала |
(- , ) , но вблизи точек |
x |
поведение |
будет тем же из-за разрыва исходной функции при периодическом продолжении.
Мы видим, что если задать функцию на симметричном интервале
то ряд Фурье, построенный для этой функции, автоматически продолжает
|
исходную |
функцию |
T периодически |
на всю |
вещественную |
|
ось. |
|
Оказывается, можно задать функцию на полуинтервале [0, |
T |
) , продолжить ее |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
четным или нечетным образом на симметричный полуинтервал |
( |
T |
,0] и |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уже затем |
продолжить |
полученную на |
интервале |
( |
T |
|
, |
T |
) четную |
или |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
нечетную функцию |
T периодически на всю вещественную ось. Для этого |
следует применить разложение в ряд Фурье по косинусам или по синусам,
соответственно.
П р и м е р. Зададим на интервале [0, ) функцию |
y x . |
Разложим функцию в ряд по косинусам с помощью MAXIM-ы. Для этого применим команду load(fourie); fourcos (x, x, %pi). Мы получим
коэффициенты |
a |
|
|
|
0 |
|
интервале |
( , ) |
|
и |
an = |
2(cos( n)-1) |
. График частной суммы ряда на |
2 |
|
n |
2 |
|
|
|
|
|
|
до |
|
10-го |
члена получим по команде plot2d(%pi/2+ |
sum((2*(cos(%pi*n)/n^2-1/n^2))/%pi*cos(n*x),n,1,10),[x,-%pi,%pi]).
4
fun1 x
3
2
1
0
-1
-2
-3
-4
x
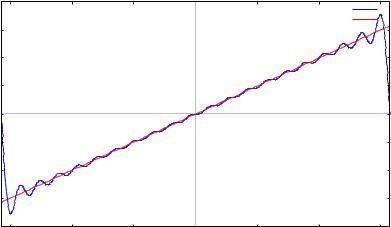
Здесь синяя линия – ряд Фурье по косинусам, красная – исходная функция.
Разложим функцию в ряд по синусам по команде load(fourie);
foursin(x,x,%pi). Коэффициенты ряда имеют вид
что частные суммы соответствующего ряда сходятся медленнее, чем частные
суммы |
в предыдущем случае. График частной суммы ряда на интервале |
( , ) |
до 20-го члена получим по команде plot2d(sum((2*(-cos(%pi*n)/n)) |
*sin(n*x),n,1,20),[x,-%pi,%pi]). |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
fun1 |
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
|
|
x |
|
|
|
Здесь синяя линия – ряд Фурье по синусам, красная – исходная функция.
Дифференциальные уравнения
Дифференциальным уравнением называется соотношение вида
. Решить дифференциальное уравнение – это
значит, определить функцию
, удовлетворяющее этому соотношению,
возможно, в неявном или параметрическом виде. |
|
|
Простейшее |
дифференциальное уравнение |
вида |
y (x) f (x) |
решали, так |
как находили y(x) f (x)dx . |
Мы |
знаем, что |
определяется с точностью до произвольного постоянного слагаемого. То есть решение простейшего дифференциального уравнения содержит произвольную постоянную. Решения более сложных дифференциальных уравнений также находятся с точностью до произвольных постоянных. Конкретная функция, удовлетворяющая дифференциальному уравнению, называется частным решением дифференциального уравнения. Множество всех частных решений называется общим решением дифференциального уравнения. Общее решение дифференциального уравнения содержит все произвольные константы, получающиеся вследствие интегрирования.
Порядок дифференциального уравнения определяется наивысшим порядком входящих в него производных. Поэтому дифференциальное
уравнение вида |
F(x, y(x), y , y ,..., y |
(n) |
) 0 |
считается дифференциальным |
|
уравнением n -го порядка.
Так же, как не любая функция может быть проинтегрирована, и представлена в виде элементарных функций, так и не любое дифференциальное уравнение имеет решение, выражающееся через элементарные функции. Класс дифференциальных уравнений, интегрируемых в квадратурах, узок. Мы изучим несколько классов дифференциальных уравнений, интегрируемых в квадратурах, а также рассмотрим некоторые приближенные методы решения дифференциальных уравнений. Кроме того, мы рассмотрим некоторые задачи, связанные с применением дифференциальных уравнений.
Дифференциальное уравнение первого порядка с разделяющимися переменными
Так называются уравнения вида
виде отношения дифференциалов:
выражения, содержащие |
x |
и |
f (x) g(y) . Запишем производную в
(x) g( y) и разнесем в разные части Мы получим равенство двух
|
дифференциалов: |
dy |
f (x) dx . После интегрирования правой части по x , |
|
g( y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а левой – по |
y мы получим слева функцию, зависящую от |
y , а справа – |
|
функцию, |
|
зависящую |
от |
x , |
отличающихся |
на |
константу: |
|
|
dy |
|
|
f (x) dx C . |
|
|
|
|
|
|
|
g( y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П р и м е р. В соответствии с законом радиоактивного распада вещества скорость распада пропорциональна количеству нераспавшегося вещества.
|
Если обозначить m(t) |
массу нераспавшегося вещества в момент |
t , |
то этот |
|
закон можно записать в виде соотношения: m (t) m . Знак |
минус |
|
указывает на то, что масса вещества убывает с ростом t . |
|
|
|
Решение. Разделим |
переменные: |
dm |
dt . После интегрирования |
|
m |
|
|
|
|
|
|
получим ln m t lnC . Здесь произвольное постоянное слагаемое мы представили в виде логарифма положительной постоянной величины для
t |
. |
удобства последующего потенцирования: m(t) Ce |
Проанализируем полученное решение. Оно содержит постоянные (эта постоянная зависит от вида радиоактивного вещества – стронций, радий, уран….) и С – постоянную интегрирования. Предположим, что мы
исследуем радиоактивный |
распад радия, для которого |
|
измерять время в годах. Решение уравнения распада имеет |
|
вид |
m(t) Ce |
0,02 t |
, и мы |
получаем множество решений |
|
присутствия произвольной положительной константы С .
Как выбрать единственное? В данном случае, чтобы узнать, какое количество радиоактивного вещества останется по прошествии определенного времени, необходимо знать, сколько его было в начальный
момент. Задавая m(0) |
, мы задаем значение С . Таким образом, чтобы решать |
конкретные задачи, процессы в которых описываются дифференциальными уравнениями, необходимо не только само уравнение, но и дополнительные данные, количество которых определяется порядком дифференциального уравнения. Для решения задачи, поставленной для дифференциального уравнения первого порядка, необходимо задать начальное условие y(t0 ) y0 . Уравнение вкупе с начальным условием называется задачей
Коши.
Однородное дифференциальное уравнение первого порядка
Так называют уравнение вида y F |
|
y |
|
. Для решения такого уравнения |
|
x |
|
|
|
|
целесообразно ввести новую функцию |
|
|
y(x) |
p(x) . Тогда |
y(x) xp(x) и |
|
|
|
|
|
|
|
x |
|
Подставляя |
в |
исходное |
уравнение, |
получим |
|
p(x) xp (x) F( p(x)) |
или |
p (x) |
F( p) p |
. Последнее уравнение |
|
x |
|
|
|
|
|
|
уравнение с разделяющимися переменными. |
Решив его и найдя p( |
|
найдем и y(x) xp(x) . |
|
|
|
|
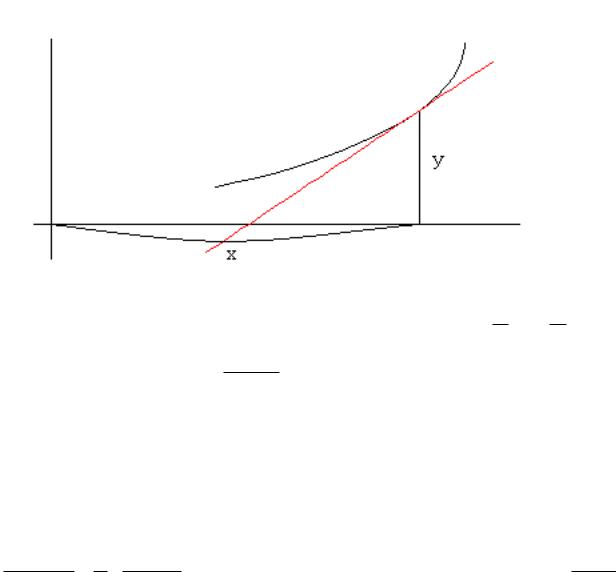
П р и м е р. Найти кривые, у которых точка пересечения любой касательной с осью абсцисс одинаково удалена от точки касания и от начала координат. Выбрать среди кривых ту, которая проходит через точку (2,1).
Решение. В соответствии с геометрическим условием |
(x |
y |
) |
2 |
( |
y |
) |
2 |
y |
2 |
. |
|
|
y |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
Упрощая, получим |
y |
|
2xy |
|
. |
Это |
однородное дифференциальное |
|
x |
2 |
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнение первого порядка. |
Вводя функцию p(x) , |
придем к уравнению с |
|
разделяющимися переменными |
|
|
xp |
p(1 p2 ) |
. |
Разделив переменные, |
|
|
|
|
1 p2 |
|
|
|
|
|
|
|
|
|
|
|
|
получим равенство
раскладывается на
|
(1 p |
2 |
) |
|
|
1 |
|
2 p |
|
|
|
|
|
|
|
|
|
p(1 p |
2 |
) |
p |
(1 p |
2 |
) |
|
|
|
|
|
|
|
|
|
дифференциалов |
(1 p2 )dp |
|
dx |
. Левая |
дробь |
|
p(1 p2 ) |
x |
|
|
|
|
|
|
|
|
простейшие |
дроби |
следующим |
образом: |
|
. В результате после интегрирования имеем |
x |
Cp |
, |
|
1 p |
|
|
|
|
|
|
|
|
2 |
|
и возвращаясь к старой функции по формуле y(x) xp(x) , получим
y C(x2 y2 ) . Семейство кривых мы построили. Теперь нужно выбрать ту кривую, которая проходит через точку (2,1). Подставляя координаты точки в
уравнение, получим
выбранной кривой:
. Таким образом, уравнение
Пример анализа решений дифференциального уравнения с разделяющимися переменными
Это пример связан с применением дифференциальных уравнений с разделяющимися переменными в экологии.
Логистическая кривая.
Рассмотрим уравнение роста популяции за счет размножения. Пусть какая-то популяция, например, популяция рыб, запущенных в пруд, растет вследствие хороших условий из-за естественного прироста количества особей. Первое время, пока рыб немного, скорость прироста пропорциональна количеству
рыб в водоеме. Если |
обозначить количество особей |
y(t) , то |
дифференциальным уравнением будет
, и значит, решением будет
экспоненциальная функция y(t) C e |
k t |
, где число |
C |
означает начальное |
|
количество рыб, а положительный |
коэффициент |
k |
отражает условия |
размножения рыб. Однако бесконечно количество особей увеличиваться не может вследствие ограниченности водоема, количества кислорода в нем и корма. При определенном количестве рыб начинаются болезни, кислородное голодание, и увеличивается смертность. Поэтому коэффициент k является не
числом, а функцией от |
y(t) , уменьшающейся при возрастании |
y(t) . |
Заменим дифференциальное уравнение роста популяции дифференциальным
уравнением |
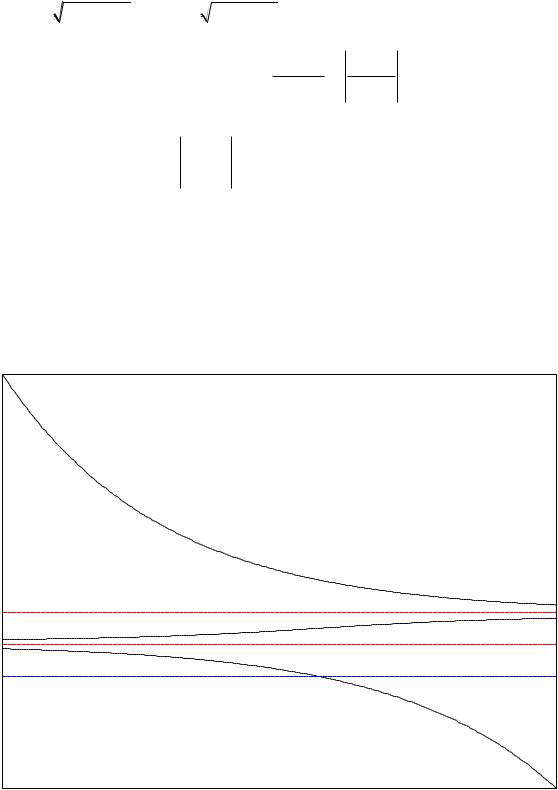
y (k a y) y . Решим это уравнение и получим неявную |
|
ln |
y(t) |
k t ln C |
|
| k a y(t) | |
|
|
|
. Очевидно, что при t имеем
|
(красная прямая) вне зависимости от знака разности |
k a y(t) . |
|
Если продифференцировать по переменной t |
обе части соотношения |
|
ln |
y(t) |
k t ln C , получим: |
y (t) |
|
0 . |
Это значит, что |
|
| k a y(t) | |
k a y(t) |
|
|
|
|
|
|
y(0) |
k |
, |
то соответствующее решение (логистическая кривая) возрастает к |
|
a |
|
|
|
|
|
|
|
значению |
k / a с ростом t , а если y(0) |
k |
, то логистическая кривая убывает |
|
a |
|
|
|
|
|
|
к значению k / a с ростом t .
Квоты отлова.
Продолжая тему исследования популяции рыб в водоеме, предположим, что во избежание вымирания лишних рыб следует отрегулировать регулярный отлов части рыбы. Предположим, что скорость отлова задана и равна b . Тогда дифференциальное уравнение примет вид y (k a y) y b .
Решая это уравнение с разделяющимися
|
соотношению |
|
|
|
2 |
dy |
|
|
dt . |
|
a( y |
y k / a b / a) |
|
|
|
|
|
|
|
|
|
|
|
|
переменными, придем к
Вид первообразной слева
зависит от дискриминанта квадратного трехчлена в знаменателе.
|
|
k |
2 |
b |
|
|
1. Пусть |
4 |
. Тогда общее решение дифференциального уравнения |
|
|
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
имеет вид: |
y(t) |
k |
|
(t C) |
ab k |
2 |
|
от |
|
2a |
tg |
|
/ 4 , и вне зависимости |
|
|
|
|
|
|
|
|
|
|
|
|
начального значения y(0) , связанного с выбором константы C , с ростом |
t |
|
значение y(t) будет |
уменьшаться, пока |
|
не примет значения 0. Таким |
|
образом, при квоте отлова |
b |
k 2 |
|
рыба в водоеме исчезнет независимо от |
|
4a |
|
|
|
|
|
|
|
|
|
|
того, сколько ее запустить вначале.
y |
k |
k |
2 |
4ab |
|
|
k |
k |
2 |
4ab |
|
,y |
|
|
|
|
|
|
|
|
|
1 |
|
2a |
2 |
|
|
2a |
|
|
|
|
|
. Поэтому решение дифференциального
|
|
|
|
|
|
|
|
|
|
|
1 |
|
y y |
a t C . Очевидно, что |
|
уравнения можно записать в виде |
|
|
ln |
1 |
|
y |
y |
y y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
2 |
|
|
|
|
|
при t имеем |
|
y(t) y2 . |
Возьмем производную по t от обеих частей |
|
|
1 |
|
|
|
y y |
a t |
C и |
|
|
y |
a . |
|
соотношения |
|
|
|
|
ln |
1 |
|
получим |
|
|
|
|
y y |
|
y y |
( y y )( y y ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
2 |
|
|
|
|
|
|
|
1 |
2 |
|
|
Это значит, что кривая, представляющая решение, убывает при |
y y |
и при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
y y , а при |
y y y |
кривая возрастает. |
|
|
|
|
|
|
1 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
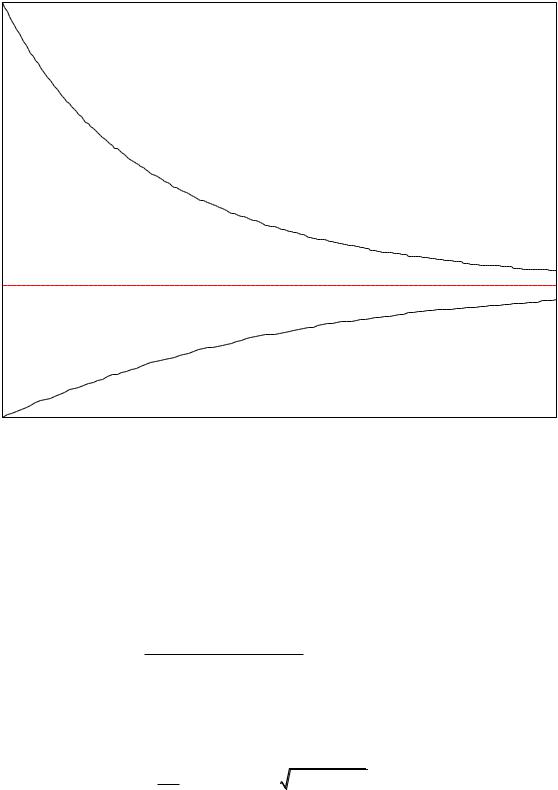
На соответствующем графике (в так называемой фазовой плоскости) прямые
y y , |
y y |
обозначены красным цветом. Прямая |
y 0 |
обозначена |
1 |
2 |
|
|
|
голубым цветом.
Уравнение в полных дифференциалах и приводимое к нему
Уравнение первого порядка
записано в виде |
M (x, y)dx N(x, y)dy 0 |
. Представим теперь, что |
M |
N |
|
y |
x |
и эти функции непрерывны. Это означает, что существует такая функция
U (x, y) |
, |
что |
U (x, y) M (x, y), |
U |
(x, y) N(x, y) |
. Действительно, ведь |
|
x |
(x, y) N |
y |
|
|
U (x, y) U |
(x, y) M |
(x, y) |
. Итак, уравнение теперь имеет вид |
xy |
|
yx |
y |
x |
|
|
U dx U dy 0 |
или |
dU (x, y) 0 |
. Следовательно, решение исходного |
x |
y |
|
|
уравнения – множество неявно заданных функций U (x, y) C . |
|
|
|
|
|
|
|
П р и м е р. |
Решить уравнение |
2xydx (x2 y2)dy 0 . |
Мы видим, |
|
что |
условие |
M N |
выполняется. Перегруппировывая слагаемые |
|
в |
виде |
|
|
y |
x |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
dy 0 , можно заметить, что первая скобка – это |
|
d(x |
2 |
y) . |
(2xydx x |
dy) y |
|
|
Следовательно, |
уравнение можно |
переписать в виде |
d(x2 y y3 / 3) 0 . |
Следовательно, решением является неявно заданная функция x |
2 |
y y |
3 |
/ 3 C . |
|
|
Иногда удается найти для произвольного дифференциального уравнения
вида |
M (x, y)dx N(x, y)dy 0 |
такую функцию |
(x, y) , что умножив обе |
части уравнения на эту функцию, мы превращаем его в уравнение в полных дифференциалах, так как ( M )y ( N)x . Такой сомножитель называется
интегрирующим множителем.
П р и м е р. Решить уравнение (x2 y2 x)dx ydy 0. Сгруппируем члены уравнения следующим образом: (x2 y2 )dx (xdx ydy) 0. Мы видим, что вторая скобка представляет собой d(x2 y2 )/ 2 . Разделим обе части
|
уравнение на первую скобку: |
dx |
d(x2 |
y2 ) |
0 или |
|
2(x2 |
y2 ) |
|
|
|
|
Отсюда |
x ln(x |
2 |
y |
2 |
) |
C . Здесь интегрирующим множителем явилась |
|
|
|
|
|
|
|
1/ 2 |
|
функция |
|
|
1 |
|
|
|
|
. |
|
|
|
(x |
2 |
y |
2 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Линейное дифференциальное уравнение первого порядка
Так называется дифференциальное уравнение вида y a(x)y b(x) . Здесь
сама функция и ее производная связаны линейно. Решать уравнение будем методом вариации произвольной постоянной. Для этого сначала решим соответствующее уравнение с нулевым свободным членом, называемое