Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ITIS0

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

3.31 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1611 12 13 14 15 16 > Следующая >>>

Пусть

| x | | x |

тогда | c x

| M

. Так как ряд

сходится, то по

k 1

теореме сравнения абсолютно сходится ряд c x1 .

k 0

Так как

расходится, то

c x

не может сходиться ни при каких

c x2

k 0

значениях x, | x | | x2 | , так как в противном случае он бы сходился, в

соответствии с доказанной частью теоремы, и при

x x2 .

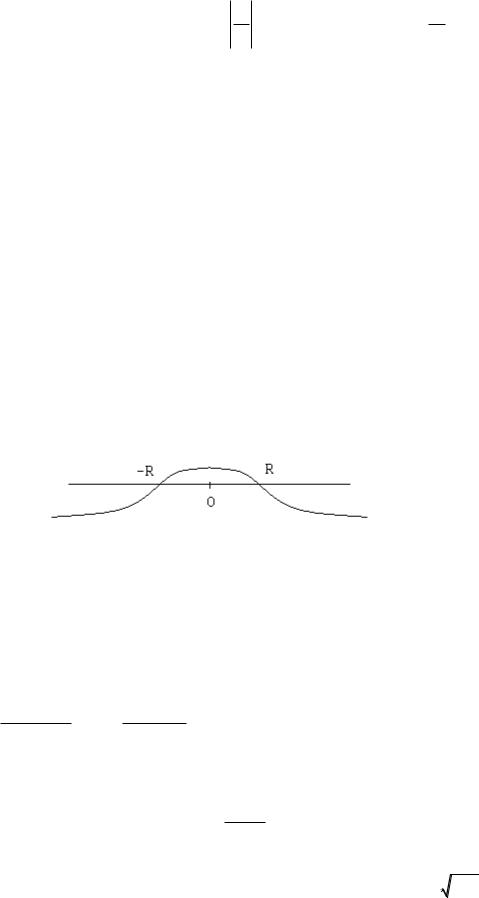
Из теоремы Абеля следует, в частности, что область сходимости степенного


ряда	c x	k	представляет собой некоторый интервал ( R, R) , а	область
ряда	c x		представляет собой некоторый интервал ( R, R) , а	область
	k
	k 0
расходимости – внешность этого интервала. Что касается двух точек				x R ,

являющихся границами этого интервала, то сходимость или расходимость ряда в этих точках следует проверять для каждой функции индивидуально.

Число	R	называется радиусом сходимости степенного ряда.
( R, R)	называется интервалом сходимости степенного ряда.

Способы определения радиуса сходимости степенного ряда

Интервал

lim n

то

соответствии

n 1

lim

| c

|| x |

n 1

то

| c

| c x

ряд

| ck xk |

расходится.

k 0


признаком		Даламбера			если
				\| cn 1 \|\| x \|
\| c xk \|	сходится, если		lim			1,

k			n		\| cn \|
k 0
Следовательно,		при	\| x \| R		имеем:

	\| c	\| R		R lim	\| c	\|
lim	n 1		1 или		n			.
lim	\| cn \|		1 или		n 1		\|	.
n	\| cn \|				n 1
n				n \| c

2. Аналогично используя признак Коши, получим R		1		.
2. Аналогично используя признак Коши, получим R				.
	lim n \| c \|
	n		n
	n

П р и м е р 1. Найти область сходимости степенного ряда

n 1

. Следовательно, R lim

(n 1)

радиус сходимости. Здесь c

Проверим сходимость в точке

x 1. Имеем ряд

p , который

n 1

если p 1 и расходится, если

p 1.

. Найдем

сходится,

		( 1)		n
Проверим сходимость в точке x 1. Имеем ряд		( 1)		, который сходится,
Проверим сходимость в точке x 1. Имеем ряд		n	p	, который сходится,
	n 1	n
	n 1
если p 0 и расходится, если	p 0 .

Замечание. Внутри интервала сходимости ряд можно почленно интегрировать и дифференцировать любое число раз. Это значит, что если


k	k	s
c x		s
k 0
2) (s(x))
		(m)

(x),		\| x

	k
		c
	k m

| (x

R , то
)		,
k	(m)

	b			b
			k			k
1)		s(x)dx	c		x		dx,
	a		k 0	a
\| x \| R .

| a |,| b |

Связь между коэффициентами степенного ряда и его суммой

Итак, пусть c x

s(x),

| x | R . Положим x 0 , тогда получим:

s(0) .

k 0

k 1

Возьмем производную от членов ряда и его суммы: c kx

s (x),

| x | R,

x 0 .

k 1

и положим

Тогда

s (0) . Продолжая процесс дифференцирования,

получим: n!cn s

(n)

(0) .

(n)

(0)

То есть,

Таким образом, коэффициенты

степенного ряда

являются коэффициентами формулы Тейлора для суммы ряда.

Поставим

вопросы: если

для произвольной

функции

f (x) ,

имеющей

(k )

(0)

бесконечное число производных в точке x 0

построить ряд

k !

k 0

называемый рядом Тейлора функции f (x) , то 1) где он будет сходиться, и

2) если будет сходиться, то будет ли сходиться к самой функции f (x) ?

Ответы на поставленные вопросы.

		f
1) Так как ряд Тейлора		f
1) Так как ряд Тейлора
	k 0

образом можно находить

(k ) k

(0)	x	k	– это степенной ряд, то для него обычным

!

радиус и интервал сходимости. То есть,

R lim |

f (n) (0) | (n 1) .

f (n 1) (0) |

2) Так как частная сумма ряда Тейлора – это полином из формулы

Тейлора

(k )

(0)

, то разность между частной суммой и функцией

f (x)

согласно

k !

k 0

формуле Тейлора есть остаточный член формулы Тейлора.

Мы его

rn (x)

(n)

( x)

рассматривали в форме Лагранжа:

, 0 1 .

Таким

образом, если внутри интервала сходимости остаточный

член формулы

Тейлора стремится к нулю с ростом n , то сумма ряда		Тейлора совпадает с
исходной функцией, по которой построен ряд. И	тогда	говорят, что
функция f (x) представима в виде ряда Тейлора,	то есть

f(x)

k 0

(k )
(0)	x	k
		k
k !
k !

Примеры разложения функций в ряды Тейлора

Пример 1. Рассмотрим функцию e

ex 1 1!x x2!2 x3!3 xnn! rn

x . В соответствии с формулой Тейлора

x ,

где \| r (x)\| emax{x,0}	\| x \|n 1	.

n	(n 1)!

Сосчитаем радиус сходимости степенного ряда.

R lim (n 1)! lim(n 1) .

n n! n

Таким образом, этот ряд сходится во всех точках вещественной оси.

Для того, чтобы выяснить,

будет ли сходиться ряд

к функции

k 0

n 1

заметим, что при любом значении

|x|

| x |

x R имеем | rn(x)| e

(n 1)!

n . Следовательно, e

при всех x R .

k 0

Пример 2. Рассмотрим функцию

f x sin x . В соответствии с формулой

Тейлора

e	x	,

при

sin

где

x	1	x
	1!

| rn (x) |

1	x	3


3!
	2n 1
\| x \|
(2n 1)!

1	x	5
	x

5!

. То есть,

		1 n 1
			x2n 1 r

			n
	2n 1 !
R lim			(2n 1)!
			(2n 1)!
		n

x ,

и rn(x) 0

при

Следовательно,

		1 n 1
sin x			x	2n 1


n 1	2n 1 !

при всех

x R

Пример 3. Рассмотрим функцию

Тейлора

cos x 1

f x cos x.


	1 n	x	2n	r
2n !		x		r

				n
				n

В соответствии с формулой

x ,

где

	2(n 1)
\| r (x)\|	\| x\|
n	(2n 2)!
	(2n 2)!

То есть,

	R lim	(2n 2)!
		(2n)!
	n

и rn(x) 0

при

n . Следовательно,


		1 n		2n
cos x	2n !		x	2n
cos x			x
n 0

при всех x R .

Пример 4. Рассмотрим функцию f x ln(1 x). В соответствии с формулой Тейлора

ln(1 x) x	x2		x3	... ( 1)n 1 xn r (x),

2		3		n	n

(n 1)

где

| rn(x)|

| x|

, 0 1.

Сосчитаем радиус сходимости

(n 1)

(n 1) |1 x |

этого

ряда: R lim

n 1

1. Форма Лагранжа остаточного члена

здесь

(n 1)

годится только для

x 0

. В этом случае

| rn(x)|

| x|

, и для

x 1

имеем rn(x) 0

при

n . Другая форма остаточного члена для

0 x 1 приводит к подобному результату. Поэтому для | x | 1

справедливо представление

	( 1)	n 1	x	n
ln(1 x)				.
	n
n 1

Пример 5. Рассмотрим функцию

формулой

	,
f x (1 x)

В соответствии с

Тейлора

(1 x)

1 x	( 1)	x	2	...	(
1 x		x		...

	2!

1)(

2)...( n!

n 1)

x	n

rn (x)

Найдем радиус сходимости этого степенного ряда: R lim	n 1	1.

n n

Для оценки остаточного члена при n , больших или равных целой части

форма Лагранжа остаточного члена годится также только для

случае имеем оценку:	\| rn(x)\|	\| ( 1)( 2)...( n) \|	(n 1)	.
		(n 1)!	\| x \|

0 . В этом

Очевидно,

что при значений

| x | 1

0 x 1

имеем

rn(x) 0

при

n . Для отрицательных

x применяем другую форму остаточного члена. В результате для справедливо представление

(1 x)

	( 1)( 2)...( n 1)
1	( 1)( 2)...( n 1)	x
		n
n 1	n!
n 1

Легко заметить, что полученная формула есть бесконечный аналог формулы

бинома Ньютона.

sin t t

Примеры приложений рядов Тейлора
Представленные в предыдущем пункте канонические разложения могут
служить основой для получения новых разложений. Так, положив 1	и
в последнем разложении, мы получим формулы суммы бесконечной

геометрической	прогрессии			со	знаменателем	( q) :
1 q q2 ... ( q)n ...		1	. Заменив в этой формуле q на ( q) , получим:
1 q q2 ... ( q)n ...		1 q	. Заменив в этой формуле q на ( q) , получим:
		1 q

1 q q			2	...		q			n	...		1	.
			2						n		1 q


Заменим в последней формуле q на t														2	, мы получим разложение
														2
1
1	2				( t	2	)	n	,	\| t \| 1		. Последний ряд имеет радиус сходимости, равный 1.
1 t						2		n

		n 0
		n 0
Вспомним, что внутри интервала сходимости ряды можно интегрировать
почленно и проинтегрируем обе части последнего равенства по t																от 0 до

| x | 1,

тогда получим разложение:


arctg x ( 1)	n
arctg x ( 1)
n 0

x	2n 1

2n 1

Выше, там, где мы говорили о функциях, не имеющих первообразной,

выраженной через элементарные функции, был приведен пример функции

. Благодаря простому разложению этой функции в ряд Тейлора, ее

можно проинтегрировать			по отрезку [0, x] и получить новую		функцию,
называемую			интегральным		синусом:
x sin t			x2k 1
Si(x) t	dt ( 1)k			.
		(2k 1)!(2k 1)
0	k 0

Формула Эйлера

Разложения функций

x	,	sin x
e

cos

в ряды Тейлора, справедливые для

всех

вещественных

, оказываются такими же и в случае, когда

комплексное

число.

Пусть

x i t ,

где

–

мнимая

единица, а

i t

в ряд Тейлора:

вещественное число. Разложим e

i t

1 i t

..... (1

...)

x t

–

i(t	t	3	t	5	t	7	....) cost	i sin t.

	3!		5!		7!

Вот эта формула, выражающая связь между ex , sin x комплексных переменных, и называется формулой Эйлера.

cos

в случае

Тригонометрические ряды Фурье

В различных отраслях науки, в том числе, в физике приходится иметь дело с периодическими явлениями. Простейший пример – электрические колебания.

Периодической называется функция							f (x)	,	для которой существует такая
величина	T ,	называемая периодом,					что		f (x) f (x T ) . Простейшими
T периодическими				функциями		являются			тригонометрические функции
вида sin	2 kx	,cos	2 kx		, где k –	целое число, называемые гармониками.
	T			T

Представление периодической функции в виде суммы гармоник называется гармоническим анализом. В случае, когда такая сумма бесконечна, мы получаем тригонометрический ряд, называемый рядом Фурье.

Итак, пусть непрерывная

периодическая функция

f (x)

представлена в

		a						2 kx			2 kx
	f (x)	a		a				2 kx		b sin	2 kx
виде тригонометрического ряда:	f (x)	0		a			cos			b sin
		2		k 1		k			T	k	T
		2							T		T
							k N
Возникает вопрос: как найти коэффициенты a			,a		,b	,	k N		?
		0		k	k

Воспользуемся тем, что гармоники обладают следующим свойством:

T / 2

cos 2 kx dx T

sin	2 kx	dx
	T

cos 2 lx sin

0 ,

2 mxdx 0, l,m N , T

T / 2

2 lx

2 mx

cos

dx 0, l,m N, l m

T / 2

2 lx

2 mx

sin

dx 0,

l,m N, l m ,

T / 2

2 lx

cos

T / 2

2 lx

sin

T / 2

Теперь для того, чтобы, например, найти am умножим обе части равенства

2 kx

2 mx

f (x)

cos

b sin

на

cos

и проинтегрируем на

k 1

отрезке [ T / 2,T / 2]

. С учетом свойств гармоник в правой части равенства

останется

только

слагаемое

в левой

части – выражение

T / 2

2 mx

f (x)cos

dx . Отсюда мы получим

am .

T / 2

Умножая на sin	2 mx			и интегрируя, получим bm .
Умножая на sin		T		и интегрируя, получим bm .
		T
А для того, чтобы получить					a , нужно просто проинтегрировать
					0
		a0
равенства f (x)		a0	ak cos 2 kx bk sin			2 kx на отрезке [ T / 2,
равенства f (x)			ak cos 2 kx bk sin			2 kx на отрезке [ T / 2,
	2			k 1	T	T
				k 1

обе части

T / 2].

Таким образом, непрерывная периодическая функция виде следующего тригонометрического ряда Фурье:

2 kx bk sin 2 kx

f (x)

ak cos

k 1

T / 2

2 kx

f (x)cos

dx,

k 0,1,2,....,

T / 2

2 kx

f (x)sin

dx,

k 1,2,....

T / 2

f (x)

представима в

где

Заметим, что

коэффициенты отрезке [ T2 ,T2

в случае,	когда	f (x)	четная на	отрезке	[ T	,T	] ,
					2	2
при синусах	обратятся в		ноль. Если	f (x) нечетная на

], исчезнут коэффициенты при косинусах и свободный член.

В случае, когда периодическая функция имеет точки разрыва, ее также можно раскладывать в ряд Фурье, но равенство функции и суммы ряда будет только в точках непрерывности функции. В точках разрыва ряд Фурье будет сходиться к полусумме значений функции слева и справа от точки разрыва:

a0			2 kx0	b sin	2 kx0	1		0) f (x 0)) .
	a	cos					( f (x
2			T		T	2
	k			k			0	0

k 1

Возможно разложение функции в ряд Фурье с помощью MAXIMы. Мы получим все коэффициенты ряда Фурье для функции f (x) , заданной на

отрезке

[ T,T ]

-периодически продолженной на всю вещественную ось,

если введем load(fourie); fourier(f(x),x,t) и нажмем Shift+Enter.

р.

Получим

коэффициенты

ряда Фурье для

функции

, x .

Для

этого

введем load(fourie); fourier(%e^x,x,%pi),

f (x) e

нажмем Shift+Enter и получим

- e

) /

nsin n /(n

(nsin n /(e

) e

)

cos n /(n

1)) / ,

cos n /(e n

sin n /(n

(sin n /(e

)

n cos n /(n

1)) / .

ncos n /(e

) e

Мы

видим,

что

коэффициенты

содержат

выражения

sin n 0 и

cos n ( 1)

. Поэтому преобразуем коэффициенты:

e e

( 1)n

(

e (n2 1)

(n2 1)

( 1)n n

(

e (n2

(n2 1)

Для того, чтобы не только вычислить коэффициенты ряда Фурье, но и

получить разложение функции

f (x) , заданной на отрезке

[ T,T ]

T –

периодически продолженной на всю вещественную ось в ряд Фурье, следует ввести load(fourie); totalfourier (f(x),x,T) и нажать Shift+Enter.

П р и м е р. Для разложения в ряд Фурье функции из предыдущего примера введем load(fourie); totalfourier (%e^x, x, %pi). При этом получим разложение

n( 1)

sin nx

( 1)

cos nx

1)(e

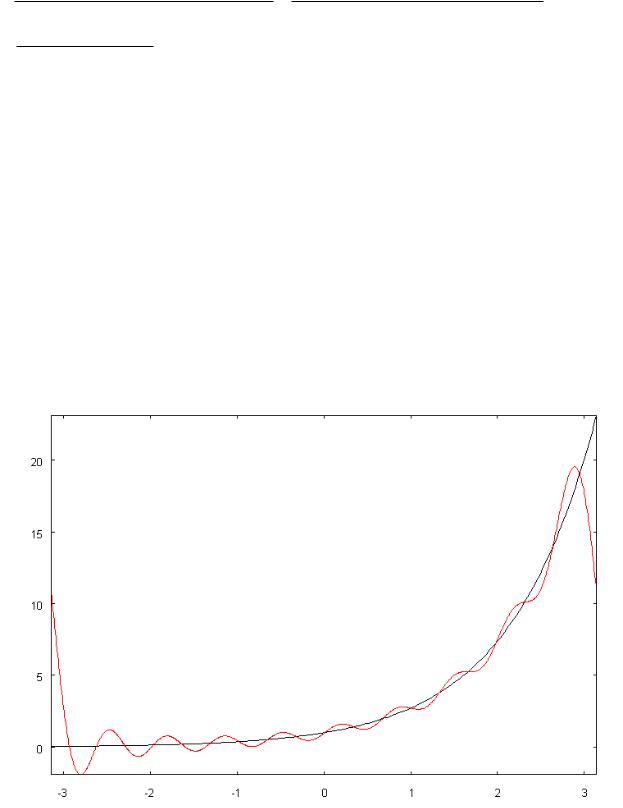
Следует отметить, что частные суммы ряда Фурье приближают исходную функцию не в конкретных точках, а «в среднем по отрезку». Сравним

заданную функцию	x	, - x , и 9-ю частную сумму ряда Фурье на
	y e

одном графике. Для этого сначала введем функцию g(x) , совпадающую с 9-й

частной суммой, а затем нарисуем функцию e	x	(черным цветом) и функцию

g(x) (красным цветом) на одном графике над отрезком [ , ]:

g(x):=-(%e^(-%pi)*(%e^%pi-1)*(%e^%pi+1)*sum((n*(- 1)^n*sin(n*x))/(n^2+1),n,1,9))/%pi+(%e^(-%pi)*(%e^%pi- 1)*(%e^%pi+1)*sum(((-1)^n*cos(n*x))/(n^2+1),n,1,9))/%pi+ (%e^(-%pi)*(%e^%pi-1)*(%e^%pi+1))/(2*%pi);

load(draw); draw2d(explicit(%e^x,x,-%pi,%pi), color=red, explicit(g(x),x,- %pi,%pi)).

В результате получим картину

Здесь видно, что в конечных точках	отрезка, где функция	y ex , - x ,
при периодическом продолжении	с отрезка [- , ]	в другие точки

вещественной оси терпит разрыв, график частной суммы ряда Фурье (красная линия) значительно отличается от графика экспоненциальной

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1611 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.202570.66 Кб0istoria_zad_otv.doc
#
03.08.2019189.95 Кб14Istoria_zarubezhnoy_literatury_18_veka.doc
#
01.03.202593.11 Кб0Istorii_tamozhennogo_dela_i_tamozhennoy_politik...docx
#
10.02.2015587.33 Кб41istoriya_i_filosofiya_nauki.pdf
#
01.04.202529.52 Кб1ISTORIYa_PEDAGOGIKI_OZO_PSIKh_OBRAZOV.docx
#
10.02.20153.31 Mб21ITIS0.pdf
#
22.04.2019744.45 Кб11itogovaya_baza_testov_po_GMU.doc
#
01.04.2025123.9 Кб0itog_test.doc
#
14.08.20194.53 Mб34ivashkevich_v_b_buhgalterskiy_upravlencheskiy_u...doc
#
22.08.201979.36 Кб6IVF_-_KK_-_Glava_III_-_UDEL_N_J_PERIOD_ROSSIJSK...doc
#
22.08.2019115.2 Кб3IVF_-_KK_-_Glava_IV_-_MOSKOVSKIJ_PERIOD_ROSSIJS...doc