Диплом / 4.4. Расчет для адаптив

4.3 Расчет оптимальных параметров настройки адаптивной системы автоматического регулирования

В теории автоматического управления разработаны различные методы расчета АСР при заданных критериях качества, а так же методы оценки качества переходных процессов при заданных параметрах объекта и регулятора. При этом на ряду с точными методами, требующих большие затрат времени и ручного труда разработаны приближенные методы позволяющие сравнительно быстро оценить рабочие параметры регулятора или качество переходных процессов (метод Циглера – Никольса для расчета настроек регуляторов; приближенные формулы для оценки интегрального квадратичного критерия и т.п.).

При определении настроек регуляторов в качестве показателя оптимальности системы регулирования обычно выбирают интегральный критерий качества (например, интегральный квадратичный критерий) при действии на объект наиболее тяже­лого возмущения с учетом добавочного ограничения на запас устойчивости системы. В практических расчетах запас устойчивости удобно характеризовать показателем колебательности системы; его значение для систем, имеющих интегральную составляющую в законе регулирования, определяется максимумом амплитудно-частотной характеристики замкнутой системы регулирования.

В дальнейшем под оптимальными будем понимать настройки регулятора, обеспечивающие заданную степень колебательности m процесса регулирования при минимуме интегрального квадратичного критерия J_кв.

Среди инженерных методов расчета настроек регуляторов одни являются более точными, но трудоемкими для ручного счета, другие – простыми, но приближенными. Наиболее распространенными способами, отражающими методику точного и приближенного расчета настроек, яв­ляются метод расширенных амплитудно-фазовых частотных характеристик (РАФЧХ) и метод незатухающих колебаний (Циглера – Никольса).

Метод незатухающих колебаний (Циглера—Никольса). В соответствии с этим методом расчет настроек ПИ- или ПИД-регуляторов проводят в два этапа: 1—расчет критической настройки пропорциональной составляющей S₁^кр(S₀ = S₂ = 0), при которой АСР будет находиться на границе устойчивости, и соответствующей ей _кр; 2 – определение по S₁^кр и _кр оптимальных настроек S₁*, S₀*, S₂*, обеспечивающих степень затухания   0,8 – 0,9.

Уравнения для расчета S₁^кр и соответствующей ей частоты при т = 0:

_об() +  = 0; S₁^кр = [A_об(_кр)] ^–1.

Оптимальные настройки ПИ- и ПИД-регуляторов находят по следующим формулам:

для П-регулятора

S₁* = 0,5S₁^кр

для ПИ-регулятора

S₁* = 0,45S₁^кр;

S₀*/S₁* = 0,19_кр или S₀* = 0,086S₁^кр_кр;

для ПИД-регулятора

S₁* = 0,6S₁^кр;

S₀*/S₁* = 0,32_кр или S₀* = 0,192S₁^кр_кр;

S₂*/S₁* = 0,785/_кр или S₂* = 0,471S₁^кр/_кр;

Метод Циглера – Никольса лежит в основе многих методов настройки дискретных ПИД-регуляторов. В частности, если рекуррентный алгоритм управления, соответствующий аналоговому ПИД-закону, имеет вид

,

то для больших значений периода квантования t₀ параметры настройки K₁*, K₀*, K₂* могут быть найдены по следующим формулам:

для П-регулятора

K₁* = 0,5 K₁^кр;

для ПИ-регулятора

K₁* = 0,45 K₁^кр – 0,5 K₀*;

K₀* = 0,54 K₁^крt₀/T_кр, если   0,25t₀;

для ПИД-регулятора

K₁* = 0,6 K₁^кр – 0,5 K₀*;

K₀* = 1,2 K₁^крt₀/T_кр, если   0,25t₀;

K₂* = 3/40 K₁^кр T_кр/t₀.

В приведенных уравнениях K₁^кр и T_кр – коэффициент при П-составляющей закона управления и период колебаний выходной координаты, соответствующие режиму незатухающих колебаний АСР.

Опишем процесс самонастройки в созданной модели адаптивной системы автоматического управления.

Первый этап. Все переключатели находятся в первом положении. В регуляторе устанавливаются настройки, гарантирующие устойчивость замкнутой системы с двумя заграждающими фильтрами: К_р = 0,7; Т_и = 60 с. В генераторы синусоидальных колебаний Г₁, Г₂ вводятся начальные значения амплитуд а₁, а₂ и периодов Р₁, Р₂ колебаний. Нормированный период колебаний низкочастотного генератора Г₁ был принят Р₁ = 28, а генератора Г₂ – соответственно вдвое меньше, т.е. Р₂ = 14. Амплитуда генератора Г₁ а₁ = 5%, а генератора Г₂ выбрана вдвое больше, т.е. а₂ = 10%. Таким образом, генератор Г₁ является ведущим, а Г₂ – ведомым, для которого двукратное соотношение амплитуд и частот сохраняется на протяжении всего этапа работы системы.

Сигнал задания для блоков фазовой автоподстройки частоты с помощью переключателя П₅ устанавливается в соответствии с методом Циглера – Никольса на уровне Ф_з = –.

После проведения таких подготовительных операций в работу включается генераторы синусоидальных колебаний, и блок фазовой автоподстройки частоты путем изменения нормированного периода колебаний Р₁ начинает отслеживать заданный фазовый сдвиг.

В конце первого этапа для нормированных периодов колебаний Р₁ = 36 и Р₂ = 18 установившееся значение фазового сдвига и амплитуды для низкочастотной составляющей в сигнале у₁ приняли следующие значения: Ф_б = –3,146 рад, А_б = 4,2453% и соответственно Ф₀ = –4,2 рад, А₀ = 3,859% для высокочастотной составляющей в сигнале у.

По этим значениям с помощью вычислительного блока 1 рассчитывается поправочный коэффициент С = А_ба₂/(А₀а₁) и требуемые по методу Циглера – Никольса настройки ПИ-регулятора:

К_р = 0,45а₁/А_б; Т_и = Р₁/0,5.

В данном случае С = 2,2; К_р = 0,53; Т_и = 72. Таким образом, критерием окончания первого этапа является достижение фазой Ф_б установившегося значения, близкого к –.

Второй этап. По команде блока управления проводятся следующие операции: вычисленные настройки вводятся в регулятор Р; поправочный коэффициент С запоминается в ЗУ₁; отключается низкочастотный генератор Г₁ и синхронный детектор СД₁; в высокочастотном генераторе Г₂ сохраняются нормированный период и амплитуда, соответствующая концу первого этапа; в ЗУ₂ запоминается значение фазового сдвига в ОУ; все переключатели устанавливаются в положение 2. Система продолжает работу, непрерывно удерживая с помощью синхронного детектора СД₂ и блока ФАЧ значение фазового сдвига на уровне Ф₀ = –4,2 рад на повышенной частоте пробных колебаний. Настройки регулятора корректируются периодически, через каждые два периода колебаний генератора. Расчет настроек на этом этапе производится по формулам:

К_р = 0,45а₂/(А₀С); Т_и = Р₂/0,25.

Отсюда видно, что наличие поправочного коэффициента позволяет оставаться на требуемом уровне.

Построим переходные процессы по каналам задающего воздействия (рис. 37) и возмущения, идущего со стороны регулирующего органа (рис. 38). Переходные процессы построены при настройках регулятора обеспечивающих устойчивость замкнутой системы (t < 700 c) и при настройках полученных в процессе адаптации (t  700 c).

h(t), ^oC

t, c

Рис. 37. Переходный процесс в адаптивной системе автоматического регулирования по каналу задающего воздействия

t, c

h(t), ^oC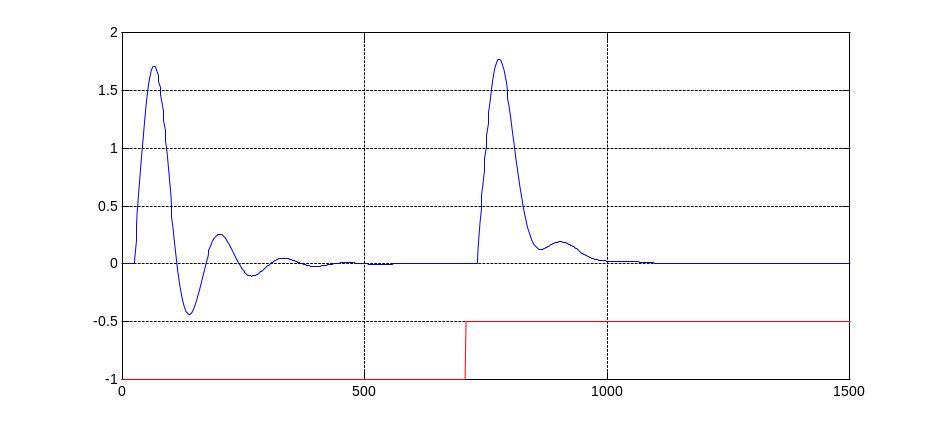

Рис. 38. Переходный процесс в адаптивной системе автоматического регулирования по каналу возмущения, идущего со стороны регулирующего органа

Оценим качество переходного процесса полученного после процесса адаптации.

Перерегулирование:

 = A₃/A₁100% = 18,5%.

Время регулирования:

t_p = 203 c.

Максимальная динамическая ошибка:

А₁ = 0,32

Степень затухания:

 = (A₁ – A₂)/A₁  0,95.

Следует заметить, что при изменении коэффициента усиления объекта поправочный коэффициент С остается постоянным. Необходимость повторения первого этапа с целью уточнения значения коэффициента С возникает только при значительных (в 2 раза и более) изменениях постоянных времени и запаздывания в объекте (табл. 7). В этой таблице приведены значения параметров настройки ПИ-регулятора по методу Циглера – Никольса для объекта управления при двукратном изменении относительно номинала (97,7 с) его постоянной времени Т (48,85 и 195,4 с) и значения параметров настройки при тех же вариациях постоянной времени Т на втором этапе самонастройки при фиксированном значении поправочного коэффициента С = 2,2.

Как видно из табл. 7 уход настроек от расчетных значений весьма незначительный и составляет не более 16% по коэффициенту усиления регулятора.

Таблица 7

Значения параметров настройки регулятора при вариации параметров объекта управления

Постоянная времени Т, с	Значения параметров настройки по методу Циглера – Никольса		Значения параметров настройки на втором этапе
	Кр	Ти	Кр	Ти
48,85	0,295	67	0,362	69,1
195,4	1,014	75,83	1,12	72,5

7